[人工智能]（CVPR-2021）具有深度通用线性嵌入的跨视角步态识别

具有深度通用线性嵌入的跨视角步态识别

paper题目：Cross-View Gait Recognition with Deep Universal Linear Embeddings

paper是北航发表在CVPR 2021的工作

论文地址：链接

Abstract

与指纹和虹膜等其他生物特征标识符相比，步态因其非侵入性和非合作特性而被认为是一种有吸引力的生物特征标识符。目前，跨视图步态识别方法总是从各种深度卷积网络中建立表示进行识别，而忽略了步态序列的潜在动态信息。如果假设行人具有不同的步行模式，则可以通过计算每个视角的动态特征来执行步态识别。本文将Koopman算子理论引入步态识别，可以为非线性动力系统的全局线性逼近找到嵌入空间。此外，提出了一种基于卷积变分自编码器和深度 Koopman 嵌入的新框架来逼近 Koopman 算子，将其用作来自线性化嵌入空间的动态特征，用于跨视角步态识别。它为步态识别系统提供了可靠的物理解释性。在大型公共数据集 OU-MVLP 上进行的实验证明了所提出方法的有效性。

1. Introduction

步态识别旨在通过识别人的体型和行走方式来识别人。与指纹或虹膜等其他生物特征相比，步态不需要检测目标合作，并且可以在更远的距离上执行。此外，它也很难伪装。因此，步态识别可以应用于一些特殊的事务，例如刑事调查。

尽管进展令人鼓舞，但步态识别仍然受到许多外部因素的影响，例如携带条件、不同的步幅、服装和相机视角，这些因素会降低步态识别系统的性能。在所有这些挑战因素中，相机视角可能是最棘手的一个。现有技术证明，如果改变视角，单视图步态识别系统的性能将急剧下降。

为了解决这些问题，已经提出了许多用于跨视角步态识别的深度学习模型，并取得了很好的效果。一般来说，这些方法可以分为两类，分别是基于外观的方法和基于模型的方法。前者是过去几年步态识别的主流。这些方法从步态轮廓图像中提取特征，并通过度量学习损失函数优化特征空间中的个体内距离，而无需步态周期建模。此外，还提出了时间融合单元和部分分割单元来结合轮廓序列和局部部分的特征。

基于模型的步态识别专注于以数学方式从步态序列重建身体结构。三维模型比二维模型传达更多信息，并且可以构建来表示步态模式。因此，它可以在理论上针对视角变化实现可接受的性能。一些生物力学步态分析也支持这一点。然而，这些方法的性能容易受到姿态估计的准确性和轮廓序列质量的影响，这限制了它们的发展。

一般来说，基于外观的方法擅长特征表示，但存在数据不足的问题，而基于模型的方法更能观察差异，但难以构建。尽管深度卷积神经网络 (ConvNets) 可以提供强大的特征提取器并在受控场景中实现出色的性能，但现有模型仍然不能很好地处理较大的视角差异或服装和物品携带的变化。因为，本质上，ConvNet 还是一个二维模板，而人体是一个三维对象。毫不奇怪，即使有确切的人的数据，该模型仍然无法处理他/她未包含在训练集中的 2D 投影。这个问题也被称为计算机视觉的不适定问题。

受基于惯性传感器的步态分析、生物力学步态分析和人类步态动态分析工作的启发，作者意识到动态特征在步态识别中具有竞争力，因为它模拟了人类步态的本质，运动过程，而不是纯粹的人形。因此，与大多数现有的深度学习方法不同，本文从动态系统的角度探索跨视角步态识别。更具体地说，作者介绍了 Koopman 理论，它是流体力学文献中分析非线性系统的流行工具。事实上，Koopman 理论已经作为视频背景分离、图像欺诈和运动检测应用于计算机视觉。至于步态识别，最相关的工作是 Wang 等人的工作[39]，其中应用窗口动态模式分解来生成步态能量图像。然而，在他们的工作中只研究了静态步态特征。

如图 1 所示，Koopman 理论侧重于非线性系统的系统线性表示，它提供了一种表示步态步行周期的新方法。通过近似 Koopman 算子提出了一种新的跨视角步态识别框架（见图 2）。首先，对齐的轮廓被输入卷积变分自动编码器 (VAE) 以进行图像级编码。然后，强制执行额外的约束和损失函数来识别动态线性演变的 Koopman 算子。最后，从 Koopman 矩阵中训练一个全连接的网络以获得最终的步态表示。

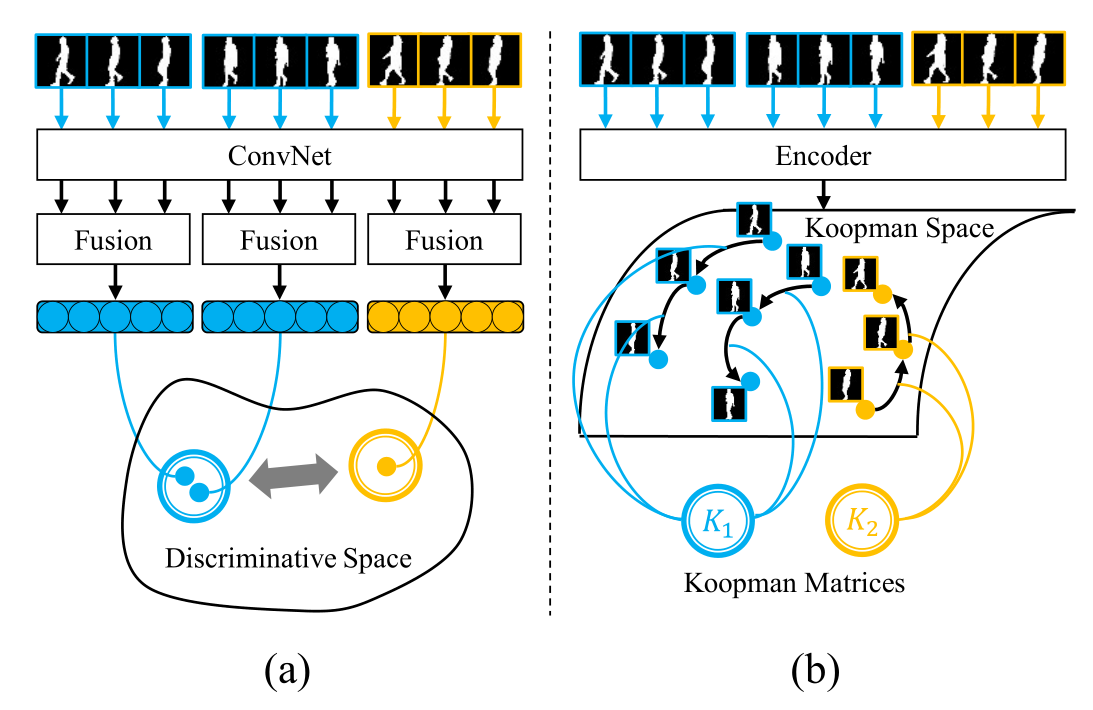
图 1. 以前的工作侧重于步态轮廓序列的特征融合，并搜索具有相同身份的特征对的距离较小的判别空间 (a)。本文计算步态图像线性演化的 Koopman 空间中的动态特征（b），然后从它们的动态特征中识别它们。

总而言之，作者做出以下三个主要贡献。

• 将 Koopman 理论引入步态轮廓的动态特征提取。这是第一项应用 Koopman 分析的研究。
• 通过集成卷积变分自动编码器和深度 Koopman 嵌入，提出了一种用于跨视角步态识别的新框架。
• 在广泛使用的大型步态数据库OU-MVLP上进行了实验。结果证明了本文方法的有效性，这对理解步态识别和人类步行动力学之间的联系做出了重要贡献。

2. Related Work

在本节中，将简要介绍最近在步态识别方面的工作。在深度学习时代之前，时间序列分析方法被应用于一些工作中，例如自回归建模和隐马尔可夫模式，用于动态建模。这些模型通常具有很强的假设，但它们也不能很好地拟合非线性系统。在深度学习时代，ConvNets已在众多计算机视觉任务中被证明是成功的，它也被用于步态识别并取得了令人钦佩的性能。一般来说，基于 ConvNet 的方法可以分为两类，基于外观的方法和基于模型的方法。同时，根据输入数据的类型，所提出的工作也可以分为基于模板的方法和基于序列的方法。

大多数基于模板的方法应用 ConvNets 从单个步态图像中提取步态特征，例如步态能量图像 (GEI)或其他类似 GEI 的模板图像。吴等人[43]提出了三个具有不同架构的 ConvNet，并进行了一系列实验，显着提高了跨视角步态识别性能。同时，还提出了一些生成模型来将步态图像从一个视图转换到另一个视角，例如自动编码器和生成对抗网络。

一些工作直接从步态轮廓序列建立模型。他们应用时间模型对信息进行跨时间编码，例如特征图池化、长短期记忆和三维ConvNet。一些关于大型步态数据库的最新作品呈现出具有竞争力的性能。GaitSet提出了一种将步态视为一组轮廓而不是连续序列的新颖观点。他们认为剪影的外观包含位置信息，这是对时间信息的替代。因此，他们应用一个简单的 ConvNet 从轮廓中提取帧级步态特征，然后使用池化操作将帧级特征聚合为单个集合级特征。张等人[50]提出了一种与 ConvNets 相结合的模型，用于单图像特征提取和 LSTM 注意力模型，用于帧级 ConvNet 上的注意力分数。GaitPart提出了一种带有微动作捕捉模块的新型基于部分的模型，该模型还提供了一种时间建模方法。

最近，一些工作专注于基于模型的步态识别方法。他们从步态图像序列中重建人体的数学结构。可以构建人体行走的三维数据，它比二维数据传达的信息更多。因此，它可以通过三维模型旋转来解决跨视角问题。然而，它收到过多的细节的影响，从而降低了crossview步态识别的性能。

3. The Koopman Operators

本节将介绍 Koopman 算子和扩展动态模式分解的基础知识。 Koopman 算子是一种线性但无限维的算子，通过数据驱动的方法进行近似。对于非线性动力系统，Koopman 观察函数将原始状态空间映射到一个嵌入空间，在该嵌入空间中，动力学将普遍线性发展。扩展动态模态分解 (EDMD) 是一种逼近 Koopman 特征值、特征函数和模态元组的方法。 EDMD 过程需要两个先决条件：快照数据集和观察函数字典。

给定一个离散时间动态系统，$x_t\in \mathcal{M}$在时间步$t$，描述为：
$$x_{t+1}=F\left(x_t\right)$$
其中$F$表示及时映射系统状态的动力学。 Koopman 理论根据函数的演化提供了对动力系统的另一种描述，即 Koopman 算子$\mathcal{K}$，它是一个无限维线性算子。将特征函数表示为${\phi }_p:\mathcal{M}\to \mathcal{F}$和Koopman算子$\mathcal{K}$的特征值${\lambda }_p$，有
$$\mathcal{K}{\phi }_p\left(x_t\right)={\lambda }_p{\phi }_p\left(x_t\right),p=1,2,\dots$$
考虑一个向量值函数$g:\mathcal{M}\to \mathcal{F}$。$\mathcal{K}$将$g$映射到一个新函数$\mathcal{K}g$中，满足：
$$\mathcal{K}g\left(x_t\right)=g\left(F\left(x_t\right)\right)$$
如果$g$位于特征函数${\phi }_p$的范围内，则$g$可以根据特征函数展开为
$$g\left(x_t\right)=\sum _{p=1}^{\infty }{\phi }_p\left(x_t\right)v_p$$
然后有
$$\begin{array}{rl}g\left(F\left(x_t\right)\right)& =\mathcal{K}g\left(x_t\right)\\ & =\sum _{p=1}^{\infty }\mathcal{K}{\phi }_p\left(x_t\right)v_p\\ & =\sum _{p=1}^{\infty }{\lambda }_p{\phi }_p\left(x_t\right)v_p\end{array}$$
因此，如果将${\lambda }_p$视为系数，则系统的动态是线性的：
$$g\left(F\left(x_t\right)\right)=Kg\left(x_t\right)$$
其中 Koopman 算子$\mathcal{K}$将产生一个矩阵$K$到由${\phi }_p$跨越的子空间。传统上，观测函数$g$可以通过手工设计的方法从基础物理知识中确定。然后，系统识别问题可以转化为求 Koopman 矩阵$K$，在给定收集到的数值数据的情况下，可以通过线性回归求解。总之，Koopman 算子理论侧重于非线性系统的线性表示，捕获原始非线性系统的全部信息。

4. Proposed Approach

4.1. Problem Formulation

给定一个步态轮廓序列，可以将其视为时间序列数据 { x t } \left\{x_{t}\right\} {xt?}，其中$t\in [1,2,\dots ,M]$，$M$是该步态序列中的帧数。 Koopman 理论表明，通过在线性空间中用 Koopman 算子表示非线性动力学系统，可以将线性系统的预测用于系统状态分析。假设通过假设行人具有独特的步行模式，将人类步行视为动态系统。在这种情况下，可以根据受试者$i$的步态轮廓序列 { x i , t } \left\{x_{i, t}\right\} {xi,t?}计算不同的 Koopman 矩阵$K_i$：
$$g\left(x_{i,t+1}\right)=K_{i}g\left(x_{i,t}\right)$$
一旦可以通过最小二乘解从 { x i , t } \left\{x_{i, t}\right\} {xi,t?}估计$K_i$，可以在比较估计的步行模式${\hat{K}}_i$的相似性后识别行人的身份：
K ^ i T = L S ( Φ ( { x i , t } ) ) \hat{K}_{i}^{\mathrm{T}}=L S\left(\Phi\left(\left\{x_{i, t}\right\}\right)\right) K^iT?=LS(Φ({xi,t?}))
其中$\Phi$是表示观察函数$g$的卷积神经网络，$LS$代表最小二乘解。因此，将步态识别任务制定如下：
?feat? i = Ψ ( L S ( Φ ( { x i , t } ) ) ) \text { feat }_{i}=\Psi\left(L S\left(\Phi\left(\left\{x_{i, t}\right\}\right)\right)\right) ?feat?i?=Ψ(LS(Φ({xi,t?})))
其中$\Psi$是一个全连接网络，它将估计的 Koopman 矩阵${\hat{K}}_i$转换为用于个体识别的判别空间中的新特征。

此外，估计的 Koopman 矩阵${\hat{K}}_i$也可用于预测未来，因为它包含原始系统的信息。在我们的模型中，行人$\left\{{\tilde{\hat{x}}}_{i,t}\right\}$的未来图像可以预测为：
$${\tilde{\hat{x}}}_{i,t+T}={\hat{K}}_i^T\Phi \left(x_{i,t}\right)$$

4.2. Model Architecture

模型由三个关键组件组成，包括观察函数逼近模块 (OFA)、Koopman 矩阵记忆 (KMM) 和判别特征提取器模块 (DFE)。

在 OFA 模块中，应用具有卷积层的变分自动编码器 (VAE)来利用深度学习的能力来表示 Koopman 算子的特征函数。 KMM 模块包含训练集中每个人的可学习参数 Ki，可以通过反向传播进行训练。在 DFE 模块中，使用简单的全连接网络将估计的 Koopman 矩阵转换为用于跨视角识别的判别空间。该模型如图 2 所示。

图 2. 提出的方法的框架。在训练步骤一中，OFA 和 KMM 模块被训练。在训练步骤二中，只有 DFE 模块中的参数使用 OFA 中的参数进行训练。

Observation Functions Approximating

在观察函数逼近模块中，输入数据是对齐的步态轮廓序列。在时间步长$t$具有身份$i$的图像$x_{i,t}$被输入编码器$\Phi$，
$$z_{i,t}=\Phi \left(x_{i,t}\right)$$

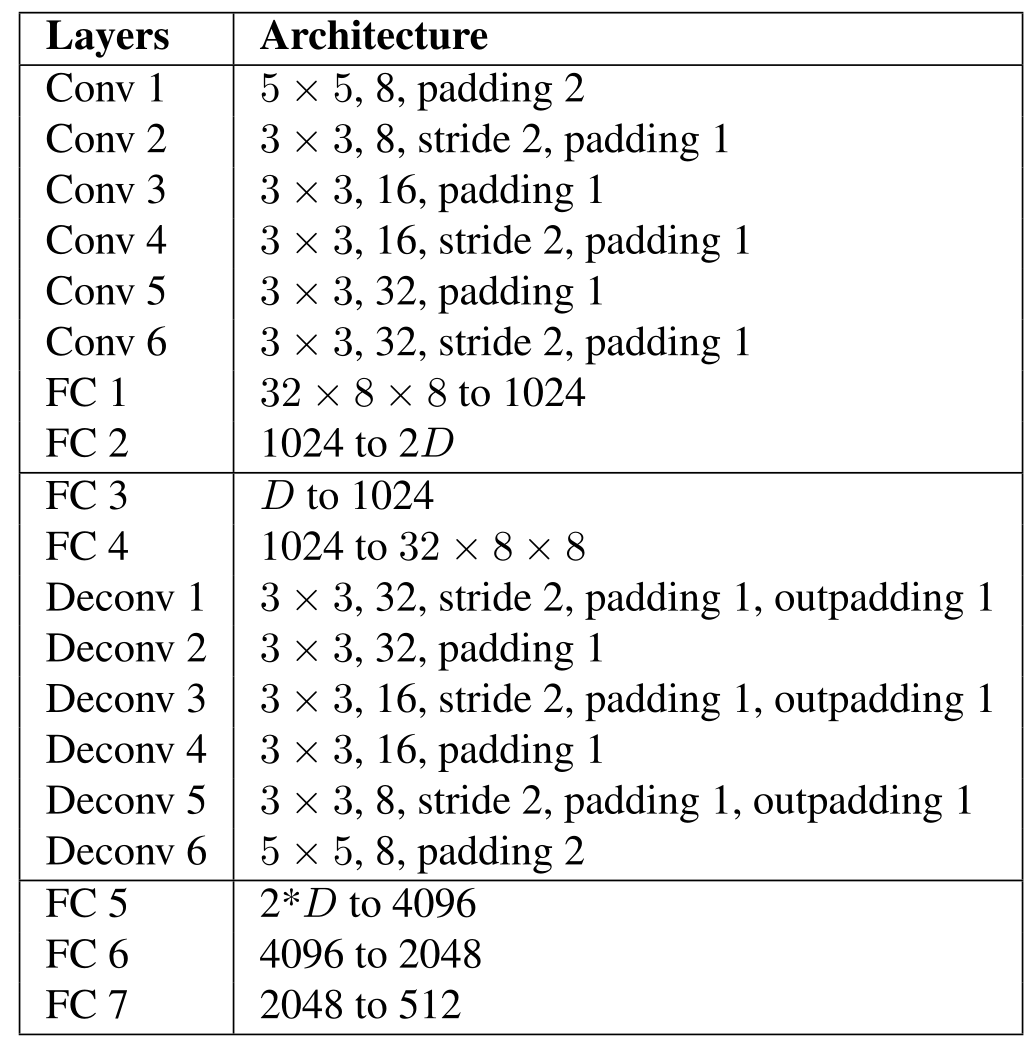
编码器$\Phi$包含六个卷积层和两个全连接层，如表1所示。在全连接层之后，网络给出一个平均向量$\mu$和一个标准差向量$\sigma$。他们都是$D$维的。然后得到从分布$N\left(\mu ,{\sigma }^2\right)$中采样的$x_{i,t}$的编码。编码器$\Phi$旨在借助深度网络的非线性变换而不是原始观察函数将原始输入数据$x_{i,t}\in {\mathbb{R}}^n$转换为 Koopman 空间$z_{i,t}\in \mathcal{F}$。$\Phi$的输出大小为$D$，这意味着在这项工作中，设置$\mathcal{F}={\mathbb{R}}^D$。$D$是该模型的超参数，可以通过实验确定。在这项工作中，设置$D=128$。认为 128 维空间足以逼近 Koopman 矩阵进行识别，因为步态周期是一个相对简单的动力系统。

一个解码器${\Phi }^{?1}$用于确保 Koopman 空间中的代码$z_{i,t}$保留原始图像中的大部分有用信息，而不是收敛于诸如零之类的异常值，而架构也显示在表 1 中，
$${\tilde{x}}_{i,t}={\Phi }^{?1}\left(z_{i,t}\right)$$

该编码器-解码器模块通过将原始步态序列转换为 Koopman 空间来提取人类行走模式。代替手工设计的观察函数，编码器-解码器结构能够表示任意函数，包括所需的 Koopman 特征函数。因此，本文的模型可以准确地拟合人类步行动力学，而无需手动设计功能。

表 1. 编码器$\Phi$、解码器${\Phi }^{?1}$和全连接网络$\Psi$的架构。除了 FC 2 和 FC 7 之外，每个卷积和全连接层之后都会跳过激活函数 ReLU。FC 5 和 FC 6 之后的批量归一化层也被跳过。每个卷积层后面的字符串被格式化为过滤器的大小，即特征图的维度。 Conv 代表卷积算子，Deconv 代表 2D 转置卷积算子，而 outpadding 代表添加到输出形状一侧的附加尺寸。

Koopman Matrix Memory

假设个体具有独特的步行模式。因此，他们的 Koopman 矩阵在匀速行走时应该是相同的。为了在训练阶段实现这一假设，为训练数据集构建了一个 Koopman Matrix Memory$K$。 $K=\left[K_i\right]$是一个可学习的参数矩阵，通过反向传播从预测相同步态序列中的下一帧进行训练。训练集中的每个个体都有一个唯一的$K_i$，它是一个$D\times D$矩阵，随机初始化。在输入步态序列$X=\left[x_{i,t}\right]$被编码为$Z=\left[z_{i,t}\right]$后，$K_i$用于预测 Koopman 空间中下一个快照的状态
$$\left[{\hat{z}}_{i,2},{\hat{z}}_{i,3},\dots ,{\hat{z}}_{i,t+1}\right]=K_i\left[z_{i,1},z_{i,2},\dots ,z_{i,t}\right]$$

$K_i$直接从Koopman Matrix Memory$K$加载。这样可以保证不同视角的输入步态序列可以编码到同一个空间中。需要注意的是，Koopman Matrix Memory$K$仅用于训练 OFA 模块。 OFA 模块中的参数被冻结后，该 KMM 模块将从模型中移除，不再使用。

Discriminative Feature Extractor

最后，一个简单的全连接网络$\Psi$将估计的 Koopman 矩阵${\hat{K}}_i$转换为判别空间中的新特征：
$${\text{?feat?}}_i=\Psi \left({\hat{K}}_i\right)$$
其中欧几里得距离可以用来衡量两个特征的相似度。还应该注意的是，输入数据${\hat{K}}_i$是通过公式 K ^ i T = L S ( Φ ( { x i , t } ) ) \hat{K}_{i}^{\mathrm{T}}=L S\left(\Phi\left(\left\{x_{i, t}\right\}\right)\right) K^iT?=LS(Φ({xi,t?}))中所示的最小二乘估计计算的，而不是来自 Koopman Matrix Memory 的$K_i$。$\Psi$的架构如表 1 所示。

4.3. Loss Functions

实现了OFA模块中自编码器的重构精度，以减少空间信息丢失。 ${\mathcal{L}}_{\Phi }$是指原始步态轮廓序列与从线性空间恢复的步态轮廓序列之间的差异，如下：
$${\mathcal{L}}_{\Phi }=\Vert x_{i,t}?{\Phi }^{?1}\left(\Phi \left(x_{i,t}\right)\right)\Vert$$

同时，应用额外的损失${\mathcal{L}}_{\mu ,\sigma }$来增强模型生成能力，它试图将分布推向尽可能接近单位高斯，
$${\mathcal{L}}_{\mu ,{\sigma }^2}=KL\left(N\left(\mu ,{\sigma }^2\right)\Vert N(0,1)\right)$$
其中$KL$代表 Kullback-Leibler 散度。

根据 Koopman 理论，学习线性动力学$K_i$以确保线性动力学：$\Phi \left(x_{i,t+1}\right)=$ $K_i\Phi \left(x_{i,t}\right)$。更一般地说，在$S$个时间步上执行线性预测，损失为：
$${\mathcal{L}}_{\text{linear?}}=\Vert \Phi \left(x_{i,t+S}\right)?K_i^S\Phi \left(x_{i,t}\right)\Vert$$
此外，还需要在$S$个时间步长上使用${\mathcal{L}}_{\text{furure?}}$预测未来的步态图像：
$${\mathcal{L}}_{\text{furure?}}=\Vert x_{i,t+S}?{\Phi }^{?1}\left(K_i^S\Phi \left(x_t\right)\right)\Vert$$
在这些损失中，范数$\Vert ?\Vert$是均方误差，并且它们都是在训练批次中平均的。

至于 DFE 模块，带有硬挖掘的三元组损失${\mathcal{L}}_{\text{triplet?}}$和 Softmax 损失${\mathcal{L}}_{\text{softmax?}}$都用于身份识别。在一个训练批次中，从训练集中随机选择$p\times k$个步态轮廓序列，其中$p$表示所选主题的数量，$k$表示不同视角的数量。对于一个训练batch中的每一个数据作为anchor，为${\mathcal{L}}_{\text{triplet?}}$选择最难的正数据和最难的负数据。同时，对${\mathcal{L}}_{\text{softmax?}}$应用了一个额外的分类器，它以$y_i$作为输入，在图 2 中省略。

4.4. Implementation Details

在训练过程中，整个模型分两步训练。一起训练 OFA 和 KMM 模块，在训练步骤一中没有 DFE 模块。然后冻结 OFA 模块的参数，在第二步训练中单独训练 DFE 模块而不使用 KMM 模块。原因是最小二乘解应用于计算的 Koopman 矩阵${\hat{K}}_i$。如果完全训练这个模型，它需要通过最小二乘解中的特征分解步骤反向传播损失，这是不稳定的。此外，如果不能正确建立 Koopman 空间，则 Koopman 矩阵${\hat{K}}_i$都是无理数。因此，采用了两步训练策略。

在训练步骤一中，OFA 和 KMM 模块与损失函数一起训练：
$${\mathcal{L}}_{\text{step?}1}=\alpha {\mathcal{L}}_{\Phi }+\beta {\mathcal{L}}_{\mu ,{\sigma }^2}+\gamma {\mathcal{L}}_{\text{linear?}}+\lambda {\mathcal{L}}_{\text{furure?}}$$
在训练步骤二中，使用损失函数训练 DFE 模块：
$${\mathcal{L}}_{\text{step?}2}=\xi {\mathcal{L}}_{\text{triplet?}}+{\mathcal{L}}_{\text{softmax?}}$$
在步态轮廓序列的两个训练步骤中随机选择 32 个连续帧作为训练样本。在测试阶段，每 32 帧计算一个 Koopman 矩阵。因此，得到不止一个 Koopman 矩阵，因为步态序列中总是有超过 32 帧。probe样本和gallery样本之间的最终距离将是该探针序列的所有计算的 Koopman 矩阵的平均距离。

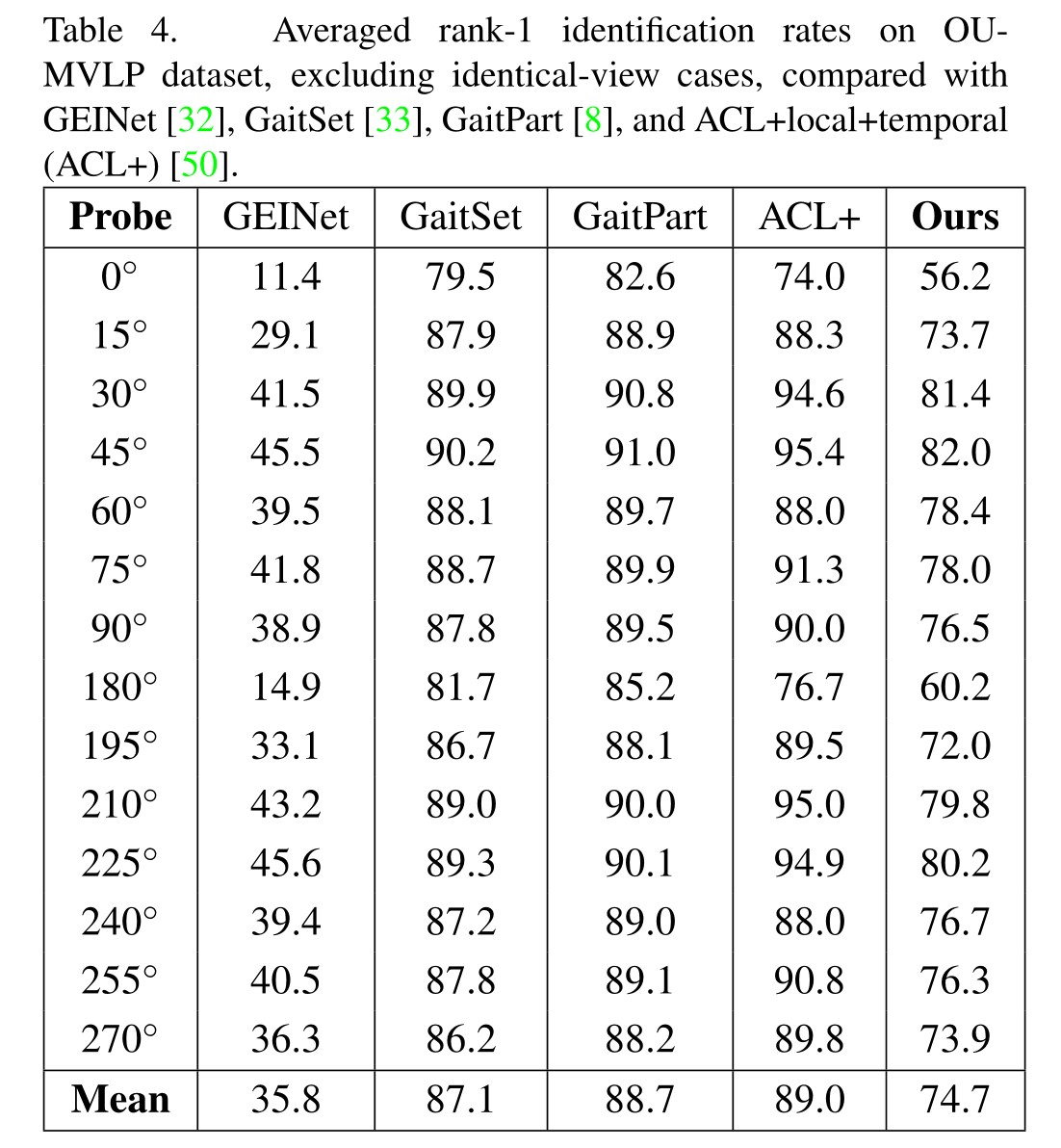
Results

参考文献

[39] Jiawei Wang, Edel B Garcia, Shiqi Y u, and Dexin Zhang. Windowed dmd for gait recognition under clothing and carrying condition variations. In Chinese Conference on Biometric Recognition, pages 484–492. 2017. 2

[43] Zifeng Wu, Y ongzhen Huang, Liang Wang, Xiaogang Wang, and Tieniu Tan. A comprehensive study on cross-view gait based human identification with deep cnns. IEEE transactions on pattern analysis and machine intelligence, 39(2):209–226, 2016. 1, 2, 7

[50] Y uqi Zhang, Y ongzhen Huang, Shiqi Y u, and Liang Wang. Cross-view gait recognition by discriminative feature learning. IEEE Transactions on Image Processing, 29:1001– 1015, 2019. 1, 3, 7, 8