积分图像(Integral image)
积分图算法由Crow在1984年首次提出,是为了在多尺度透视投影中提高渲染速度。积分图算法是一种快速计算图像区域和以及图像区域平方和的算法。它的核心思想就是对每一个图像建立起自己的积分图查找表,在图像处理的阶段就可以根据预先建立积分图查找表直接查找从而实现对均值卷积的线性时间计算。做到了卷积执行的时间与窗口大小无关。之前介绍的NL-means算法就可以采用积分图算法进行优化加速。
从直观来说,一张图像就是一个矩形,这个矩形中每个像素点的积分值,就是以图像左上角像素点为左上角顶点,以该像素点为右下角顶点的矩形中包含的所有元素之和。如下图所示,点(x,y)处的积分值为矩形区域中所有像素之和(包括该点)。
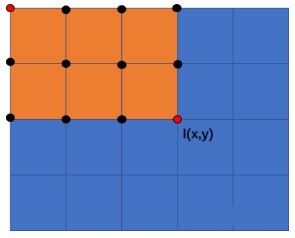
实际计算积分图的时候,为了提高计算效率,通常不会对每一个像素点都重新计算矩形区域包含的所有元素值之和,而是利用相邻点的积分值实现快速计算,如下图所示,点(x,y)的积分值可以使用点(x-1,y)与点(x,y-1)的积分值之和,然后减去重叠区域,也就是减去点(x-1,y-1)的积分值,最后再加上点(x,y)的像素值得到点(x,y)的积分值。
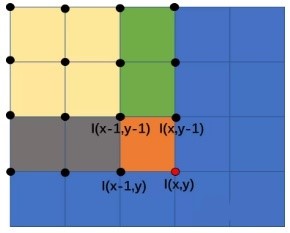
上述原理用公式表示为:
I(x,y) = I(x-1,y) + I(x,y-1) - I(x-1,y-1) + pixel(x,y)
此外还需要考虑边界问题,也就是第一行和第一列的计算。
对于第一行:
I(0,0) = pixel(0,0),x=0,y=0
I(x,0) = I(x-1,0) + pixel(x,0),x>0,y=0
对于第一列:
I(0,y) = I(0,y-1) + pixel(0,y),x=0,y>0
根据上述原理,基于OpenCV与C++的实现代码如下:
void Integral(Mat src, Mat &integal_out)
{
Mat tmp(src.size(), CV_64FC1, 0.0);
tmp.ptr<double>(0)[0] = (double)src.ptr<uchar>(0)[0];
for(int i = 1; i < src.cols; i++) //第一行
{
tmp.ptr<double>(0)[i] = tmp.ptr<double>(0)[i-1] + src.ptr<uchar>(0)[i];
}
for(int i = 1; i < src.rows; i++) //第一列
{
tmp.ptr<double>(i)[0] = tmp.ptr<double>(i-1)[0] + src.ptr<uchar>(i)[0];
}
for(int i = 1; i < src.rows; i++) //第i行
{
for(int j = 1; j < src.cols; j++) //第j列
{
tmp.ptr<double>(i)[j] = tmp.ptr<double>(i)[j-1] + tmp.ptr<double>(i-1)[j] - tmp.ptr<double>(i-1)[j-1] + src.ptr<uchar>(i)[j];
}
}
tmp.copyTo(integal_out);
}
参考OpenCV的官方文档:
C++: void integral(InputArray image, OutputArray sum, int sdepth=-1
Parameters:
image – Source image as W X H , 8-bit or floating-point (32f or 64f).
sum – Integral image as (W + 1) X (H + 1) ,
32-bit integer or floating-point (32f or 64f).
sdepth – Desired depth of the integral and the tilted integral images,
CV_32S, CV_32F, or CV_64F.
发现为了能容纳最后一列和最后一行的情况,最终的积分图就应该是 (W + 1) X (H + 1)大小,如下图所示,假设输入图像大小为2x2,则积分图大小为3x3:
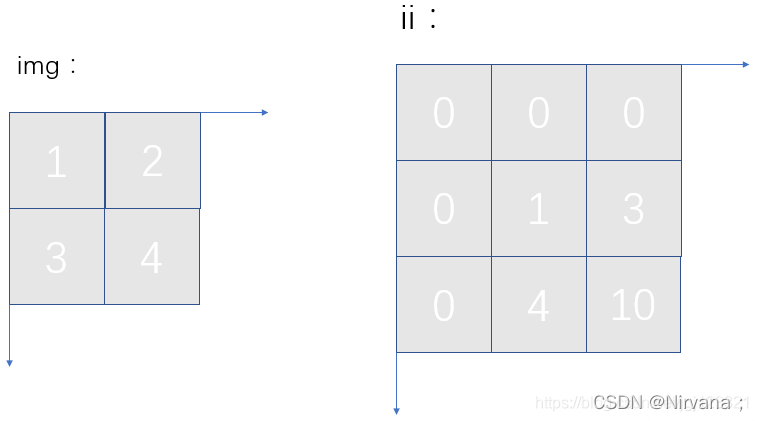
OpenCV官方提供两种积分图函数integral(),可以直接调用:
//API一
void integral( InputArray src, //输入图像
OutputArray sum, //和表
int sdepth = -1,); //和表深度
//API二
void integral( InputArray src, //输入图像
OutputArray sum, //和表
OutputArray sqsum, //平方和表
int sdepth = -1, //和表深度,一般为CV_32S
int sqdepth = -1 ); //平方和表深度,一般为CV_32F
OpenCV实现过程:
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int main() {
Mat src, sum, sqrsum;
src = imread("1.png", 0);
integral(src, sum, sqrsum, CV_32S, CV_32F);
normalize(sum, sum, 0, 255, NORM_MINMAX, CV_8UC1, Mat());
normalize(sqrsum, sqrsum, 0, 255, NORM_MINMAX, CV_8UC1, Mat());
imshow("原图", src);
imshow("和表积分图", sum);
imshow("平方和表积分图", sqrsum);
waitKey(0);
return 0;
}
我们还可以对兴趣区域(ROI)内的像素求和或者平方和:
#include <opencv2/opencv.hpp>
using namespace std;
using namespace cv;
int get_block_sum(Mat &sum, int x1, int y1, int x2, int y2);
int main() {
Mat src, sum, sqrsum;
src = imread("1.png", 0);
//获取ROI,便于观察(使用ImageWatch插件)
int LR = 4;
int LC = 4;
int width = 6;
int height = 6;
Mat roi = src(Rect(LR, LC, width, height)).clone();
//计算积分图
integral(src, sum, sqrsum, CV_32S, CV_32F);
//利用积分图计算ROI内的像素值总和
int value = get_block_sum(sum, LR, LC, LR + height, LC + width);
cout << value << endl;
imshow("原图", src);
waitKey(0);
return 0;
}
int get_block_sum(Mat &sum, int x1, int y1, int x2, int y2) {
int BottomRight = sum.at<int>(x2, y2);
int TopLeft = sum.at<int>(x1, y1);
int TopRight = sum.at<int>(x1, x2);
int BottomLeft = sum.at<int>(x2, y1);
int sum_value = (BottomRight + TopLeft - TopRight - BottomLeft);
return sum_value;
}