Simple moving average(SMA)
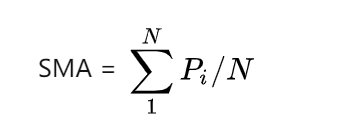
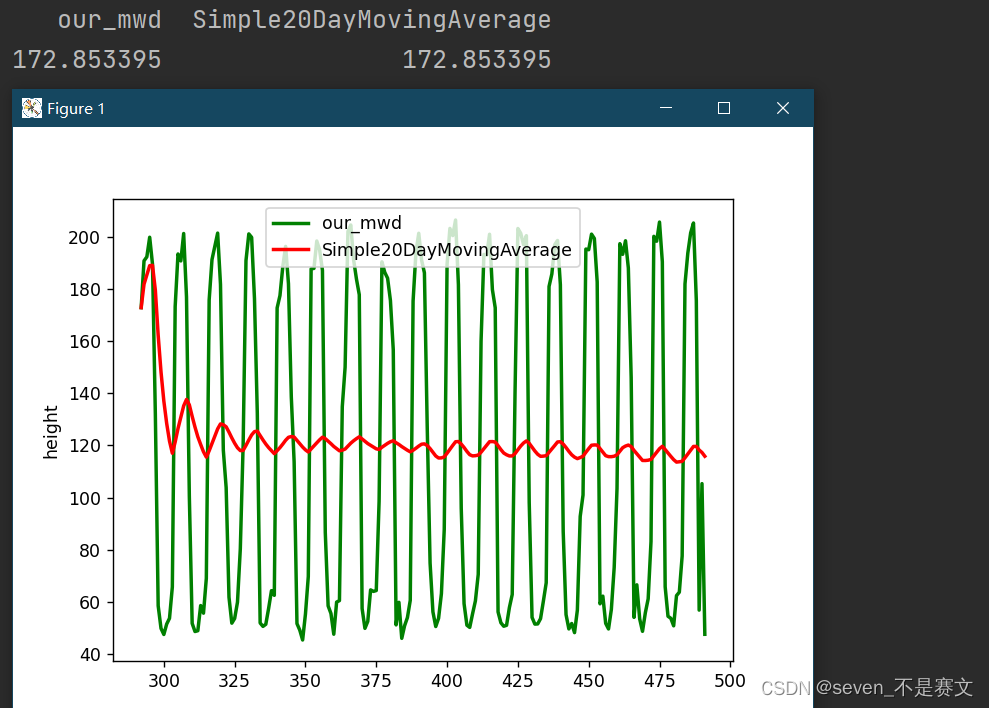
使用最近的50天分析,n=20
import numpy
import talib
import pandas as pd
import numpy as np
import os
import re
import statistics as stats
import csv
import pickle
import matplotlib.pyplot as plt
from math import sqrt
from sklearn.metrics import mean_squared_error
'预测模型:Simple moving average(SMA)简单易懂平均'
'我们把一段时间的价格加起来,除以这段时间的长度就可以得到。'
'简单移动平均的思想是,我们给于每一天同样的权值,'
'因为我们假设不管是离我们当前较近的日期,还是较远的日期,'
'对于我们当前价格的影响都是相同的。当我们的日期不断的往后走,'
'我们的『窗口』也在同时滑动,所以称之为移动平均。'
# input = numpy.random.random(50)
# print(input)
#
# # 默认计算30个值来平均一次
# output = talib.SMA(input)
# print(output)
# print(type(output)) #<class 'numpy.ndarray'>
# ...
data = pd.read_csv('mean_mwd.csv',header=0)
df = pd.DataFrame(data)
mwd = df['mwd']
with open("dict_data.pkl", 'wb') as fo: # 将数据写入pkl文件
pickle.dump(df, fo)
with open("dict_data.pkl", 'rb') as fo: # 读取pkl文件数据
dict_data = pickle.load(fo, encoding='bytes')
# print(dict_data.keys()) # 测试我们读取的文件
# print(dict_data)
a=dict_data.tail(492) #选择最近的492天的数据
close=a['mwd']
# print(close)
# print(a)
time_period = 100 # 移动平均的天数 ,那么只会取后面20天的数据
history = [] # 保存历史数据
sma_values = [] # 保存simple moving averages
for close_price in close:
history.append(close_price)
if len(history) > time_period: # 我们想我们历史数据中写入数据,只需保存20条,如果超过,就删除。
del (history[0])
sma_values.append(stats.mean(history))
#
a = a.assign(our_mwd=pd.Series(close, index=a.index))
a = a.assign(Simple20DayMovingAverage=pd.Series(sma_values, index=a.index))
close_price = a['our_mwd']
sma = a['Simple20DayMovingAverage']
# print(sma)
# print(a)
rmse = sqrt(mean_squared_error(mwd, sma))
print('Test RMSE: %.3f' % rmse)
fig = plt.figure()
ax1 = fig.add_subplot(111, ylabel='height')
close_price.plot(ax=ax1, color='g', lw=2., legend=True)
sma.plot(ax=ax1, color='r', lw=2., legend=True)
plt.show()
#一条是我们自己的数据线(绿色),另一条是sma曲线
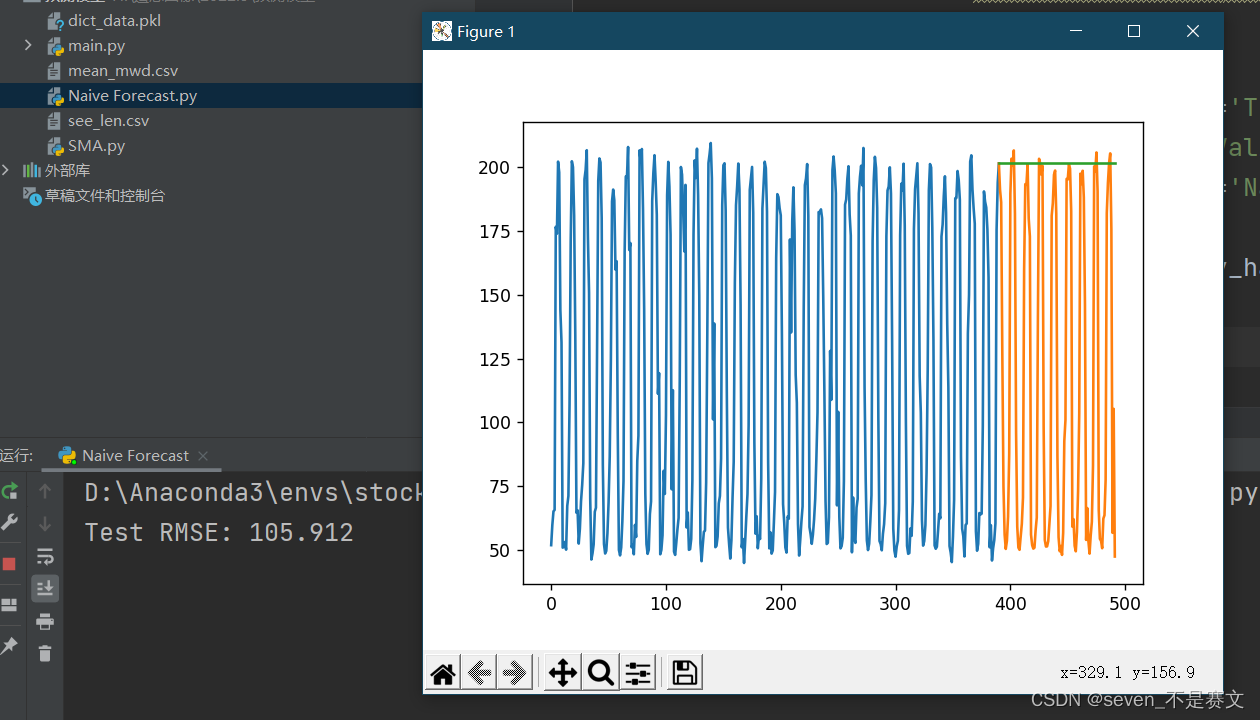
朴素法Naive Forecast
'''
如果数据集在一段时间内都很稳定,
我们想预测第二天的价格,可以取前面一天的价格,预测第二天的值。
这种假设第一个预测点和上一个观察点相等的预测方法就叫朴素预测法(Naive Forecast)
'''
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from math import sqrt
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.holtwinters import ExponentialSmoothing
train=pd.read_csv('mean_mwd.csv')
train['time'] = pd.to_datetime(train.time, format='%Y-%m-%d-%H-%M')
# print(train.dtypes)
# print(train.head())
# print(train.time.dt.year) #单独提取时间里面的年份
# print(train)
Train = train.loc[:390] #划分训练集和测试集
# print(Train)
# print(len(Train))
valid = train.loc[390:]
# print(valid)
dd = np.asarray(Train.mwd) #将结构数据转化为ndarray
y_hat = valid.copy() #复制一下
y_hat['naive'] = dd[len(dd)-1]
plt.plot(Train.index, Train['mwd'], label ='Train')
plt.plot(valid.index,valid['mwd'], label='Valid')
plt.plot(y_hat.index,y_hat['naive'], label='Naive Forecast')
rmse = sqrt(mean_squared_error(valid.mwd, y_hat.naive))
print('Test RMSE: %.3f' % rmse)
plt.show()
'''
霍尔特-温特(Holt-Winters)方法
在 Holt模型基础上引入了 Winters 周期项(也叫做季节项),
可以用来处理月度数据(周期 12)、季度数据(周期 4)、星期数据(周期 7)等时间序列中的固定周期的波动行为。
引入多个 Winters 项还可以处理多种周期并存的情况。
'''
y_hat_avg = valid.copy()
fit1=ExponentialSmoothing(np.asarray(Train['mwd']),seasonal_periods=7,trend='add',seasonal='add',).fit()
y_hat_avg['Holts_Winter'] = fit1.forecast(len(valid))
plt.plot( Train['mwd'], label='Train')
plt.plot(valid['mwd'], label='Valid')
plt.plot(y_hat_avg['Holts_Winter'], label='Holt_Winter')
rms = sqrt(mean_squared_error(valid.mwd, y_hat_avg.Holts_Winter))
print('Test RMSE: %.3f' % rmse)
plt.show()
蓝色部分为训练集数据,橙色部分为测试集部分。绿色的那条线就是这个朴素模型预测的结果
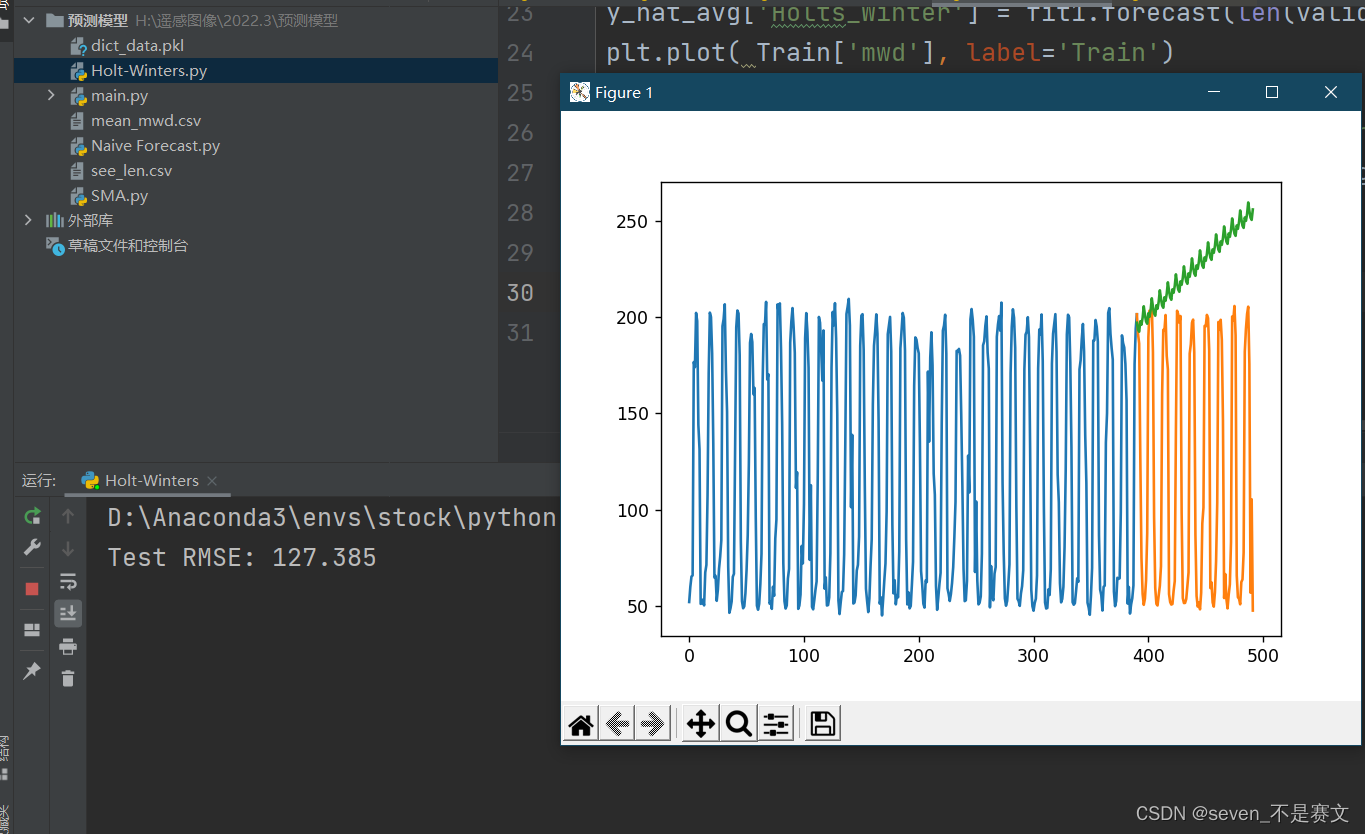
霍尔特-温特(Holt-Winters)
'''
霍尔特-温特(Holt-Winters)方法
在 Holt模型基础上引入了 Winters 周期项(也叫做季节项),
可以用来处理月度数据(周期 12)、季度数据(周期 4)、星期数据(周期 7)等时间序列中的固定周期的波动行为。
引入多个 Winters 项还可以处理多种周期并存的情况。
'''
import pandas as pd
import numpy as np
import matplotlib as mpl
import matplotlib.pyplot as plt
from math import sqrt
from sklearn.metrics import mean_squared_error
from statsmodels.tsa.holtwinters import ExponentialSmoothing
train=pd.read_csv('mean_mwd.csv')
train['time'] = pd.to_datetime(train.time, format='%Y-%m-%d-%H-%M')
# print(train.dtypes)
# print(train.head())
# print(train.time.dt.year) #单独提取时间里面的年份
# print(train)
Train = train.loc[:390] #划分训练集和测试集
# print(Train)
# print(len(Train))
valid = train.loc[390:]
# print(valid)
y_hat_avg = valid.copy()
fit1=ExponentialSmoothing(np.asarray(Train['mwd']),seasonal_periods=7,trend='add',seasonal='add',).fit()
y_hat_avg['Holts_Winter'] = fit1.forecast(len(valid))
plt.plot( Train['mwd'], label='Train')
plt.plot(valid['mwd'], label='Valid')
plt.plot(y_hat_avg['Holts_Winter'], label='Holt_Winter')
rmse = sqrt(mean_squared_error(valid.mwd, y_hat_avg.Holts_Winter))
print('Test RMSE: %.3f' % rmse)
plt.show()