[人工智能]论文理解 —— Prioritized Experience Replay

• 标题：Prioritized Experience Replay
• 文章链接：Curriculum Offline Imitating Learning
• 发表：ICLR 2016
• 领域：强化学习 —— Replay Buffer

• 摘要：经验重放允许 online RL agent 记住并重用过去的经验。在之前的工作中，经验 transition 是从 replay buffer 中统一取样的。然而，这种方法只是以 agent 实际执行 transition 的相同频率重放这些 transition，而不管其重要性如何。在本文中，我们开发了一个按优先次序重放经验 transition 的框架，以便更频繁地重放重要的 transition，从而更有效地学习。我们将优先经验重放与 DQN 相结合，在许多 Atari 游戏中实现了人类水平的性能，并达成了新的 SOTA，在49个游戏中有41个的表现优于使用均匀经验重放的 DQN

1. Replay Buffer 背景

• 不管算法细节，几乎所有 RL 算法都在做以下两件事
  
  1. 数据收集（for predict）：agent 与环境交互，收集 episode/transition 样本
  2. 学习过程（for control）：利用收集的样本更新策略，以最大化 return

1.1 On-policy 的问题

• 最早的 RL 算法同时做这两件事，于是得到了 on-policy 算法框架，其 agent 与环境交互的行为策略和最终学到的策略是相同的，如下所示
  
  举例来说，经典 on-policy 方法 sarsa 的数据流图如下
  

• 同时做两件事，就要同时处理价值估计面临的贡献度分配和策略更新面临的探索利用困境，这会导致几个问题

  1. 训练不稳定：要良好地估计价值函数，需要无限次地访问所有 $s$ 或 $(s,a)$，因此 agent 不得不把环境探索结合到其策略中，比如使用 $\epsilon$-greedy 策略，这不但增加了不稳定定性，且无法直接得到最优策略。更重要的是，on-policy 算法的探索是直接建立在其价值估计上的，而价值估计又来自探索经验，二者循环依赖，这会导致更强的风险寻求行为（比如某状态位置价值估计高了，就会进一步倾向于试探这附近的位置，有点正反馈的意味），使得训练不稳定
  2. 数据相关性强：由于我们使用轨迹中连续的 transition 作为训练样本，短期数据相关性是很强的（比如玩电子游戏，连续两帧画面之间非常相似），这违反了机器学习常见的 i.i.d 原则，在做梯度下降时，最近一段时间内的梯度方向总是相似，会导致更多震荡
  3. 数据利用率低：on-policy 要求必须使用当下行为策略采集的 transition 更新策略，因此过去的经验 transition 无法重用，所有数据用一次就扔掉了，有些当前不重要但后期重要的 transition 无法发挥最大作用，数据浪费严重

1.2 Off-policy 和 replay buffer

• 由于 on-policy 算法存在上述问题，人们提出了 off-policy 框架，将数据收集和策略提升两个任务解耦分别处理，其包含两个策略

  1. 行为策略behavior policy ${\pi }_b$：专门负责 transition 数据的获取，具有随机性因而可以无限次地采样所有 $s$ 或 $(s,a)$
  2. 目标策略target policy ${\pi }_t$：利用行为策略收集到的样本以及策略提升方法提升自身性能，并最终成为最优策略

  举例来说，经典的 off-policy 方法 Q-learning 使用 $\epsilon$-greedy 作为行为策略，使用 greedy 作为目标策略，其数据流图如下
  

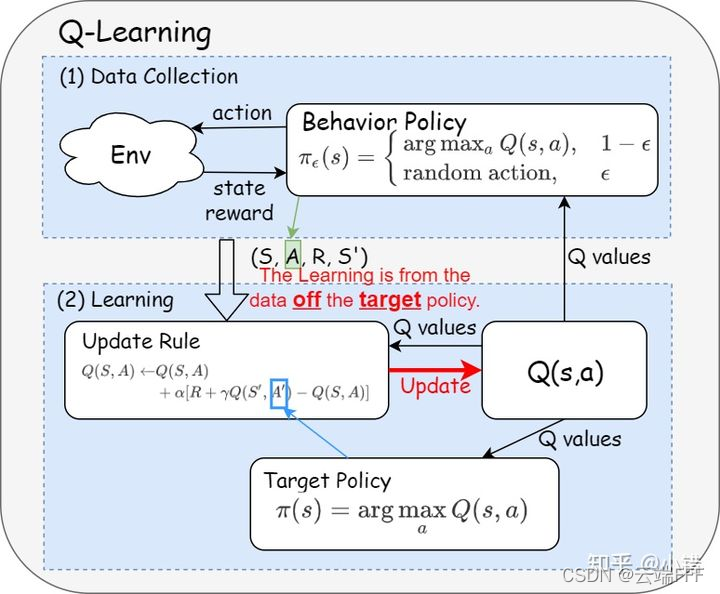
• 为了高效地进行探索，行为策略通常还是需要借助估计价值的指导，on-policy 中的不稳定（循环依赖）、数据相关性强、数据利用率低等几个问题仍然存在。但好消息是，off-policy 框架非常灵活，我们可以使用各种手段收集 transition 数据，如果能找到一个 “聪明的” 行为策略，总是能为算法提供最合适的样本，那么算法的效率将会得到提升

• 一个自然的想法是，我们可以把过去的经验 transition 保存下来重用，这样就能一举缓解上述三个问题，这个保存过去 transition 的机制就是 replay buffer，交互流程图示如下
  

• DQN 论文 Playing Atari with Deep Reinforcement Learning 首次将深度学习和 Q-learning 结合，并加入了 replay buffer 机制。其伪代码如下所示，蓝色部分把采样 transition 加入 replay buffer，黄色部分从 replay buffer 中均匀采样并更新价值价值网络参数
  

• 经验重放可以用更多的计算和内存来减少学习所需的样本数量，这通常比 agent 与环境的交互的成本低

2. 本文方法

2.1 思想：多重放高 TD error 的 transition

• 如 1.2 节伪代码所示，原始的 replay buffer 是随机均匀采样来更新的，但事实上，不同 transition 的重要性是不同的，如果更频繁地重放重要的 transition，那么就能进一步提升学习效率。为了验证这个想法，作者进行了一个简单的实验，如下所示
  

  1. 实验 MDP 如左图所示，这是一个稀疏奖励任务，agent 必须连续向右走 $n$ 步才能得到奖励（一个随机的行动序列获得奖励的几率是 $2^{?n}$）。这种情况下，和 reward 最相关的 transition 样本（来自罕见的成功）隐藏在大量高度冗余的错误样本中（类似于两足机器人在发现如何行走之前反复摔倒）
  2. 作者将 replay buffer 结合到 Q-leaning 算法中，第一个 agent 均匀地进行经验重放，第二个 agent 利用一个 oracle 来确定 transition 的优先级（这个 oracle 有上帝视角，它在参数更新后给出各个 transition 减少全局损失的程度）。作者以随机顺序执行所有可行的 $2^n$ 个轨迹来填充 replay buffer
  3. 作者通过改变 $n$ 的大小得到一系列不同难度的任务，两个 agent 学习值函数所需 learning step 的中位数对比如右图所示，可见理想的优先级重放可以指数级地加速学习

• 优先级重放的核心是设计衡量每个 transition 重要性的标准

  1. 最理想的标准是 agent 可以从当前状态的转换中学习的量（预期学习进度，即上面实验中 oracle 给出的值），但是这个值无法直接测量
  2. 一个合理的替代标准是 transition 的 TD error $\delta$ 的大小，这表明 transition 有多 “令人惊讶” 或 “出乎意料”

     这尤其适用于增量在线 RL 算法，如 SARSA 或 Q-learning，因为它们已经计算出 TD error $\delta$ ，并按照其比例更新参数

• 作者进一步实验了使用 TD error 设计重放优先级的有效性，实验 MDP 及 replay buffer 设置和上面相同，使用 TD error 绝对值 $|\delta |$ 大小作为优先级，并贪心地选择 $|\delta |$ 最大的 transition 进行重放。对于未见 transition，在加入 replay buffer 时将其设为最高优先级，以保证所有 transition 都至少计算一次，实验结果如下所示
  
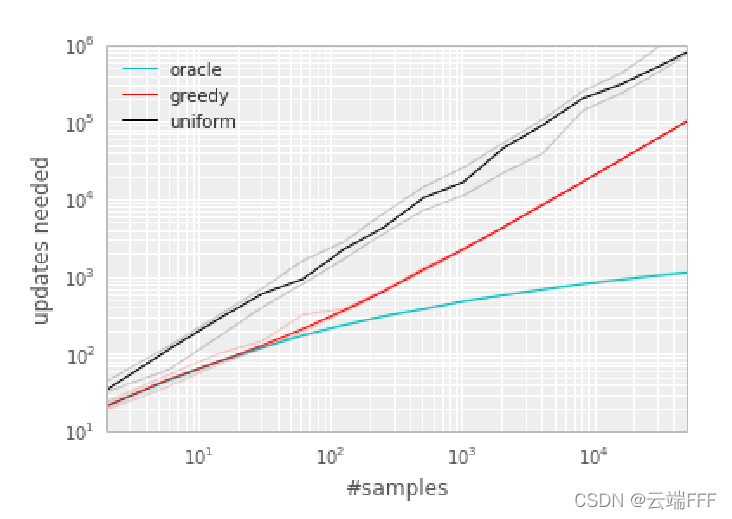
  可见，基于 TD error 设计重放优先级，虽然不如上帝 Oracle，但也带来了不小的性能提升

  注：作者在这个实验中对 Q 价值设置了乐观初始化。在使用 TD error 作为重放优先级时，随机（或乐观）初始化是必要的，因为若用零初始化，则无 reward 的 transition 最初 TD error $\delta =0$，因而其将被放置在队列的底部，直到其他 transition 上的 TD error 降至收敛阈值以下（都被调整完）后才有机会被重放

2.2 随机性排序

• 需要说明的是，在某些情况下，贪心地按照 TD error 进行重放可能是一个很差的选择，这是因为 TD error 只有在遇到对应的 $(s,a)$ transition 时才会更新，这导致几个后果

  1. 如果某个 transition 在第一次访问时 TD error 很小，则这个 transition 很难被采样到。当 replay buffer 使用滑动窗口更新时，甚至可能永远不会被采样到
  2. 对噪声尖峰很敏感，噪声可能来自随机性奖励或者函数估计误差，并会被 bootstrapping 机制加剧
  3. 降低 TD error 需要不少时间，这意味着贪心算法会频繁重放经验中高 TD error 的一小部分 transition，这种 diversity 的缺失会导致过拟合（这一条和第一条差不多）

• 为此，我们必须要在基于 TD error 的简单贪心重放策略中增加一些随机性，并且保证

  1. transition 的优先级 $p$ 应基于 TD error $\delta$ 进行设计，并且关于其绝对值 $|\delta |$ 是单调的
  2. transition 被采样的概率关于其优先级 $p$ 是单调的
  3. 即使是优先级最低的 transition，也要有一定的概率被重放

  具体地说，设第 $i$ 个样本优先级为 $p_i>0$，则其被采样的概率为
  $$P(i)=\frac{p_i^{\alpha }}{{\sum }_k{p}_k^{\alpha }}$$ 其中超参数 $\alpha$ 控制对优先级的倾向程度

  1. 当 $\alpha =0$ 时，退化为均匀采样
  2. 当 $\alpha >0$ 时，以 $\alpha$ 指数级倾向于优先级高的 transition

• 具体实现上，作者使用了一种叫做 “sum-tree” 的数据结构。这里可以用概率论中的几何概型去理解，如果把每个样本的 $p_i^{\alpha }$ 看成一段区间，那么所有样本可以拼成一个长 ${\sum }_k{p}_k^{\alpha }$ 的区间

  1. 要采样一个样本，只需在这个区间中随机选一个点并采样其所在区间对应的样本即可，因为该点落入第 $i$ 个样本对应区间的概率就是 $P(i)=\frac{p_i^{\alpha }}{{\sum }_k{p}_k^{\alpha }}$
  2. 对于常见的 mini-batch 情况，要采样 $k$ 个样本，可以先把区间均匀分割为 $k$ 段，然后在每一段中随机选一个点，取出 $k$ 个点落入区间对应的样本即可

  下图是 sum-tree 的采样示例（sum-tree 其实就是一个大顶堆，每个父节点大小是其两个子节点的和），详细说明可以参考 off-policy全系列（DDPG-TD3-SAC-SAC-auto）+优先经验回放PER-代码-实验结果分析
  

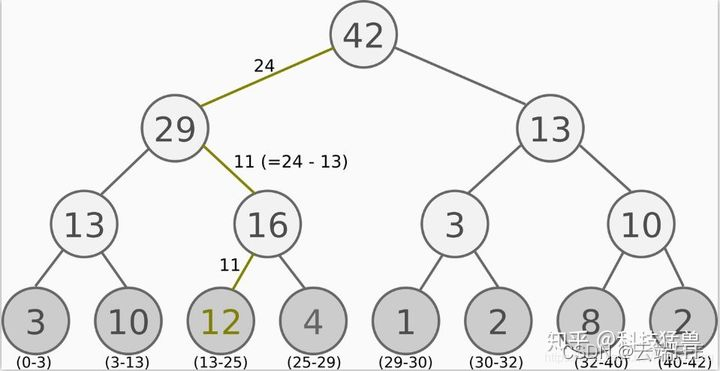
• 下面我们进一步考虑样本优先级 $p_i$ 的设计

2.2.1 优先级方案一：Proportional prioritization

• 第一个方案比较直接，根据 TD error 的大小比例直接设置优先级，具体来说设置为
  $$p_i=|{\delta }_i|+?$$ 这里 $?>0$ 是一个小正数，设置它是为了消除 $\delta =0$ 导致采样概率 $P(i)=0$ 的边界情况出现，这有点像拉普拉斯平滑

  注：如果对价值进行 0 初始化，那么 $\delta =0$ 的 transition 在训练早期特别常见，如果是稀疏奖励的情况就更常见了、

• 这种方案包含的信息量较多，可以反映出各个 transition TD error 的分布结构，但是鲁棒性较差，可能受到极端值影响

2.2.2 优先级方案二：Rank-based prioritization

• 第二个方案是间接的，根据 TD error 绝对值大小的排名来设计优先级，具体来说设置为
  $$p_i=\frac{1}{\text{rank(i)}}$$ 其中 $\text{rank(i)}$ 是 $|{\delta }_i|$ 的大小排名，这样我们得到的优先级服从幂律分布
  
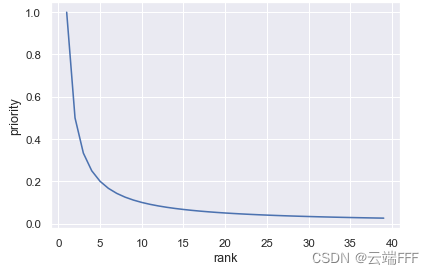
  由于幂律分布具有重尾特性，所以可以保证采样时的多样性
• 这种方案包含的信息量较少，无法反映各个 transition TD error 的分布结构，但是鲁棒性较强

2.3 消除偏差

• 非均匀采样会改变某个策略 $\pi$ 诱导的 $(s,a)$ 分布（或者说改变了策略的占用度量），这会导致学习价值网络时梯度方向出现偏差。如果你把经验重放看作行为策略的一部分可能更好理解一点，即使你的策略 $\pi$ 是固定的，使用不同的经验重放也会导致不同的行为策略，进而使得价值网络收敛到不同位置

2.3.1 产生偏差的原因

• 这里有一个比较有意思的事情，PER 是作为 DQN 系列方法的一个改进技巧被提出，而 DQN 是 Q-learning 和深度学习的结合，这一系列 off-policy 方法中，为何 Q-learning 和 DQN 都不需要考虑偏差呢? 要知道 off-policy 的 MC 方法是需要用重要性采样比去消除偏差的

  1. 对于 Q-learning 而言，其使用 Bellman optimal equation 作为更新公式，由于使用最优价值函数，其 Bellman 一致性条件可以用一种特殊的形式表示，不拘泥于任意特定的策略。从公式上看， Q-learning 的学习目标如下
     $$\begin{array}{rl}{Q}_{?}(s,a)& =\max {\mathbb{E}}_{{\pi }_{?}}[G_t|S_t=s,A_t=a]\\ & =\max {\mathbb{E}}_{{\pi }_{?}}[R_{t+1}+\gamma G_{t+1}|S_t=s,A_t=a]\\ & =\mathbb{E}[R_{t+1}+\gamma \underset{a^{\prime }}{\max }{Q}_{?}(S_{t+1},a^{\prime })|S_t=s,A_t=a]\\ & =\sum _{s^{\prime },r}p(s^{\prime },r|s,a)[r+\gamma \underset{a^{\prime }}{\max }{Q}_{?}(s^{\prime },a^{\prime })]\end{array}$$ 等式右侧的期望只与状态转移分布有关而与策略无关，不论训练 transition 来自于哪个策略，按照 Q-learning 的更新式更新都能使 $Q$ 函数接近 $Q^{?}$，又因为 Q-learning 是一个表格型方法，没有泛化性，对一个 $(s,a)$ 的价值更新完全不会影响到其他 $(s,a)$ 的价值估计，因而无论使用什么行为策略去收集 transition，都不会引入偏差，也就不需要重要性采样。不过，不同行为策略导致的价值收敛过程还是不一样的，行为策略更频繁访问 transition 的价值会更快收敛，当计算 transition 数量趋向无穷时，所有能无限采所有 $(s,a)$ 的行为策略最终会学到一样的价值函数 $Q$

     这就好像是用茶壶往一堆杯子里倒水，向一个杯子倒水不会干扰其他杯子。行为策略指导你向哪些杯子倒，其频繁访问的杯子更快装满水（价值收敛），如果所有杯子被访问的概率都大于 0，则时间趋于无穷时总能使所有杯子装满水（价值全部收敛到相同位置）

  2. 当引入神经网络估计价值时，由于其泛化性，情况有所不同了。对于 DQN 系列方法而言，其使用 $L_2$ 损失进行优化。如果做梯度下降的话，第 $i$ 轮迭代损失函数为
     $${\mathcal{L}}_i={\mathbb{E}}_{s,a～\rho (?)}[(y_i?Q(s,a,{\theta }_i{)}^2)]$$ 其中 $\rho$ 是行为策略诱导的 $(s,a)$ 分布，$y_i$ 是 TD target $$y_i={\mathbb{E}}_{s^{\prime }～\text{env}}[r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },{\theta }_{i?1})|s,a]$$ 损失函数梯度为
     $${▽}_{{\theta }_i}{\mathcal{L}}_i={\mathbb{E}}_{s,a～\rho (?),s^{\prime }～\text{env}}\left[\right(r+\gamma \underset{a^{\prime }}{\max }Q(s^{\prime },a^{\prime },{\theta }_{i?1})?Q(s,a,{\theta }_i)){▽}_{{\theta }_i}Q(s,a,{\theta }_i)]$$ 虽然这里依然是基于 Bellman optimal equation 来做更新，但是要注意到梯度期望中 $\rho$ 会受到行为策略影响。这本质上是由于神经网络的泛化性导致的，神经网络的梯度更新会影响到所有 $(s,a)$ 的价值，期望梯度方向来自 mini-batch 中的 transition 样本，这些样本的采集又受到行为策略影响，于是不同的行为策略就会导致价值网络收敛到不同位置

     这就好像是用水桶往一堆杯子泼水，往一个地方泼水，所有杯子都会溅到，水还可能洒出来。行为策略指导你向哪些泼水，这时行为策略的一点点区别，都会导致各个杯子最终的水量不同

     从这个角度分析，当 replay buffer 使用均匀采样时，对行为策略影响不大因，而不需要考虑偏差（replay transition 的分布是近期行为策略诱导 $(s,a)$ 分布的平均分布）

     事实上，DQN 的原始论文完全没有提到可能引入偏差这件事，我认为这里其实还是会有一点偏差的，因为 online RL 中行为策略在不断变化，replay buffer 中的 transition 毕竟还是来自比较老的策略
     ·

  3. 当向 DQN 系列方法中加入 RER 时，这时真正去更新价值网络的 $(s,a)$ 分布和行为策略诱导的 $(s,a)$ 分布会有很大区别了，加上神经网络泛化性的影响，价值估计偏差就会变得很大了（价值网络会过拟合到频繁采样重放的 transition 上），因此必须做重要性采样

2.3.2 消除偏差

• 为了使价值网络收敛到相同的结果，做重要性采样，使用系数 $w(i)$ 来调节第 $i$ 个 transition 样本的损失，即
  $${\mathcal{L}}_{\text{PER}}=w(i)\mathcal{L}(\delta (i))$$ 这里的系数使用重要性采样权重（importance sampling weights），具体为
  $$w_i=(\frac{1}{N}?\frac{1}{p(i)}{)}^{\beta }$$ 其中 $N$ 是 replay buffer 中的样本数，当 $\beta =1$ 时退化为均匀采样（还是会更多次重放高 TD error 的 transition，但这些 transition 的影响梯度的步长较小，期望梯度和均匀采样重放时相等）。在典型的强化学习场景中，由于策略、状态分布和引导目标的变化，梯度更新的无偏性在训练结束时接近收敛时最为重要，因为过程无论如何都是高度非平稳的，所以对 $\beta$ 进行退火处理，从 ${\beta }_0<1$ 线性增加到 $1$

  这里的重要性采样并不能完全消除 distribution shift，因为梯度下降的影响是类似积分那样的，早期 $\beta <1$ 时造成的影响仍会存在。可以在训练早期完成退火，然后在均匀重放的情况下继续训练较长时间，以缓解这种影响。另外作者也尝试了使 $\beta$ 恒等于 1 的情况，同样取得了性能提升

  最后，为了增加稳定性，通过除以最大值把 $w(i)$ 压缩到 $(0,1]$ 之间，即
  $$w(i)=\frac{w_i}{{\max }_j{w}_j}$$

• 作者文中还提出这样处理的另一个优点，TD error $|\delta (i)|$ 高的 transition，其损失梯度也比较大，通过重要性采样权重可以减小更新梯度，这有点相当于自适应地调整学习率，使算法能更好地跟踪高度非线性的函数曲线

2.4 伪代码

• 作者把 PER 和 DDQN 相结合，伪代码如下
  
• 一个要注意的点是，对于初次见到的 transition，在加入 replay buffer 时要将其优先级设为最大，以保证至少被采样一次

3. 实验

• 作者在 49 款 Atari 游戏环境上和使用均匀采样重放的 DQN 及 DDQN 进行了对比实验，模型设置上 PER DDQN 和均匀 DDQN 完全一致，只是采样方式改变了，另外由于 PER 更多地选择高 $|\delta |$ transition，步长 $\eta$ 减小了四倍
• 超参数选择上，作者进行了简单的网格搜索，结果如下
  1. Rank-based prioritization：$\alpha =0.7,\beta =0.5$
  2. Proportional prioritization：$\alpha =0.6,\beta =0.4$
• 实验过程中，作者从人类轨迹中采样轨迹起点（as introduced in Nair et al., 2015 and used in van Hasselt et al., 2016），这种方式要求 agent 具有更强的鲁棒性和泛化能力，因为其不能依赖于重复某个记住的轨迹

3.1 性能对比

• 49 款游戏平均性能提升
  
  
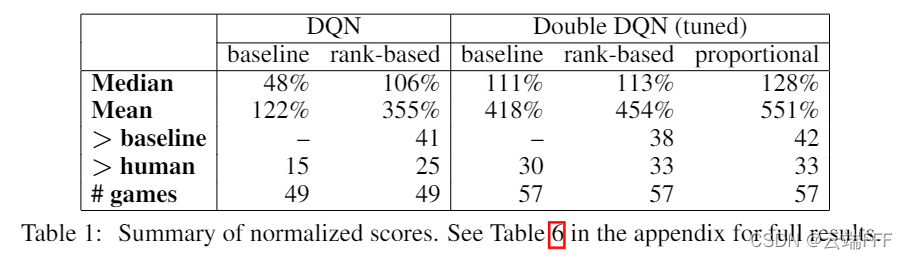
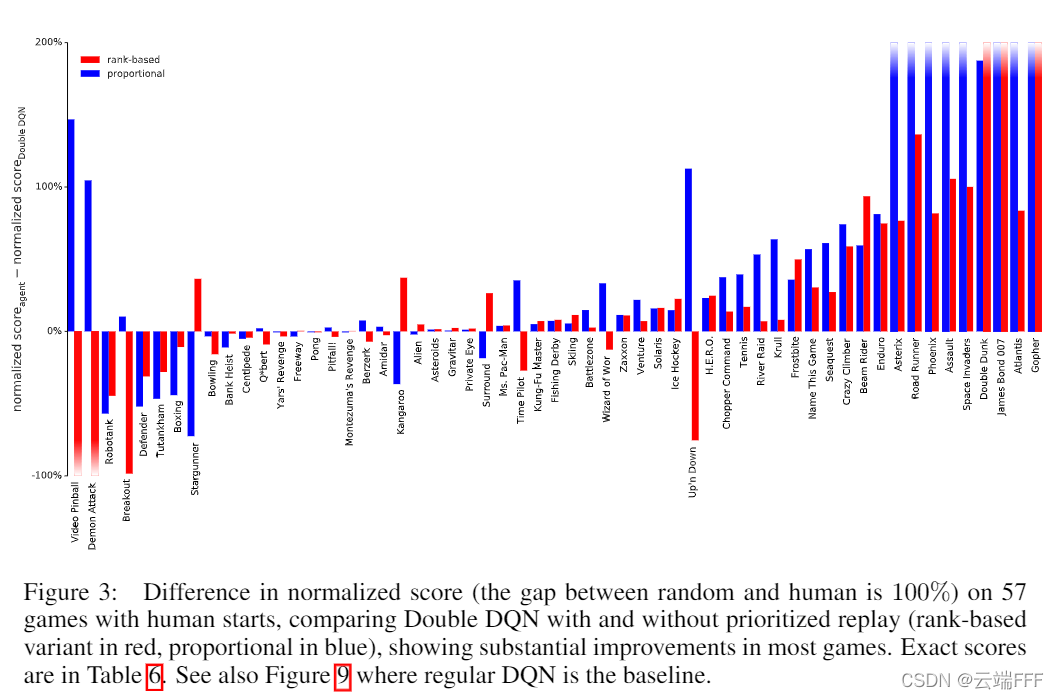
• 49 场游戏中有 41 场的性能得到提升（只要有一种优先级设置能提升性能就算）。可以观察到
  1. 虽然两种优先级排序的变体通常会产生类似的结果，但在有些游戏中，其中一种仍然接近 DDQN Baseline，而另一种会带来很大的提升
  2. PER 带来的性能提升和 DDQN 带来的性能提升是互补的

3.2 学习速度对比

• 通过学习曲线来观察学习速度
  
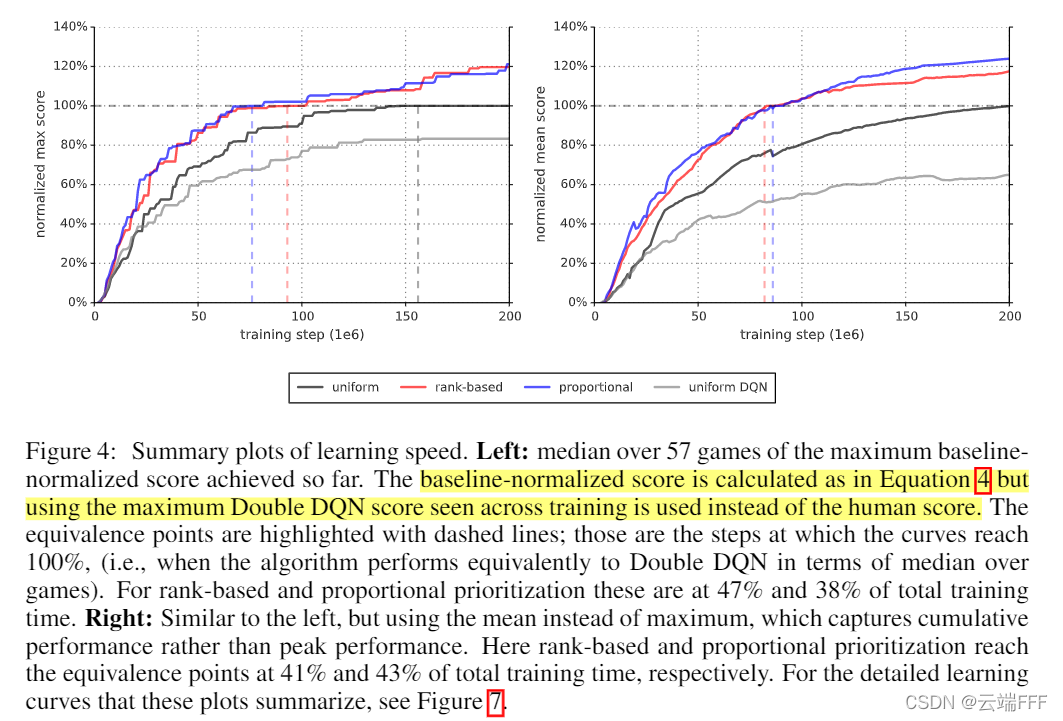
  作者发现使用 PER 可以将平均学习速度提升两倍，进一步观察不同游戏的学习曲线，作者与均匀采样重放的 Baseline 相比，在 Battlezone, Zaxxon 或 Frostbite 等受到延迟影响的游戏中，优先级重放可以有效地缩短性能提升前的盲目时间

3.3 完全修正偏差

• 在 2.3.2 节我们分析了，作者对超参数 $\beta$ 设置的退火策略会在价值网络的期望梯度方向中引入偏差，作者测试了如果设定 $\beta$ 恒等于 1（即完全修正偏差）的效果
  
• 这个测试中，完全修正 PER 和 Baseline 的步长 $\eta$ 相同，不完全修正 PER 的步长为其 $\frac{1}{4}$。作者发现
  1. 与不完全修正 PER 相比，完全修正 PER 使学习不那么积极，一方面导致初始学习较慢，但另一方面导致过早收敛的风险较小，有时最终结果更好
  2. 与均匀重放相比，完全修正 PER 平均性能更好

4. 讨论

• 对于两种优先级方案，作者猜想

  1. rank-based 方法会更稳健，因为它不受异常值或误差大小的影响，重尾特性保证了样本的多样性，并且来自不同误差分区的分层采样，会在整个训练过程中保持总的 mini-batch 梯度比较稳定
  2. 另一方面，rank-based 方法忽视了相对 TD error 的尺度，当要利用的 TD error 的分布结构时，这可能会导致性能下降，例如稀疏奖励场景

  实验发现两种变体在实践中表现相似，作者怀疑这是因为在 DQN 算法中大量使用了 clipping 操作（将 reward 和 TD error 裁剪到一个小区间中），这会去除异常值，避免 Proportional prioritization 方案受到太大影响

• 作者观察了 TD error 分布随时间的变化情况，如下
  
  这里线的颜色表示了其对应的时间（蓝色是开始时刻，红色是结束时刻），作者发现无论均匀采样重放还是 PER，都会使 TD error 分布接近重尾形式，但是 PER 会加速这个过程，这从经验上验证了 PER 公式 $P(i)=\frac{p_i^{\alpha }}{{\sum }_k{p}_k^{\alpha }}$ 的形式

• 作者还进一步分析的均匀采样重放和 PER 的区别

  1. 均匀采样重放的 transition 在加入 replay buffer 时没有给予其额外的优先度，这导致重放的很多经验都是过时的，甚至有些 transition 从而被重放过，PER 则纠正了这一点
  2. 作者把深度神经网络的顶层（学习 transition 的表示）与底层（改善价值估计）区分开来，表示良好的 transition 将迅速减少 TD error，然后被重放的次数减少，从而增加对表示较差的其他 transition 的学习

• 另外作者还进行了一些拓展探索，请参考原文