[人工智能]相机模型、标定与图像点云重建

1.单目相机模型

相机将三维世界中的坐标点（单位为米）映射到二维图像平面（单位为像素）的过程
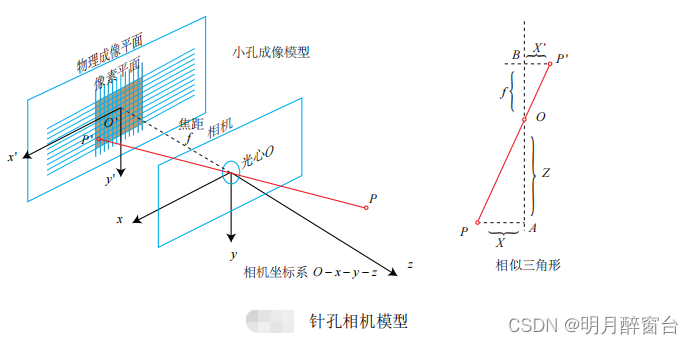
能够用一个几何模型进行描述。这个模型有很多种，其中最简单的称为针孔模型。针孔模
型是很常用，而且有效的模型，它描述了一束光线通过针孔之后，在针孔背面投影成像的
关系。在本书中我们用一个简单的针孔相机模型来对这种映射关系进行建模。同时，由于
相机镜头上的透镜的存在，会使得光线投影到成像平面的过程中会产生畸变。因此，我们
使用针孔和畸变两个模型来描述整个投影过程。
在本节我们先给出相机的针孔模型，再对透镜的畸变模型进行讲解。这两个模型能够
把外部的三维点投影到相机内部成像平面，构成了相机的内参数。

1.1 针孔相机模型

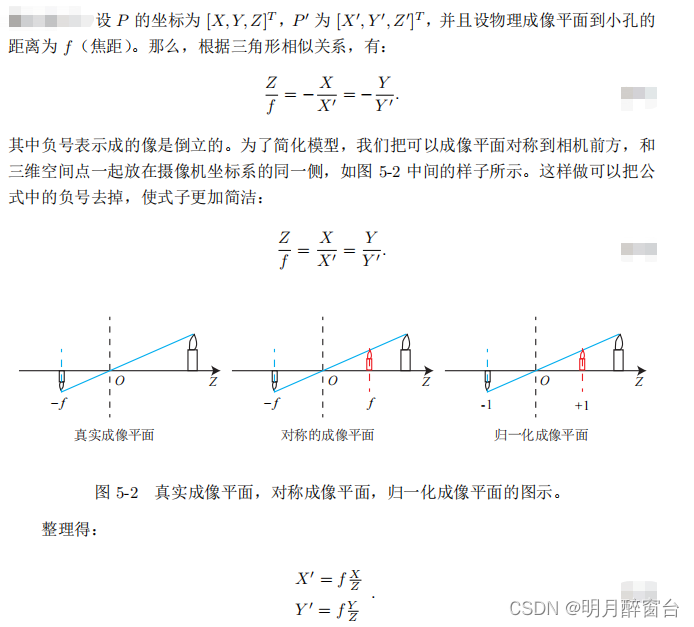
除了内参之外，自然还有相对的外参。考虑到我们使用的是 P 在相机坐标系下的坐标。由于相机在运动，所以 P 的相机坐标应该是它的世界坐标（记为 Pw），根据相机的当前位姿，变换到相机坐标系下的结果。相机的位姿由它的旋转矩阵 R 和平移向量 t 来描述。那么有

1.2 畸变

为了获得好的成像效果，我们在相机的前方加了透镜。透镜的加入对成像过程中光线的传播会产生新的影响: 一是透镜自身的形状对光线传播的影响，二是在机械组装过程中，透镜和成像平面不可能完全平行，这也会使得光线穿过透镜投影到成像面时的位置发生变化。
由透镜形状引起的畸变称之为径向畸变。在针孔模型中，一条直线投影到像素平面上
还是一条直线。可是，在实际拍摄的照片中，摄像机的透镜往往使得真实环境中的一条直线在图片中变成了曲线。越靠近图像的边缘，这种现象越明显。由于实际加工制作的透镜往往是中心对称的，这使得不规则的畸变通常径向对称。它们主要分为两大类，桶形畸变和枕形畸变，如图所示

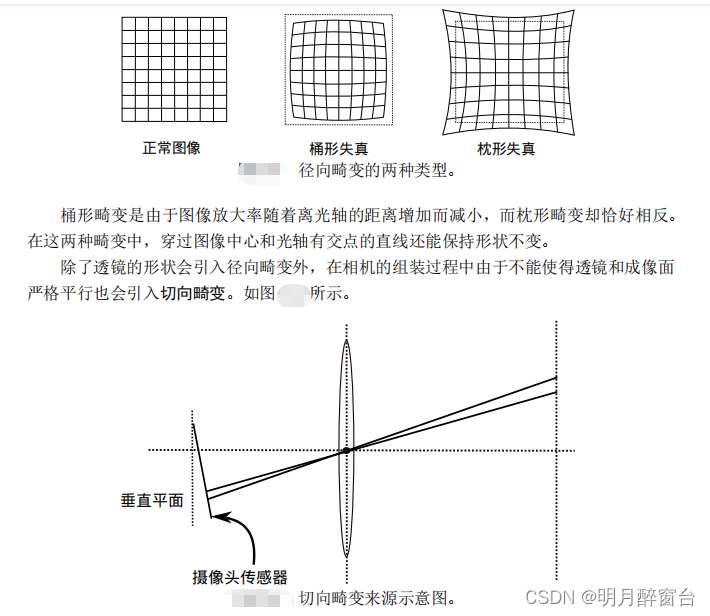
为更好地理解径向畸变和切向畸变，我们用更严格的数学形式对两者进行描述。我们知道平面上的任意一点 p 可以用笛卡尔坐标表示为 [x, y]T , 也可以把它写成极坐标的形式[r, θ]T，其中 r 表示点 p 离坐标系原点的距离，θ 表示和水平轴的夹角。径向畸变可看成坐标点沿着长度方向发生了变化 δr, 也就是其距离原点的长度发生了变化。切向畸变可以看成坐标点沿着切线方向发生了变化，也就是水平夹角发生了变化 δθ。


在上面的纠正畸变的过程中，我们使用了五个畸变项。实际应用中，可以灵活选择纠正模型，比如只选择 k1, p1, p2 这三项等。

2.双目相机模型

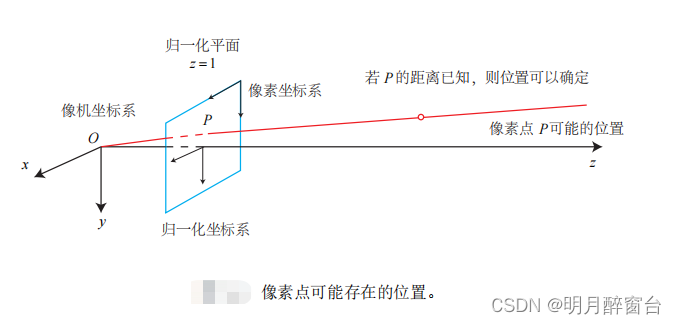
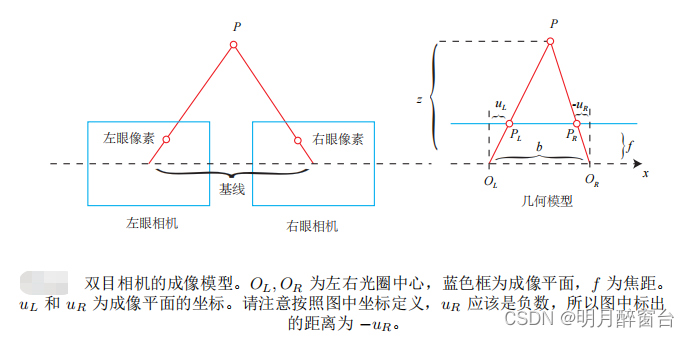
3. RGB-D相机模型

相比于双目相机通过视差计算深度的方式，RGB-D 相机的做法更为“主动”一些，它能够主动测量每个像素的深度。目前的 RGB-D 相机按原理可分为两大类：

1. 通过红外结构光（Structured Light）来测量像素距离的。例子有 Kinect 1 代、Project
   Tango 1 代、Intel RealSense 等；
   
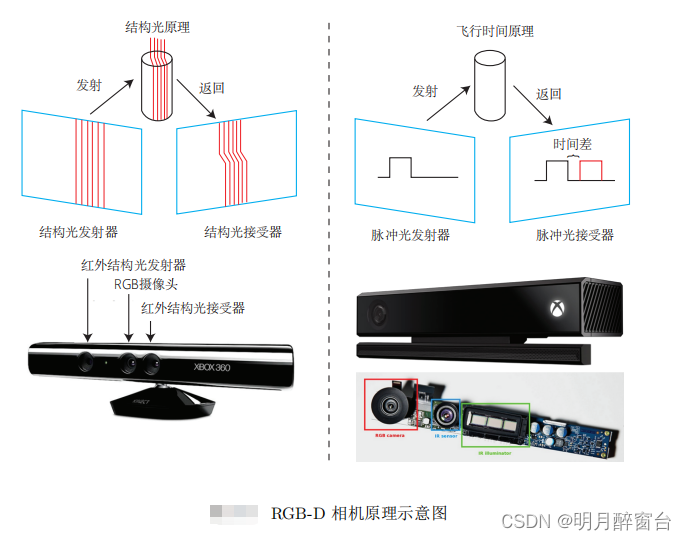
2. 通过飞行时间法（Time-of-flight, ToF）原理测量像素距离的。例子有 Kinect 2 代和一些现有的 ToF 传感器等。

4. 图像

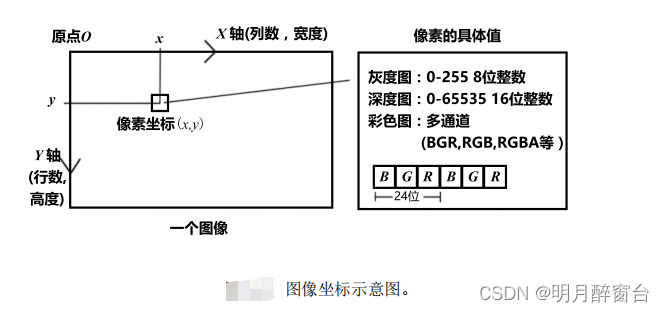
5. 实例：去畸变+3D点云重建
去畸变：

#include<opencv2/opencv.hpp>
#include<string>

using namespace std;
using namespace cv;

string img_file = "./ distorted.png";

int main()
{
	//也可用opencv的去畸变函数
	//畸变参数
	double k1 = -0.28340811, k2 = 0.07, p1 = 0.00019359, p2 = 1.76187114e-05;
	//内参
	double fx = 458.654, fy = 457.296, cx = 367.215, cy = 248.375;

	Mat image = imread(img_file, 0);
	int rows = image.rows, cols = image.cols;
	Mat image_undistort = Mat(rows, cols, CV_8UC1);//去畸变以后的图

	//计算去畸变以后的图像内容
	for (int v = 0; v < rows; ++v)
	{
		for (int u = 0; u < cols; ++u)
		{
			//按照公式，计算点(u,v)对应到畸变图像中的坐标(u_distorted,v_distorted)
			double x = (u - cx) / fx, y = (v - cy) / fy;
			double r = sqrt(x * x + y * y);
			double x_distorted = x * (1 + k1 * r * r + k2 * r * r * r * r) + 2 * p1 * x * y + p2 * (r * r + 2 * x * x);
			double y_distorted = y * (1 + k1 * r * r + k2 * r * r * r * r) + p1 * (r * r + 2 * x * x) + 2 * p2 * x * y;
			double u_distorted = fx * x_distorted + cx;
			double v_distorted = fy * y_distorted + cy;

			//赋值（最邻近插值）
			if (u_distorted >= 0 && v_distorted >= 0 && u_distorted < cols && v_distorted < rows)
			{
				image_undistort.at<uchar>(v, u) = image.at<uchar>(int(v_distorted), int(u_distorted));
			}
			else {
				image_undistort.at<uchar>(v, u) = 0;
			}
		}

		//imshow
		imshow("distorted", image);
		imshow("undistorted", image_undistort);
		waitKey();
	}
}

画出点云重建

int main()
{
	//内参
	double fx = 718.856, fy = 718.856, cx = 607.1928, cy = 185.2157;
	//基线
	double b = 0.753;

	//读取图像
	Mat left = imread(left_file, 0);
	Mat right = imread(right_file, 0);
	Ptr<StereoSGBM>sgbm = StereoSGBM::create(0, 96, 9, 8 * 9 * 9, 32 * 9 * 9, 1, 63, 10, 100, 32);
	Mat disparty_sgbm, disparty; 
	sgbm->compute(left, right, disparty_sgbm);
	disparty_sgbm.convertTo(disparty, CV_32F, 1.0 / 16.0f);

	//生成点云
	vector<Vector4d, Eigen::aligned_allocator<Vector4d>>pointcloud;

	for (int v = 0; v < left.rows; ++v)
	{
		for (int u = 0; u < left.cols; ++u)
		{
			if (disparty.at<float>(v, u) <= 10 || disparty.at<float>(v, u) >= 96.0)
				continue;

			Vector4d point(0, 0, 0, left.at<uchar>(v, u) / 255.0);//前三维xyz，第4维颜色

			//根据双目模型计算point的位置
			double x = (u - cx) / fx;
			double y = (v - cy) / fy;
			double depth = fx * b / (disparty.at<float>(v, u));
			point[0] = x * depth;
			point[1] = y * depth;
			point[2] = depth;

			pointcloud.push_back(point);

			imshow("disparty", disparty / 96.0);
			waitKey();

			//画出点云
			showPointCloud(pointcloud);
			return 0;
		}
	}
}

其他参考：
0.相机模型：单目、双目、深度相机模型及相机畸变

1.机器人手眼标定 https://zhuanlan.zhihu.com/p/76578691

2.使用最小二乘法+SVD分解 求空间点集的变换矩阵–数学原理

3.Ax=0超定方程的最小二乘解（基于OpenCV、基于Eigen的SVD分解）

4.RANSAC、最小二乘法、DLT