文章目录
1. Harris角点检测算法
1.1 什么是角点
角点(corner points):
? 局部窗口沿各方向移动,均产生明显变化的点
? 图像局部曲率突变的点
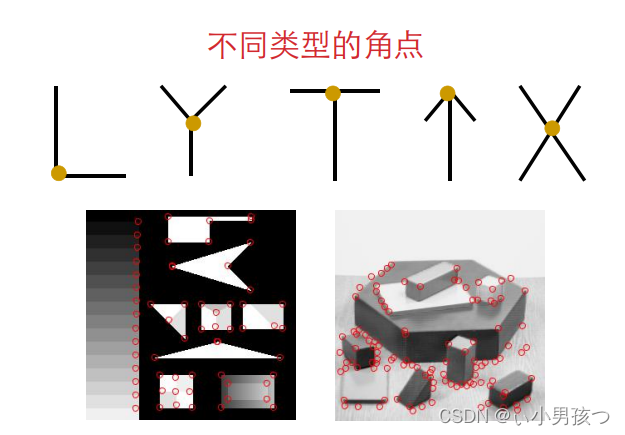
1.2 什么是好的角点检测算法
? 检测出图像中“真实的”角点
? 准确的定位性能
? 很高的稳定性
? 具有对噪声的鲁棒性
? 具有较高的计算效率
1.3 Harris角点检测算法基本思想
? 从图像局部的小窗口观察图像特征
? 角点定义 : 窗口向任意方向的移动都导致图像灰度的明显变化
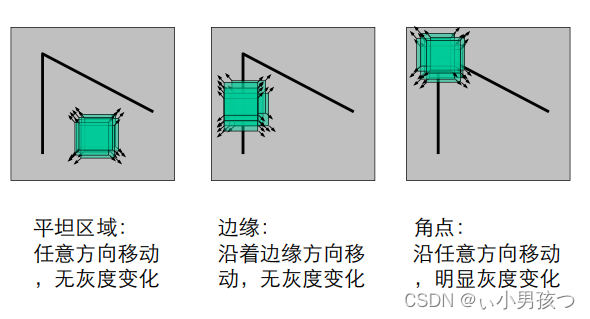
1.4 Harris检测的数学表达
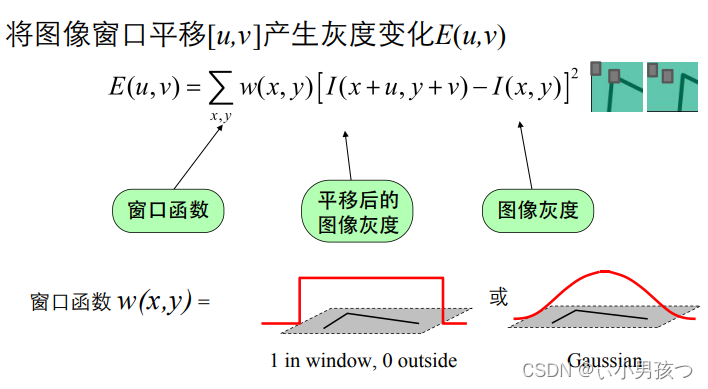
窗口移动导致的图像变化量:实对称矩阵M的特征值分析 
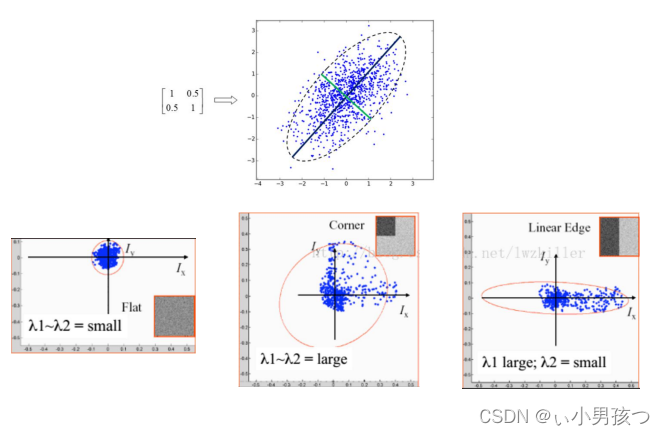
1.5 定义角点响应函数
我们定义角点响应函数R:
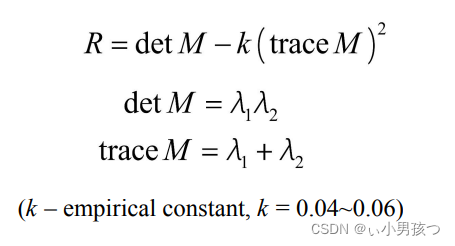
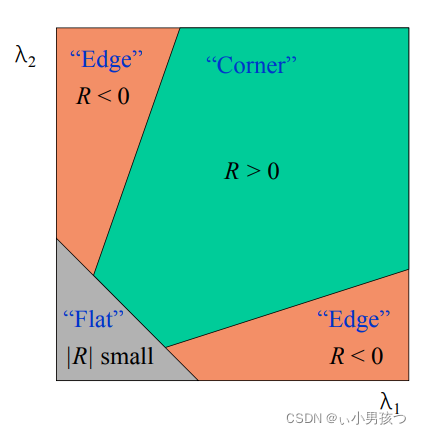
Harris矩阵Mi的特征值有三种情况:
1)如果 λ1和 λ 2都是很大的正数,则该x点为角点;
2)如果λ1很大,λ 2 很小(接近于0),则该区域内存在一个边,该区域内的平均Mi的特征值不会变化太大;
3)如果λ1λ2 都是很小的数 (λ1≈λ2≈0), 则该区域为空。
1.6 Harris角点检测实例
代码:
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris
# 读入图像
im = array(Image.open('JMU/6.jpg').convert('L'))
# 检测harris角点
harrisim = harris.compute_harris_response(im)
# Harris响应函数
harrisim1 = 255 - harrisim
figure()
gray()
#画出Harris响应图
subplot(141)
imshow(harrisim1)
print (harrisim1.shape)
axis('off')
axis('equal')
threshold = [0.01,0.1,0.2]
for i, thres in enumerate(threshold):
filtered_coords = harris.get_harris_points(harrisim, 6, thres)
subplot(1, 4, i+2)
imshow(im)
print(im.shape)
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
axis('off')
show()

1)为 Harris 响应函数;(2-4)分别为使用阈值 0.01、0.1 和 0.2 检测出的角点
结果分析:增大α的值,将减小角点响应值R,降低角点检测的灵性,减少被检测角点的数量;减小α值,将增大角点响应值R,增加角点检测的灵敏性,增加被检测角点的数量。使用阈值 0.01、01 和 0.2 检测出的角点依次减少。
1.7 寻找对应的点
Harris 角点检测器仅仅能够检测出图像中的兴趣点,但是没有给出通过比较图像间的兴趣点来寻找匹配角点的方法。我们需要在每个点上加入描述子信息,并给出一 个比较这些描述子的方法。
代码
from pylab import *
from PIL import Image
from PCV.localdescriptors import harris
from PCV.tools.imtools import imresize
im1 = array(Image.open("../JMU/15.jpg").convert("L"))
im2 = array(Image.open("../JMU/4.jpg").convert("L"))
# resize加快匹配速度
im1 = imresize(im1, (im1.shape[1]//2, im1.shape[0]//2))
im2 = imresize(im2, (im2.shape[1]//2, im2.shape[0]//2))
wid = 5
harrisim = harris.compute_harris_response(im1, 5)
filtered_coords1 = harris.get_harris_points(harrisim, wid+1)
d1 = harris.get_descriptors(im1, filtered_coords1, wid)
harrisim = harris.compute_harris_response(im2, 5)
filtered_coords2 = harris.get_harris_points(harrisim, wid+1)
d2 = harris.get_descriptors(im2, filtered_coords2, wid)
print('starting matching')
matches = harris.match_twosided(d1, d2)
figure()
gray()
harris.plot_matches(im1, im2, filtered_coords1, filtered_coords2, matches)
show()
效果展示

分析:虽然大部分得到了对应点的匹配,但是我们很明显也能看出该算法的结果中也存在一些不正确的匹配,这是因为,与现代的一些方法相比,图像像素块的互相关矩阵具有较弱的描述性。实际运用中,我们通常使用更稳健的方法来处理这些对应匹配。这些描述符还有一个问题,它们不具有尺度不变性和旋转不变性,而算法中像素块的大小也会影响对应匹配的结果。而且,Harris的算法效率也不高。
2. SIFT算法(尺度不变特征变换)
2.1 SIFT的目的和意义
1999年David G.Lowe教授总结了基于特征不变技术的检测方法,在图像尺度空间基础上,提出了对图像缩放、旋转保持不变性的图像局部特征描述算子-SIFT(尺度不变特征变换)。
2.2 SIFT算法可以解决的问题
? 目标的旋转、缩放、平移(RST)
? 图像仿射/投影变换(视点viewpoint)
? 弱光照影响(illumination)
? 部分目标遮挡(occlusion)
? 杂物场景(clutter)
? 噪声
2.3 SIFT算法步骤
- 提取关键点:比如角点、边缘点、暗区域的亮点以及亮区域的暗点
- 对关键点附加详细的信息(局部特征),即描述符;
- 通过特征点(附带上特征向量的关键点)的两两比较找出相互匹配的若干对特征点,建立景物间的对应关系。
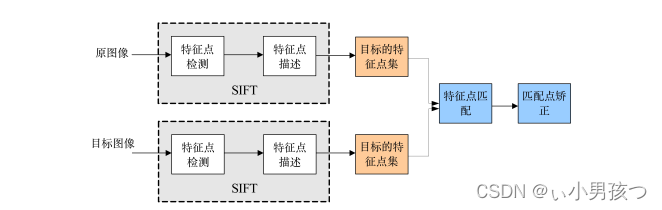
2.4 使用SIFT算法提取图像SIFT特征
代码:
from PIL import Image
from pylab import *
from PCV.localdescriptors import sift
from PCV.localdescriptors import harris
# 添加中文字体支持2
from matplotlib.font_manager import FontProperties
font = FontProperties(fname=r"d:\JsVison\font\SimSun.ttc", size=14)
imname = '../JMU/6.jpg'
im = array(Image.open(imname).convert('L'))
sift.process_image(imname, 'empire.sift')
l1, d1 = sift.read_features_from_file('empire.sift')
figure()
gray()
subplot(131)
sift.plot_features(im, l1, circle=False)
title(u'SIFT特征',fontproperties=font)
subplot(132)
sift.plot_features(im, l1, circle=True)
title(u'用圆圈表示SIFT特征尺度',fontproperties=font)
# 检测harris角点
harrisim = harris.compute_harris_response(im)
subplot(133)
filtered_coords = harris.get_harris_points(harrisim, 6, 0.1)
imshow(im)
plot([p[1] for p in filtered_coords], [p[0] for p in filtered_coords], '*')
axis('off')
title(u'Harris角点',fontproperties=font)
show()

2.5总结分析
SIFT算法的实质是在不同的尺度空间上查找关键点(特征点),并计算出关键点的方向。SIFT所查找到的关键点是一些十分突出,不会因光照,仿射变换和噪音等因素而变化的点,如角点、边缘点、暗区的亮点及亮区的暗点等。