论文?Efficient Channel Attention for Deep Convolutional Neural Networks
前言
SENet首先通过global average pooling对每个通道的空间信息进行编码,然后接两个FC层学习通道间的依赖关系,最后接sigmoid激活函数,每个通道输出一个0-1之间的权重,再与输入相乘得到最终结果,这种通道注意力机制可以让模型通过学习的权重去增强更有用通道的信息,抑制没那么重要的通道信息。为了减少参数和计算量,第一个FC将通道数映射为原来的 \(\frac{1}{r}\),这里的? \(r\) 是缩放比例,第二个FC再映射回去。
本文通过实验指出,降维对通道注意机制带来了副作用,破坏了通道与其权重之间的对应关系。如下图所示
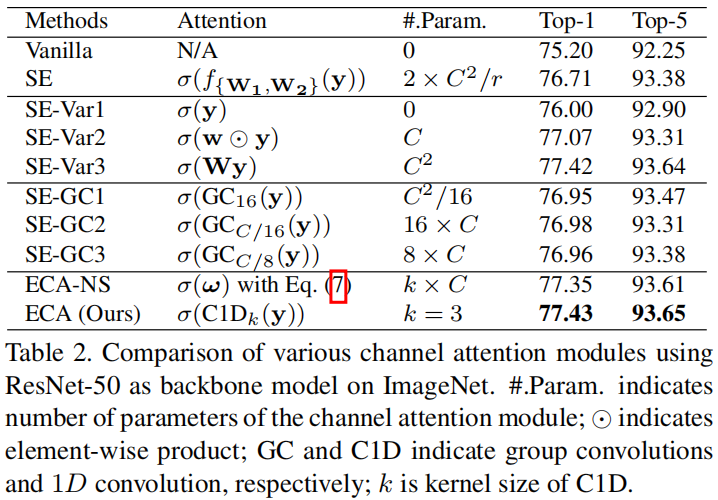
其中 \(y\) 是gap的输出,SE-Var1是直接接sigmoid,没有新学习的参数。SE-Var2是每个通道单独学一个权重,不考虑通道之间的关联,因此学习的参数就是通道数 \(C\) 。SE-Var3是接了一个FC,其中每个通道的权重都考虑到了所有通道的信息,FC是一个 \(C\times C\) 矩阵,因此学习的参数是 \(C^{2}\) 个。可以看出SE-Var2和SE-Var3都比原始的SE效果好,表明在通道注意力机制中,考虑通道间的关联带来的涨点还不如降维导致的掉点大。
介绍
因此作者在设计新的注意力机制时考虑的首先就是不降维,SE-Var2和SE-Var3学习的权重矩阵如下所示
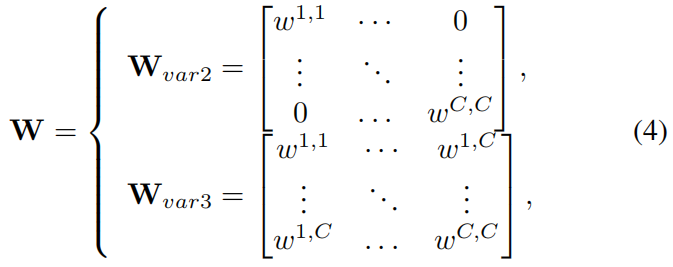
可以看出,他们都没有降维,但SE-Var2没有考虑通道间的关联而SE-Var3考虑到了,SE-Var3效果更好表明考虑通道间的关联是有用的,但是SE-Var3的参数又太多了。作者首先想的是按照group convolution的形式将通道分成 \(G\) 组,然后在每组内按SE-Var3的方式去学习,这样参数就降为 \(\frac{C^{2}}{G}\),权重矩阵如下所示
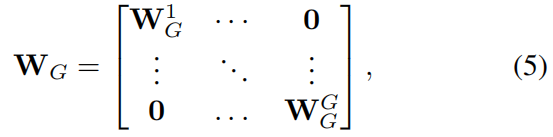
但是从表2的结果中可以看出 \(G\) 取不同值时的SE-GC的效果都不如SE-Var2,可能的原因是SE-GC完全没有考虑组之间的关联。因此作者提出如下所示的方法
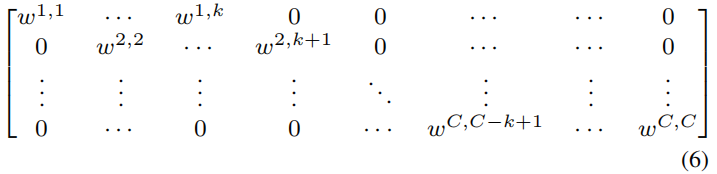
这样一共有 \(k\times C\) 个参数,同时这种方法也避免了式(5)中group之间的完全独立。更进一步,让所有通道共享相同的学习参数,参数进一步降为 \(k\) ,这样就可以通过一维卷积来实现,从表2可以看出,这种方法取得了最好的效果。
还有一个问题就是 \(k\) 怎么取,作者按是自适应地根据通道数 \(C\) 的不同选取不同的 \(k\) ,具体公式如下
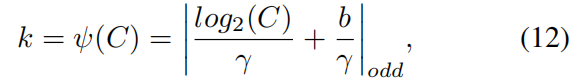
其中\(\gamma=2,b=1\),\(|t|_{odd}\)表示最接近 \(t\) 的奇数。例如当通道数\(C=1024\)时,\(k=|\frac{10+1}{2}|_{odd}=5\)
代码
from torch import nn
import math
def EfficientChannelAttention(x, gamma=2, b=1):
N, C, H, W = x.size()
t = int(abs(math.log(C, 2) + b) / gamma)
k_size = t if t % 2 else t + 1
avg_pool = nn.AdaptiveAvgPool2d(1)
conv = nn.Conv1d(1, 1, kernel_size=k_size, padding=(k_size - 1) // 2, bias=False)
sigmoid = nn.Sigmoid()
y = avg_pool(x)
y = conv(y.squeeze(-1).transpose(-1, -2)).transpose(-1, -2).unsqueeze(-1)
y = sigmoid(y)
return x * y.expand_as(x)