前言

迎浏览我的SLAM专栏，包括slam安装运行、代码注释、原理详解，一起加油淦穿SLAM。

一、地图点

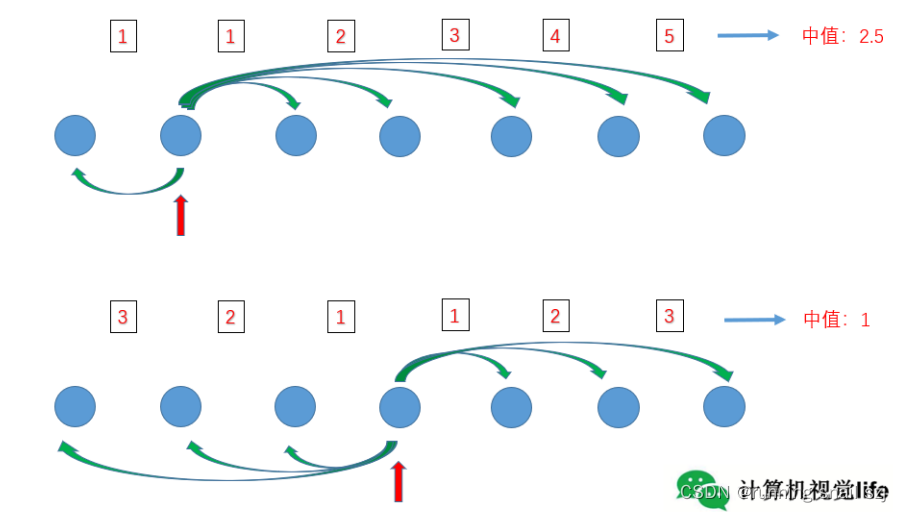
1.地图点代表性描述子的计算

找最有代表性的描述子示意图
最有代表的描述子与其他描述子具有最小的距离中值
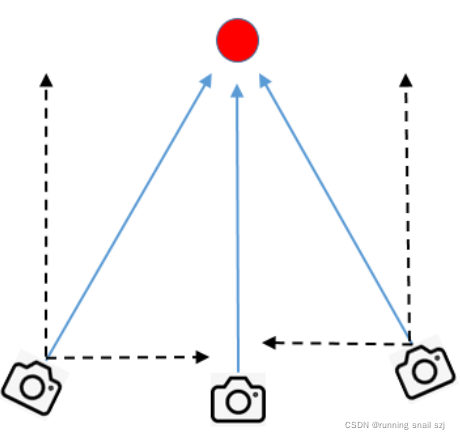
在这里插入图片描述
地图点法线朝向的计算

2.地图点和特征点的区别？

地图点是三维点，来自真实世界的三维物体，有唯一的id。不同帧里的特征点可能对应三维空间中同一个三维点，
特征点是二维点，是特征提取的点，大部分二维点在三维空间中没有对应地图点
生成地图点
关于生成地图点，主要有以下几个地方：

单目初始化时前两帧匹配生成地图点，双目左右目匹配生成地图点，RGB-D测量得到的地图点
local mapping里共视关键帧之间用 LocalMapping::CreateNewMapPoints() 生成地图点
Tracking::UpdateLastFrame() 和 Tracking::CreateNewKeyFrame()
中为双目和RGB-D生成了新的临时地图点，单目不生成

二、关键帧

1.什么是关键帧？

通俗来说，关键帧就是几帧普通帧里面具有代表性的一帧。

在这里插入图片描述
为什么需要关键帧

相近帧之间信息冗余度很高，关键帧是取局部相近帧中最有代表性的一帧，可以降低信息冗余度。举例来说，摄像头放在原处不动，普通帧还是要记录的，但关键帧不会增加。
关键帧选择时还会对图片质量、特征点质量等进行考察，在Bundle Fusion、RKD SLAM等RGB-D SLAM相关方案中常常用普通帧的深度投影到关键帧上进行深度图优化，一定程度上关键帧是普通帧滤波和优化的结果，防止无用的或错误的信息进入优化过程而破坏定位建图的准确性。
如果所有帧全部参与计算，不仅浪费了算力，对内存也是极大的考验，这一点在前端vo中表现不明显，但在后端优化里是一个大问题，所以关键帧主要作用是面向后端优化的算力与精度的折中，使得有限的计算资源能够用在刀刃上，保证系统的平稳运行。假如你放松 ORB_SLAM2关键帧选择条件，大量产生的关键帧不仅耗计算资源，还会导致local mapping 计算不过来，出现误差累积

2.如何选择关键帧？

选择关键帧主要从关键帧自身和关键帧与其他关键帧的关系2方面来考虑。

关键帧自身质量要好，例如不能是非常模糊的图像、特征点数量要充足、特征点分布要尽量均匀等等；
关键帧与其他关键帧之间的关系，需要和局部地图中的其他关键帧有一定的共视关系但又不能重复度太高，以达到既存在约束，又尽量
少的信息冗余的效果。

选取的指标主要有：

距离上一关键帧的帧数是否足够多（时间）——比如我每隔固定帧数选择一个关键帧，这样编程简单但效果不好。比如运动很慢的时候，就会选择大量相似的关键帧，冗余，运动快的时候又丢失了很多重要的帧。
距离最近关键帧的距离是否足够远（空间）/运动——比如相邻帧根据pose计算运动的相对大小，可以是位移也可以是旋转或者两个都考虑，运动足够大（超过一定阈值）就新建一个关键帧，这种方法比第一种好。但问题是如果对着同一个物体来回扫就会出现大量相似关键帧。
跟踪局部地图质量（共视特征点数目）——记录当前视角下跟踪的特征点数或者比例，当相机离开当前场景时（双目或比例明显降低）才会新建关键帧，避免了第2种方法的问题。缺点是数据结构和逻辑比较复杂。

在这里插入图片描述
在关键帧的运用上，我认为orbslam2做的非常好，跟踪线程选择关键帧标准较宽松，局部建图线程再跟据共视冗余度进行剔除，尤其是在回环检测中使用了以关键帧为代表的帧“簇”的概念，回环筛选中有一步将关键帧前后10帧为一组，计算组内总分，以最高分的组的0.75为阈值，滤除一些组，再在剩下的组内各自找最高分的一帧作为备选帧，这个方法非常好地诠释了“关键帧代表局部”的这个理念。

3.关键帧的类型及更新连接关系

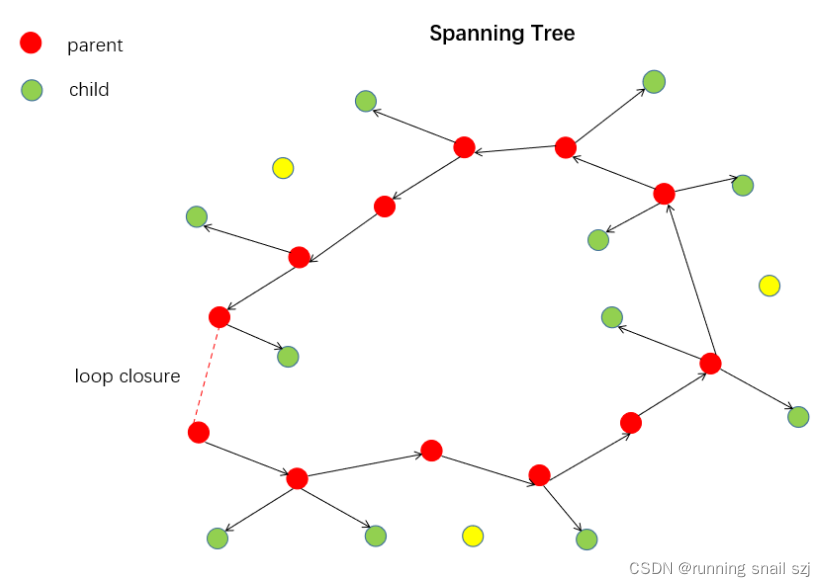
父子关键帧

//KeyFrame.h 文件中
bool mbFirstConnection; // 是否是第一次生成树
KeyFrame* mpParent; // 当前关键帧的父关键帧 （共视程度最高的）
std::set<KeyFrame*> mspChildrens; // 存储当前关键帧的子关键帧

更新连接关系

//KeyFrame.cc
KeyFrame::UpdateConnections()
{
//省略...
// Step 5 更新生成树的连接
if(mbFirstConnection && mnId!=0)
{
// 初始化该关键帧的父关键帧为共视程度最高的那个关键帧
mpParent = mvpOrderedConnectedKeyFrames.front();
// 建立双向连接关系，将当前关键帧作为其子关键帧
mpParent->AddChild(this);
mbFirstConnection = false;
}
}
// 添加子关键帧（即和子关键帧具有最大共视关系的关键帧就是当前关键帧）
void KeyFrame::AddChild(KeyFrame *pKF)
{
unique_lock<mutex> lockCon(mMutexConnections);
mspChildrens.insert(pKF);
}
// 删除某个子关键帧
void KeyFrame::EraseChild(KeyFrame *pKF)
{
unique_lock<mutex> lockCon(mMutexConnections);
mspChildrens.erase(pKF);
}
// 改变当前关键帧的父关键帧
void KeyFrame::ChangeParent(KeyFrame *pKF)
{
unique_lock<mutex> lockCon(mMutexConnections);
// 添加双向连接关系
mpParent = pKF;
pKF->AddChild(this);
}
//获取当前关键帧的子关键帧
set<KeyFrame*> KeyFrame::GetChilds()
{
unique_lock<mutex> lockCon(mMutexConnections);
return mspChildrens;
}
//获取当前关键帧的父关键帧
KeyFrame* KeyFrame::GetParent()
{
unique_lock<mutex> lockCon(mMutexConnections);
return mpParent;
}
// 判断某个关键帧是否是当前关键帧的子关键帧
bool KeyFrame::hasChild(KeyFrame *pKF)
{
unique_lock<mutex> lockCon(mMutexConnections);
return mspChildrens.count(pKF);
}

更新局部关键帧

void Tracking::UpdateLocalKeyFrames()
{
//省略...
// 策略2.2:将自己的子关键帧作为局部关键帧（将邻居的子孙们拉拢入伙）
const set<KeyFrame*> spChilds = pKF->GetChilds();
for(set<KeyFrame*>::const_iterator sit=spChilds.begin(), send=spChilds.end(); sit!=send; sit++)
{
KeyFrame* pChildKF = *sit;
if(!pChildKF->isBad())
{
if(pChildKF->mnTrackReferenceForFrame!=mCurrentFrame.mnId)
{
mvpLocalKeyFrames.push_back(pChildKF);
pChildKF->mnTrackReferenceForFrame=mCurrentFrame.mnId;
//? 找到一个就直接跳出for循环？
break;
}
}
}
// 策略2.3:自己的父关键帧（将邻居的父母们拉拢入伙）
KeyFrame* pParent = pKF->GetParent();
if(pParent)
{
// mnTrackReferenceForFrame防止重复添加局部关键帧
if(pParent->mnTrackReferenceForFrame!=mCurrentFrame.mnId)
{
mvpLocalKeyFrames.push_back(pParent);
pParent->mnTrackReferenceForFrame=mCurrentFrame.mnId;
//! 感觉是个bug！如果找到父关键帧会直接跳出整个循环
break;
}
}
// 省略....
}

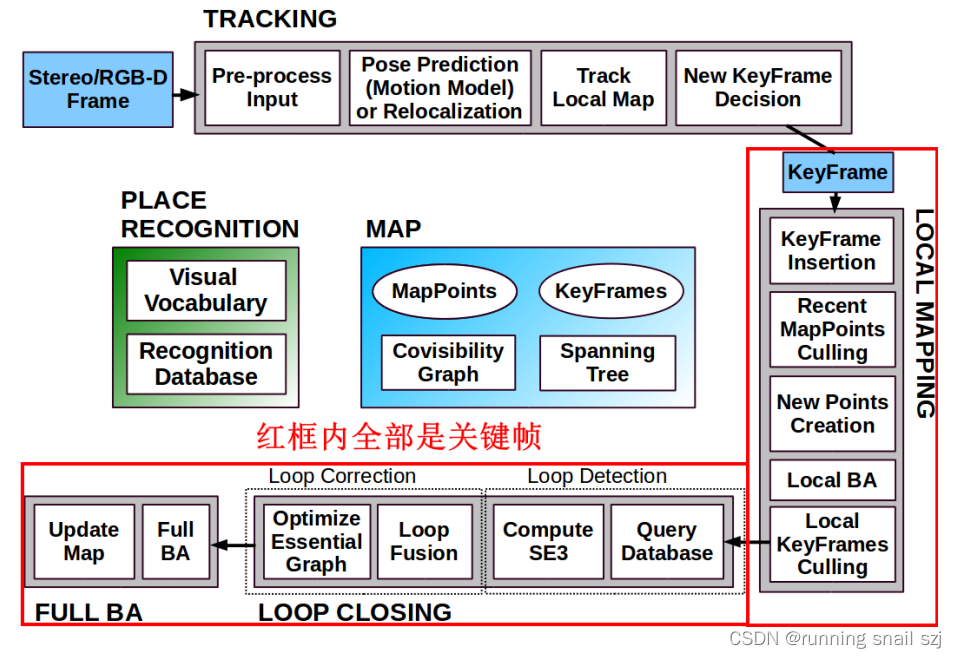
三、共视图本质图拓展树

在这里插入图片描述

1.共视图（Covisibility Graph）

共视图是无向加权图，每个节点是关键帧，如果两个关键帧之间满足一定的共视关系（至少15个共同观测地图点）他们就连成一条边，边的权重就是共视地图点数目
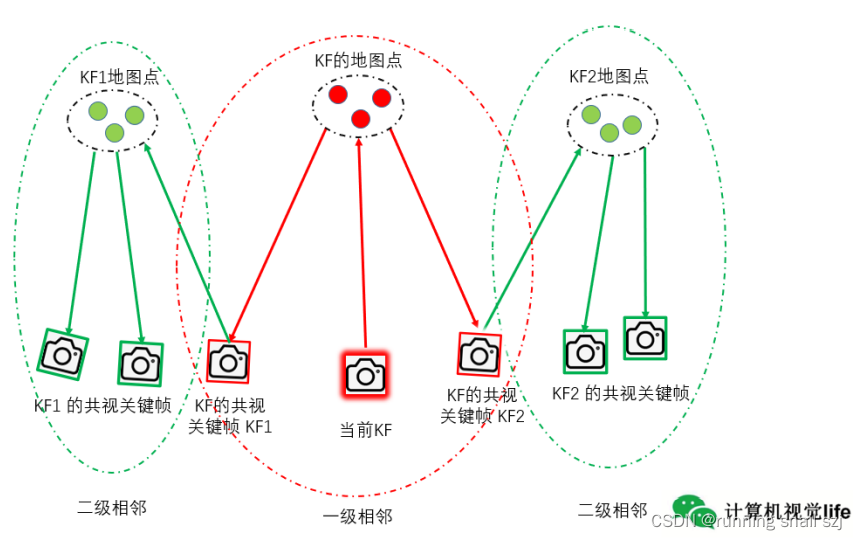
在这里插入图片描述
共视图的作用：

跟踪局部地图，扩大搜索范围
Tracking:UpdateLocalKeyFrames（）
局部建图里关键帧之间新建地图点 LocalMapping:：CreateNewMapPoints（）
LocalMapping:SearchlnNeighbors（）
闭环检测、重定位检测 LoopClosing:：DetectLoop（）、LoopClosing:CorrectLoop（）
KeyFrameDatabase:：DetectLoopCandidates
KeyFrameDatabase:：DetectRelocalizationCandidates
优化 Optimizer:：OptimizeEssentialGraph

2.本质图（Essential Graph）

共视图比较稠密，本质图比共视图更稀疏，这是因为本质图的作用是用在闭环矫正时，用相似变换来矫正尺度漂移，把闭环误差均摊在本质
图中。本质图中节点也是所有关键帧，但是连接边更少，只保留了联系紧密的边来使得结果更精确。本质图中包含：

生成树连接关系
形成闭环的连接关系，闭环后地图点变动后新增加的连接关系
共视关系非常好（至少100个共视地图点）的连接关系

本质图优化

//Optimizer.cc
Optimizer::OptimizeEssentialGraph()
{
// 省略....
// Spanning tree edge
// Step 4.1：添加生成树的边（有父关键帧）
// 父关键帧就是和当前帧共视程度最高的关键帧
if(pParentKF)
{
int nIDj = pParentKF->mnId;
g2o::Sim3 Sjw;
LoopClosing::KeyFrameAndPose::const_iterator itj = NonCorrectedSim3.find(pParentKF);
// 尽可能得到未经过Sim3传播调整的位姿
if(itj!=NonCorrectedSim3.end())
Sjw = itj->second;
else
Sjw = vScw[nIDj];
// 计算父子关键帧之间的相对位姿
g2o::Sim3 Sji = Sjw * Swi;
g2o::EdgeSim3* e = new g2o::EdgeSim3();
e->setVertex(1, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDj)));
e->setVertex(0, dynamic_cast<g2o::OptimizableGraph::Vertex*>(optimizer.vertex(nIDi)));
// 希望父子关键帧之间的位姿差最小
e->setMeasurement(Sji);
// 所有元素的贡献都一样;每个误差边对总误差的贡献也都相同
e->information() = matLambda;
optimizer.addEdge(e);
}
// 省略....
}

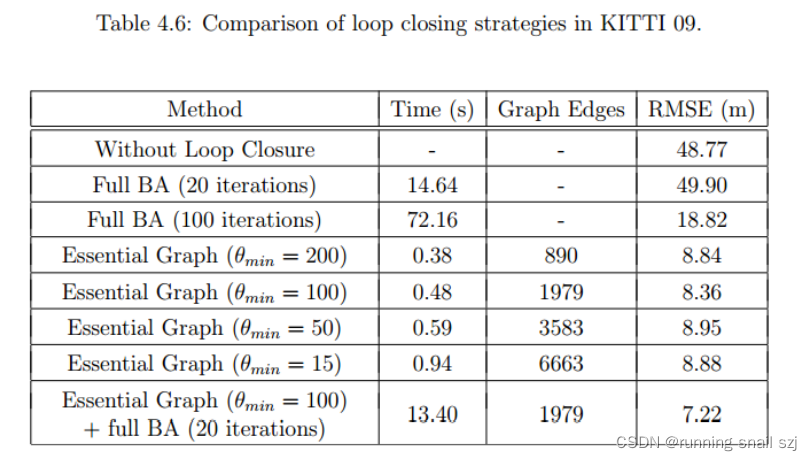
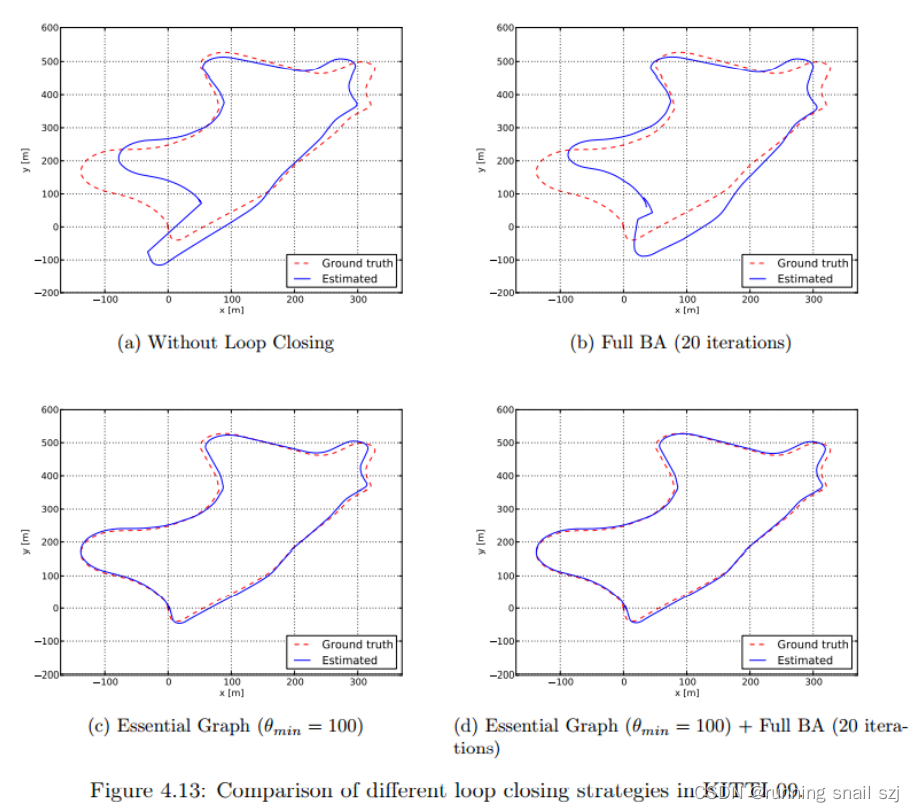
本质图优化和全局BA结果对比
从结果来看，

全局BA存在收敛问题。即使迭代100次，相对均方误差RMSE 也比较高
essential graph 优化可以快速收敛并且结果更精确。θmin 表示被选为essential
graph至少需要的共视地图点数目，从结果来看，θmin的大小对精度影响不大，但是较大的θmin值可以显著减少运行时间
essential graph 优化后增加全局 full BA 可以提升精度（但比较有限），但是会耗时较多

在这里插入图片描述