[人工智能]概率机器学习中的互信息（Mutual Information）

1.Mutual Information概念

互信息是信息论中用以评价两个随机变量之间的依赖程度的一个变量

2.信息论的基础概念

• 信息量： 是对某个时间发生的概率的度量，通常来讲一个事件发生的概率越低，则这个事件包含的信息量越大。在现实生活中，越稀奇的新闻（发生的概率小）包含的信息量越大。香农提出了一个定量衡量信息量的公式：
  $$log\frac{1}{p}=?logp$$

• 熵（entropy）： 衡量一个系统的稳定程度。其实就是一个系统所有变量信息量的期望或者均值。离散变量 公式为：
  $$H(X)=\sum _{x\in X}P(x)?log\frac{1}{P(x)}=?\sum _{x\in X}P(x)logP(x)=?ElogP(X)$$
  $P(x)$表示事件$X$为$x$发生的概率。如果一个系统越简单，出现情况种类很少（极端情况为1种情况，那么对应概率为1，那么对应的信息熵为0），此时的信息熵较小。连续变量，此时可以理解成它的概率密度函数，公式为：
  $$H(X)=\int P(x)?log\frac{1}{P(x)}dx$$

• 联合熵（joint entropy）： 多个联合变量的熵，也就是将熵的定义推广到多变量的范围。
  $$H(X,Y)=\sum _{x\in X}\sum _{y\in Y}P(x,y)?log\frac{1}{P(x,y)}=?\sum _{x\in X}\sum _{y\in Y}P(x,y)logP(x,y)=?ElogP(X，Y)$$

• 条件熵（conditional entropy）： 一个随机变量在给定的情况下，系统的熵。
  $$H(Y|X)=\sum _{x\in X}P(x)H(Y|X=x)=\sum _{x\in X}P(x)[\sum _{y\in Y}P(y|x)log\frac{1}{P(y|x)}]=\sum _{x\in X}\sum _{y\in Y}P(x)P(y|x)log\frac{1}{P(y|x)}=?ElogP（Y|X）$$

  条件熵就是假设在给定的一个变量下，该系统信息量的期望

• 相对熵（relative entropy）： 也被称作KL散度（Kullback-Leibler divergence）。当我们获得了一个变量的概率分布时，一般我们会找一种近似且简单的分布来代替。相对熵就是用来衡量两个分布对于同一个变量的差异情况。
  $$D_{KL}(p||q)=\sum _{i}p(x_i)?[log\frac{1}{q(x_i)}?log\frac{1}{p(x_i)}]=\sum _{i}p(x_i)?log\frac{p(x_i)}{q(x_i)}$$

• 交叉熵（cross entropy）： 也是用来衡量两个分布之间的差异性。
  $$H_{CE}(p，q)=\sum _{i}p(x_i)?log\frac{1}{q(x_i)}$$
  显然交叉熵是相对熵的第一部分，因为在通常情况下我们是已知?,即第二部分是常量，此时交叉熵和相对熵是一个线性关系，在考虑计算量的情况下，所以我们通常都用这部分交叉熵来做。

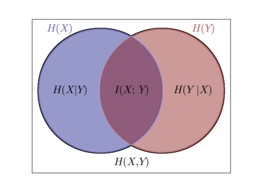
• 互信息（Mutual Information）： 如下图，互信息就是交叉的部分。根据熵的联锁规则，有：
  $$H(X|Y)=H(X)+H(Y|X)=H(Y)+H(X|Y)$$.因此，
  $$H(X)?H(X|Y)=H(Y)?H(Y|X)$$
  这个差叫做X和Y的互信息，记做$I(X|Y)$.按照熵的定义可以展开得到：
  $$I(X,Y)=H(X)?H(X|Y)=H(X)+H(Y)?H(X,Y)=\sum _{x}p(x)log\frac{1}{p(x)}+\sum _{y}p(y)log\frac{1}{p(y)}?\sum _{x,y}p(x,y)log\frac{p(x,y)}{p(x)p(y)}$$