异常值

在一般的预测问题中，模型通常是对整体样本数据结构的一种表达方式，这种表达方式通常抓住的是整体样本一般性的性质，而那些在这些性质上表现完全与整体样本不一致的点，我们就称其为异常点，通常异常点在预测问题中是不受开发者欢迎的，因为预测问题通产关注的是整体样本的性质，而异常点的生成机制与整体样本完全不一致，如果算法对异常点敏感，那么生成的模型并不能对整体样本有一个较好的表达，从而预测也会不准确。
从另一方面来说，异常点在某些场景下反而令分析者感到极大兴趣，如疾病预测，通常健康人的身体指标在某些维度上是相似，如果一个人的身体指标出现了异常，那么他的身体情况在某些方面肯定发生了改变，当然这种改变并不一定是由疾病引起（通常被称为噪音点），但异常的发生和检测是疾病预测一个重要起始点。相似的场景也可以应用到信用欺诈，网络攻击等等。

常见的异常值检测方法

简单统计
3σ原则
箱线图法

常见的异常值处理方法

删除
视为缺失值——用缺失值处理方法处理（填充，插值等）异常值

3σ原则

这个原则有个条件：数据需要服从正态分布。在3σ原则下，异常值如超过3倍标准差，那么可以将其视为异常值。正负3σ的概率是99.7%，那么距离平均值3σ之外的值出现的概率为P(|x-u| > 3σ) <= 0.003，属于极个别的小概率事件。
如果数据不服从正态分布，也可以用远离平均值的多少倍标准差来描述。

在这里插入图片描述

首先检验数据是否正态分布

# pvalue大于0.05则认为数据呈正态分布
from scipy import stats
mean = df['age'].mean()
std = df['age'].std()
print(stats.kstest(df['age'],'norm',(mean,std)))

异常值处理

# 选取小于3个标准差的数据
data = data[np.abs(df['age']- mean) <= 3*std]

如果数据不符合正态分布，也可以用远离平均值的多少倍标准差来筛选异常值。具体倍数看数据情况和业务需求

# 定义远离平均值4倍标准差为异常值
a = mean + std*4
b = mean - std*4
data = data[(data['Age'] <= a) & (data['Age'] >= b)]

箱线图

这种方法是利用箱型图的四分位距（IQR）对异常值进行检测，也叫Tukey‘s test。
四分位距(IQR)就是上四分位与下四分位的差值。而我们通过IQR的1.5倍为标准，规定：超过上四分位+1.5倍IQR距离，或者下四分位-1.5倍IQR距离的点为异常值。
在这里插入图片描述

画箱线图

data['Age'].plot(kind = 'box')

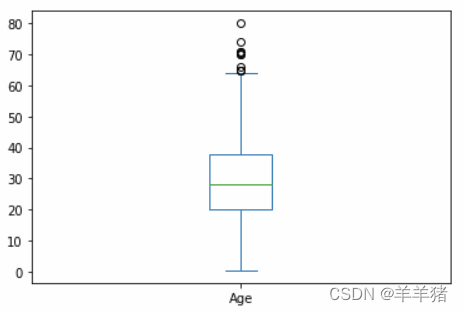
在这里插入图片描述

异常值处理

# 算出上界和下届
q1 = data["Age"].quantile(0.25)
q3 = data["Age"].quantile(0.75)
iqr = q3 - q1
bottom = q1 - 1.5*iqr
upper = q3 + 1.5*iqr

# 去除异常值
data[(data['Age'] >= bottom) & (data['Age'] <= upper)]