1-SVM简介
支持向量机(support vector machines, SVM):是一种二分类模型,它的基本模型是定义在特征空间上的间隔最大的线性分类器,间隔最大使它有别于感知机;SVM还包括核技巧,这使它成为实质上的非线性分类器。SVM的的学习策略就是间隔最大化,SVM的的学习算法就是求解凸二次规划的最优化算法。
支持向量机就像是一条具有宽度的线带对样本进行分类。
软间隔SVM:允许出错,有惩罚
硬间隔SVM:不许出错,
非线性SVM:非线性问题,使用核函数升维划分

2-SVM算法原理-硬间隔SVM
从几何角度来说:对于线性可分的数据集,支持向量机就是找距离正负样本都是最远的超平面,相比感知机,其解是唯一的,且泛化性能更好。如下图所示。

从模型原理:给定线性可分的数据集X,支持向量机希望求得X关于超平面的几何间隔r达到最大的超平面,然后套上sign函数实现分类。
y
=
s
i
g
n
(
W
T
X
+
b
)
=
{
1
,
W
T
+
b
>
0
?
1
,
W
T
+
b
<
0
y=sign(W^TX+b)=\left\{\begin{array}{c} 1,W^T+b>0\\ -1,W^T+b<0 \\ \end{array}\right.
y=sign(WTX+b)={1,WT+b>0?1,WT+b<0?
本质与感知机一样,仍然是在求一个超平面。且几何间隔最大的超平面一定就是距离正负样本都是最远的超平面。
1-间隔与支持向量
给定线性可分的训练集D={(x1,y1),(x2,y2),…,(xm,ym)},划分超平面可通过如下线性方程来描述:
W
T
+
b
=
0
W^T+b=0
WT+b=0
样本空间任意点到超平面距离:
r
=
∣
w
T
+
b
∣
/
∣
∣
w
∣
∣
r=|w^T+b|/||w||
r=∣wT+b∣/∣∣w∣∣
假设超平面能将训练样本正确分类,则令对(xi,yi)有:
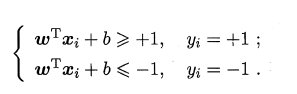
如上所示,距离超平面最近的几个训练样本点使上式的等号成立,它们被称为“支持向量”,两个异类支持向量到超平面的距离之和为:
r
=
2
/
∣
∣
w
∣
∣
r=2/||w||
r=2/∣∣w∣∣

如上图所示,为使r最大,则w需取最小,所以主问题便是:求r的最大值等价于求下式的最小值,同时加上作为约束条件。
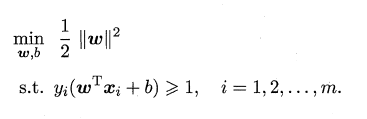
以上公式就是支持向量机(Support Vector Machine,简称SVM) 的基本型,这是一个凸优化问题,故局部极小值就是全局最小值,一般通过拉格朗日方法求解。
2-拉格朗日对偶问题
为了方便求解SVM的主问题,我们将主问题转化为拉格朗日对偶问题。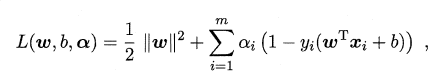
支持向量机的基本型的对偶问题:
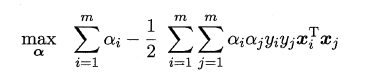
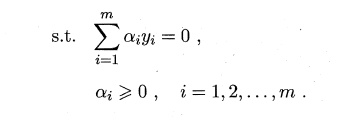
上述过程需满足KKT条件:
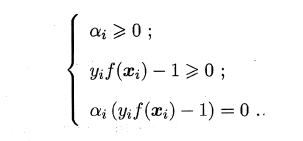
若αi=0,则该样本不会在f(x)的求和中出现,也就不会对f(x)有任何影响;
若αi>0,则必有
y
i
f
(
x
i
)
=
1
y_if(x_i)=1
yi?f(xi?)=1,所对应的样本点位于最大间隔边界上,是一个支持向量。
这显示出支持向量机的一个重要性质:训练完成后,大部分的训练样本都不需要保留,最终模型仅与支持向量有关。
序列最小优化(sequential minimal optimization,SMO):上述问题是二次规划问题,由于需要二次规划算法来求解,该问题的规模正比于训练样本数(因为向量α的维数等于训练样本数),这会在实际问题中造成很大的开销。所以提出了SMO。
3-软间隔与正则化–软间隔SVM
软间隔soft margin:由于我们实际获取的真实样本往往会存在噪声,使得训练数据不是清晰线性可分的,通过允许支持向量机在一些样本上出错,从而缓解该问题。以达到间隔距离和错误之间找到平衡。

允许出错的条件:
在最大化间隔的时候限制不满足间隔大于等于1的样本的个数使之尽可能的少。引入一个惩罚系数C>0,并对每个样本点(xi,yi)引入一个松弛变量(slack variables)ξ≥0。软间隔下新的目标函数:
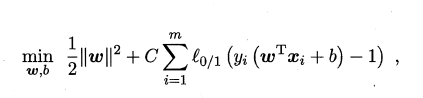
l
0
/
1
l_{0/1}
l0/1?是“0/1损失函数”:
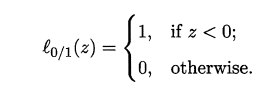
替代损失函数:
l
0
/
1
l_{0/1}
l0/1? 非凸、非连续,数学性质不太好,一般选用替代损失函数。
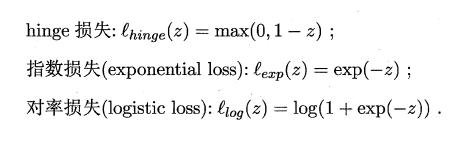 软间隔支持向量机目标函数:
软间隔支持向量机目标函数:
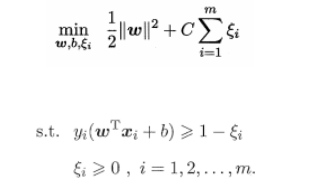
软间隔支持向量机的拉格朗日函数形式:
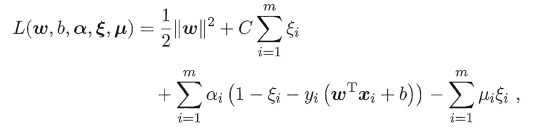
软间隔支持向量机的对偶问题:
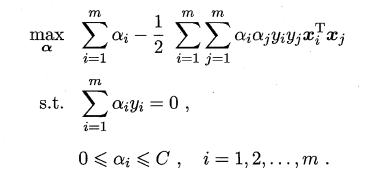
KKT条件
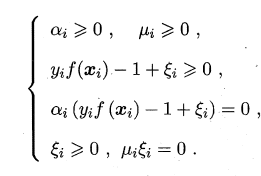
软间隔支持向量机的最终模型仅与支持向量有关,即通过采用hinge 损失函数仍保持了稀疏性。
正则化:可理解为一种"罚函数法"即对不希望得到的结采施以惩罚,从而使得优化过程趋向于希望目标。
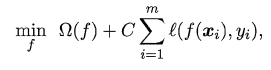
Ω
(
f
)
\Omega (f)
Ω(f)称为“结构风险”,用于描述模型f的某些性质;
第二项
∑
i
=
1
m
l
(
f
(
x
i
)
,
y
i
)
\sum_{i=1}^{m}l(f(x_{i}),y_{i})
∑i=1m?l(f(xi?),yi?)称为“经验风险”,用于描述模型与训练数据的契合程度;
C用于对二者折中。
从另一个角度看,上式也可以称为在“正则化”问题,
Ω
(
f
)
\Omega (f)
Ω(f)称为正则化项,C称为正则化常数。
正则化项:
L
0
L_0
L0?范数
∣
∣
w
∣
∣
2
和
L
1
||w||_2和L_1
∣∣w∣∣2?和L1?范数
∣
∣
w
∣
∣
1
||w||_1
∣∣w∣∣1?倾向于
w
w
w的分量尽量稀疏,即非零分量个数尽量少
L
2
L_2
L2?范数
∣
∣
w
∣
∣
2
||w||_2
∣∣w∣∣2?倾向于w的分量取值尽量均衡,即非零分量个数尽量稠密。
4-核技巧-非线性SVM
核函数:当原始空间出现线性不可分的情况时,将样本从原始空间映射到一个高维的特征空间,使得样本在这个空间内线性可分,升维。如下图所示。

特征空间中划分超平面所对应的模型可表示为:
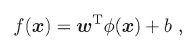
直接计算比较困难,直接定义
k
(
?
,
?
)
k(\cdot ,\cdot )
k(?,?).
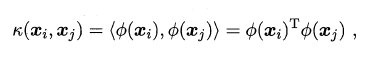
即
x
i
x_{i}
xi?和
x
j
x_{j}
xj?在特征空间的内积等于它们在原始样本空间中通过函数
k
(
?
,
?
)
k(\cdot ,\cdot )
k(?,?)计算的结果。函数
k
(
?
,
?
)
k(\cdot ,\cdot )
k(?,?)就是核函数。
核函数定理:
令X为输入空间,
k
(
?
,
?
)
k(\cdot ,\cdot )
k(?,?)是定义在
X
×
X
X\times X
X×X上的对称矩阵,则k是核函数当且仅当对于任意数据
D
=
{
x
1
,
x
2
,
?
?
,
x
m
}
D=\left \{ x_{1},x_{2},\cdots ,x_{m} \right \}
D={x1?,x2?,?,xm?},核矩阵K总是半正定的:
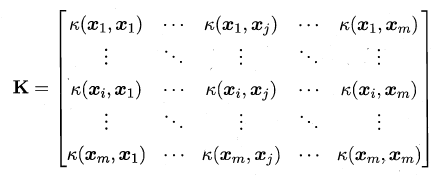
几种常见的核函数:常使用高斯核函数,可以用来表示无穷项。

5-支持向量回归
支持向量回归(Support Vector Regression,SVR):
相比于线性回归用一条线来拟合训练样本,SVR采用
f
(
x
)
=
W
T
+
b
f(x)=W^T+b
f(x)=WT+b为中心,宽度为
2
ε
2\varepsilon
2ε的间隔带,来拟合训练样本。
- 落在带子上的样本<==>线性回归在线上的预测误差为0
- 不在带子上样本的距离为损失<==>LR 均方误差
- 最小化损失迫使带子从最密集穿过,达到拟合训练的目的。
SVR基本形式:
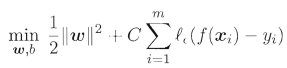
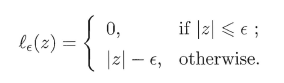
C为正则化常数,
l
ε
l_{\varepsilon }
lε?为
ε
?
\varepsilon -
ε?不敏感损失函数.
SVR目标函数:
其中
ξ
i
,
ξ
j
\xi _{i},\xi _{j}
ξi?,ξj?是松弛变量

SVR的拉格朗日函数形式:
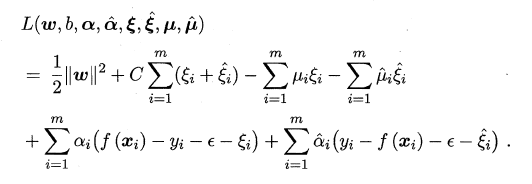
SVR对偶问题:

KKT条件:
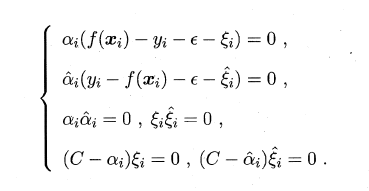
6-后续
后续将使用python代码实现SVM,并使用SVM做一些简单的分类任务。