强化学习(五)—— AlphaGo与Alpha Zero
1. AlphaGo
1.1 论文链接
1.2 输入编码(State)

- 棋盘大小:[19,19]的矩阵, 落子则为1,反之为0。
- Input Shape:[19,19,17]。
- 白棋当前状态及其过去7步的状态:[19,19,1]与[19,19,7]。
- 黑棋当前状态及其过去7步的状态:[19,19,1]与[19,19,7]。
- 当前到谁落子:[19,19,1] (黑棋全为1,白棋全为0)
1.3 训练及评估流程
- 使用behavior cloning 对策略网络进行初步训练;
- 两个策略网络互相对弈,并使用策略梯度对策略网络进行更新;
- 使用策略网络去训练状态价值网络;
- 基于策略网络和价值网络,使用蒙特卡洛树(Monte Carlo Tree Search, MCTS)进行搜索。
1.4 模仿学习(Behavior Cloning)
通过Behavior Cloning从人的经验中初始化策略网络的参数,策略网络的结构为:
随机初始化网络参数后,基于人类对弈的落子序列数据,进行模仿学习(分类任务),使用交叉熵作为损失函数进行参数更新:
- 观测得到状态: s t s_t st?
- 使用策略网络进行预测 p t = [ π ( 1 ∣ s t ; θ ) , π ( 2 ∣ s t ; θ ) , . . . , π ( 361 ∣ s t ; θ ) ] p_t=[\pi(1|s_t;\theta),\pi(2|s_t;\theta),...,\pi(361|s_t;\theta)] pt?=[π(1∣st?;θ),π(2∣st?;θ),...,π(361∣st?;θ)]
- 高级人类玩家采取的动作为 a t ? a_t^* at??
- 策略网络的预测进行one-hot编码后,和人类玩家的动作进行交叉熵计算,并更新网络参数。
模仿学习可认为是循规蹈矩。
1.5 策略网络依据策略梯度进行学习

- 两个策略网络进行对弈直到游戏结束。Player V.S. Opponent,Player 使用策略网络最新的参数,Opponent随机选用过去迭代中的网络参数。
- 得到对弈的序列数据: s 1 , a 1 , s 2 , a 2 , s 3 , a 3 , . . . , s T , a T s_1,a_1,s_2,a_2,s_3,a_3,...,s_T,a_T s1?,a1?,s2?,a2?,s3?,a3?,...,sT?,aT?
- Player获得的回报为: u 1 = u 2 = u 3 = u T ( 赢 了 为 1 , 输 了 为 ? 1 ) u_1=u_2=u_3=u_T(赢了为1,输了为-1) u1?=u2?=u3?=uT?(赢了为1,输了为?1)
- 近似策略梯度(连加) g θ = ∑ t = 1 T ? l o g ( π ( ? ∣ s t ; θ ) ) ? θ ? u t g_\theta=\sum_{t=1}^T \frac{\partial log(\pi(\cdot|s_t;\theta))}{\partial\theta}\cdot u_t gθ?=t=1∑T??θ?log(π(?∣st?;θ))??ut?
- 参数更新 θ ← θ + β ? g θ \theta\gets\theta+\beta\cdot g_{\theta} θ←θ+β?gθ?
1.6 价值网络训练
- 状态价值函数: V π ( S ) = E ( U t ∣ S t = s ) U t = 1 ( w i n ) U t = ? 1 ( f a i l ) V_\pi(S)=E(U_t|S_t=s)\\U_t=1(win)\\U_t=-1(fail) Vπ?(S)=E(Ut?∣St?=s)Ut?=1(win)Ut?=?1(fail)
- 神经网络近似状态价值函数: v ( s ; W ) ~ V π ( s ) v(s;W)\sim V_\pi(s) v(s;W)~Vπ?(s)
- 训练过程:
- 两个策略网络进行对弈直到游戏结束 u 1 = u 2 = u 3 = u T ( 赢 了 为 1 , 输 了 为 ? 1 ) u_1=u_2=u_3=u_T(赢了为1,输了为-1) u1?=u2?=u3?=uT?(赢了为1,输了为?1)
- 损失函数: L = ∑ t = 1 T 1 2 [ v ( s t ; W ) ? u t ] 2 L=\sum_{t=1}^T \frac{1}{2}[v(s_t;W)-u_t]^2 L=t=1∑T?21?[v(st?;W)?ut?]2
- 进行参数更新: W ← W ? α ? ? L ? W W\gets W-\alpha\cdot \frac{\partial L}{\partial W} W←W?α??W?L?
1.7 Monte Carlo Tree Search
每次蒙特卡洛树(MCTS)的搜索过程:
- Selection:假想Player依据当前状态执行一次动作 s t a t s_t\\a_t st?at?
- Expansion: 假想对手做一次动作,并更新状态: s t + 1 s_{t+1} st+1?
- Evaluation: 使用状态价值网络评估得到价值分数: ν = v ( s t + 1 ; W ) \nu=v(s_{t+1};W) ν=v(st+1?;W)假想对弈直到结束,得到奖励: r r r给假想动作进行打分: s c o r e ( a t ) = ν + r 2 score(a_t)=\frac{\nu+r}{2} score(at?)=2ν+r?
- Backup:对动作的分数进行更新。
1.7.1 Selection
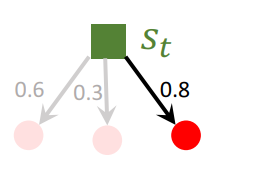
- 观测到状态 s t s_t st?
- 对于所有可选动作,计算其选择分数: s c o r e ( a ) = Q ( a ) + η ? π ( a ∣ s t ; θ ) 1 + N ( a ) {\rm score} (a)=Q(a) + \eta\cdot\frac{\pi(a|s_t;\theta)}{1+N(a)} score(a)=Q(a)+η?1+N(a)π(a∣st?;θ)?Q(a)为通过MRTS得到的动作价值,N(a)为在t时刻状态下已搜索过动作a的次数。
- 具有最高选择分数的动作被选中。
1.7.2 Expansion

由于状态转移函数未知,则用策略函数作为状态转移函数
- 依据策略函数和对手观测到的状态,随机采样得到对手的动作: a t ‘ ~ π ( ? ∣ s t ′ ; θ ) a_t^{‘}\sim \pi(\cdot|s_t^{'};\theta) at‘?~π(?∣st′?;θ)
- 对手的动作将导致新的状态生成: s t + 1 s_{t+1} st+1?
1.7.3 Evaluation

- 重复对弈直至游戏结束,Player的动作: a k ~ π ( ? ∣ s k ; θ ) a_k\sim \pi(\cdot|s_k;\theta) ak?~π(?∣sk?;θ)Opponents的动作: a k ′ ~ π ( ? ∣ s k ′ ; θ ) a_k^{'}\sim \pi(\cdot|s_k^{'};\theta) ak′?~π(?∣sk′?;θ)
- 记录对局结束后的回报: w i n : r T = + 1 l o s e : r T = ? 1 win:r_T=+1\\lose:r_T=-1 win:rT?=+1lose:rT?=?1
- 计算 t+1时刻的状态价值: ν ( s t + 1 ; W ) \nu(s_{t+1};W) ν(st+1?;W)
- t+1时刻状态的价值分数: V ( s t + 1 ) = 1 2 ν ( s t + 1 ; W ) + 1 2 r T V(s_{t+1})=\frac{1}{2}\nu(s_{t+1};W)+\frac{1}{2}r_T V(st+1?)=21?ν(st+1?;W)+21?rT?
1.7.4 Backup

- 对选取t时刻动作后的过程重复多次: a t a_t at?
- t时刻动作的每个子节点对应多条价值分数记录,取平均值更新Q值(在Selection中用到):
Q
(
a
t
)
=
m
e
a
n
(
t
h
e
r
e
c
o
r
d
e
d
V
s
′
)
Q(a_t)=mean(the\quad recorded \quad V^{'}_s)
Q(at?)=mean(therecordedVs′?)

1.8 使用MCTS进行决策
- 动作a被选中的次数为: N ( a ) N(a) N(a)
- 在进行MCTS后,被选中次数最多的动作被Player用于最后决策: a t = a r g m a x a N ( a ) a_t=\mathop{argmax}\limits_{a}N(a) at?=aargmax?N(a)
- 执行完该次决策后,Q值和N值被重置为0: Q ( a ) = 0 N ( a ) = 0 Q(a)=0\\N(a)=0 Q(a)=0N(a)=0
2. AlphaGo Zero
2.1 论文链接
2.2 基于AlphaGo的改进内容
- AlphaGo Zero未使用Behavior cloning(未使用人类经验)
- 策略网络的训练过程中使用MCTS。
2.2 策略网络的训练
AlphaGo Zero使用MCTS训练策略网络
- 观测到状态: s t s_t st?
- 通过策略网络进行预测: p = [ π ( a = 1 ∣ s t , θ ) , . . . , π ( a = 361 ∣ s t , θ ) ] ∈ R 361 p=[\pi(a=1|s_t,\theta),...,\pi(a=361|s_t,\theta)]\in R^{361} p=[π(a=1∣st?,θ),...,π(a=361∣st?,θ)]∈R361
- 通过MCTS进行预测: n = n o r m a l i z e [ N ( a = 1 ) , N ( a = 2 ) , . . . , N ( a = 361 ) ] ∈ R 361 n=normalize[N(a=1),N(a=2),...,N(a=361)]\in R^{361} n=normalize[N(a=1),N(a=2),...,N(a=361)]∈R361
- 计算损失: L = C r o s s E n t r o p y ( n , p ) L=CrossEntropy(n,p) L=CrossEntropy(n,p)
- 对网络参数进行更新: θ ← ? L ? θ \theta \gets \frac{\partial L}{\partial \theta} θ←?θ?L?
3. 代码实现
3.1 策略网络和状态价值网络实现
3.1.1 代码
# -*- coding: utf-8 -*-
# @Time : 2022/4/1 13:47
# @Author : CyrusMay WJ
# @FileName: resnet.py
# @Software: PyCharm
# @Blog :https://blog.csdn.net/Cyrus_May
import tensorflow as tf
import logging
import sys
import os
os.environ["PATH"] += os.pathsep + 'D:\software_root\Anoconda3\envs\AI\Graphviz\\bin' # 用于网络结构画图
class ResidualNet():
def __init__(self,input_dim,output_dim,net_struct,l2_reg=0,logger=None):
"""
:param input_dim:
:param output_dim:
:param net_struct: a list for residual network, net_struct[0] is the first CNN for inputs,
the rest is single block for residual connect. e.g. net_struct = [
{filters:64,kernel_size:(3,3), {filters:128,kernel_size:(3,3),
{filters:128,kernel_size:(3,3)}
]
:param logger:
"""
self.logger=logger
self.input_dim = input_dim
self.output_dim=output_dim
self.l2_reg = l2_reg
self.__build_model(net_struct)
def conv_layer(self,x,filters,kernel_size):
x = tf.keras.layers.Conv2D(filters=filters,
kernel_size=kernel_size,
activation="linear",
padding="same",
data_format="channels_last",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg))(x)
x = tf.keras.layers.BatchNormalization(axis=-1)(x)
x = tf.keras.layers.LeakyReLU()(x)
return x
def residual_block(self,inputs,filters,kernel_size):
x = self.conv_layer(inputs,filters,kernel_size)
x = tf.keras.layers.Conv2D(filters=filters,
kernel_size=kernel_size,
activation="linear",
padding="same",
data_format="channels_last",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg))(x)
x = tf.keras.layers.BatchNormalization(axis=-1)(x)
if inputs.shape[-1] == filters:
x = tf.keras.layers.add([inputs,x])
else:
inputs = tf.keras.layers.Conv2D(filters=filters,
kernel_size=(1,1),
activation="linear",
padding="same",
data_format="channels_last",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg))(inputs)
x = tf.keras.layers.add([inputs, x])
x = tf.keras.layers.LeakyReLU()(x)
return x
def policy_head(self,inputs):
x = tf.keras.layers.Conv2D(filters=2,
kernel_size=(1,1),
activation="linear",
padding="same",
data_format="channels_last",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg))(inputs)
x = tf.keras.layers.Flatten()(x)
x = tf.keras.layers.Dense(units=self.output_dim,
activation="linear",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg),
name="policy_head"
)(x)
return x
def state_value_head(self,inputs):
x = tf.keras.layers.Conv2D(filters=2,
kernel_size=(1, 1),
activation="linear",
padding="same",
data_format="channels_last",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg))(inputs)
x = tf.keras.layers.Flatten()(x)
x = tf.keras.layers.Dense(units=1,
activation="linear",
kernel_regularizer=tf.keras.regularizers.l2(self.l2_reg),
bias_regularizer=tf.keras.regularizers.l2(self.l2_reg),
name="state_value_head"
)(x)
return x
def __build_model(self,net_struct):
input_layer = tf.keras.layers.Input(shape=self.input_dim,name="inputs")
x = self.conv_layer(input_layer,net_struct[0]["filters"],net_struct[0]["kernel_size"])
for i in range(1,len(net_struct)):
x = self.residual_block(x,net_struct[i]["filters"],net_struct[i]["kernel_size"])
v_output = self.state_value_head(x)
p_output = self.policy_head(x)
self.model = tf.keras.models.Model(inputs=input_layer,outputs=[p_output,v_output])
tf.keras.utils.plot_model(self.model, to_file="./AlphZero.png")
self.model.compile(optimizer=tf.optimizers.Adam(),
loss = {"policy_head":tf.nn.softmax_cross_entropy_with_logits,"state_value_head":"mean_squared_error"},
loss_weights={"policy_head":0.5,"state_value_head":0.5})
if __name__ == '__main__':
logger = logging.getLogger(name="ResidualNet")
logger.setLevel(logging.INFO)
screen_handler = logging.StreamHandler(sys.stdout)
screen_handler.setLevel(logging.INFO)
formatter = logging.Formatter('%(asctime)s - %(module)s.%(funcName)s:%(lineno)d - %(levelname)s - %(message)s')
screen_handler.setFormatter(formatter)
logger.addHandler(screen_handler)
residual_net = ResidualNet(logger=logger,input_dim=[19,19,17],
output_dim=19*19,
net_struct=[
{"filters":64,"kernel_size":(3,3)},
{"filters": 128, "kernel_size": (3, 3)},
{"filters": 128, "kernel_size": (3, 3)},
{"filters": 64, "kernel_size": (3, 3)},
{"filters": 64, "kernel_size": (3, 3)},
])
3.1.2 结果

本文部分内容为参考B站学习视频书写的笔记!
by CyrusMay 2022 03 31
摸不到的颜色 是否叫彩虹
看不到的拥抱 是否叫做微风
————五月天(星空)————