[人工智能]计算机视觉（二）--- 局部图像描述

1、Harris角点检测器

概念理解

角点（corner point）对应于物体的拐角，道路的十字路口、丁字路口等。从图像分析的角度来定义角点可以有以下两种定义：

1. 角点可以是两个边缘的角点；
2. 角点是邻域内具有两个主方向的特征点；

• 左图表示一个平坦区域，在各方向移动，窗口内像素值均没有太大变化；
• 中图表示一个边缘特征（Edges），如果沿着水平方向移动(梯度方向)，像素值会发生跳变；如果沿着边缘移动(平行于边缘) ，像素值不会发生变化；
• 右图表示一个角（Corners），不管你把它朝哪个方向移动，像素值都会发生很大变化。

Harris 角点检测算法（也称 Harris & Stephens 角点检测器）。

算法基本思想是使用一个固定窗口在图像上进行任意方向上的滑动，比较滑动前与滑动后两种情况，窗口中的像素灰度变化程度，如果存在任意方向上的滑动，都有着较大灰度变化，那么我们可以认为该窗口中存在角点。

公式推导

其中，不理解泰勒公式的同学，可以去看看这篇文章?

二元函数的泰勒公式_卧新实验室的博客-CSDN博客_二元函数的泰勒公式https://blog.csdn.net/chenqihome9/article/details/86349868

灰度图（离散的二维函数）的一阶微分基本定义是（对于灰度图这样二维数组的图像，它其实就是一个离散的二位函数，说它离散，是因为每个灰度值取值为整数而不是小数，因此?不能无限小，而?的最小单位即是1像素）：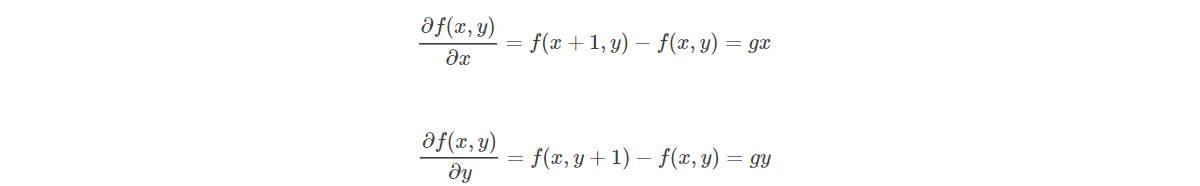

?偏导数的理解偏导数的定义及其计算 - 知乎 (zhihu.com)https://zhuanlan.zhihu.com/p/82470946

上述公式就是利用泰勒展开式对公式进行求解，然后用矩阵的形式进行表达

?

?高中也学过椭圆方程的表达公式，我们转换成矩阵的形式来进行表达，这样就比较容易理解下面这张图像了

系数矩阵M的特征值与椭圆的半轴长短有关

?

平坦区域的像素点，他们的梯度方向虽然各异，但是其幅值都不是很大，所以均聚集在原点附近；边缘区域有一坐标轴分布较散，至于是哪一个坐标上的数据分布较散不能一概而论，这要视边缘在图像上的具体位置而定，如果边缘是水平或者垂直方向，那么Iy轴方向或者Ix方向上的数据分布就比较散；角点区域的x、y方向上的梯度分布都比较分散

通过M的两个特征值的大小对图像进行分类，所以，定义角点相应函数R

?其中??是矩阵的行列式，??是矩阵的迹（主对角线（左上至右下的那一条）上所有元素之和）

代码实践

#调用对应的库
from pylab import *
from numpy import *
#用高斯导数滤波器来计算导数，要在角点检测过程中抑制噪声强度
from scipy.ndimage import filters
from PIL import Image

#在一幅灰度图像中，对每个像素计算 Harris 角点检测器响应函数
#返回像素值为 Harris 响应函数值的一幅图像
def compute_harris_response(im, sigma=3):

    #计算导数
    imx = zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (0, 1), imx)
    imy = zeros(im.shape)
    filters.gaussian_filter(im, (sigma, sigma), (1, 0), imy)

    #  计算 Harris 矩阵的分量
    Wxx = filters.gaussian_filter(imx * imx, sigma)
    Wxy = filters.gaussian_filter(imx * imy, sigma)
    Wyy = filters.gaussian_filter(imy * imy, sigma)

    # 计算特征值和迹
    Wdet = Wxx * Wyy - Wxy ** 2
    Wtr = Wxx + Wyy

    return Wdet / (Wtr * Wtr)
#从这幅图像中挑选出需要的信息。然后，选取像素值高于阈值的所有图像点；再加上额外
#的限制，即角点之间的间隔必须大于设定的最小距离。这种方法会产生很好的角点
#检测结果,避免角点扎堆的现象。
def get_harris_points(harrisim, min_dist=10, threshold=0.6):
    """ 从一幅 Harris 响应图像中返回角点。min_dist 为分割角点和图像边界的最少像素数目 """

    # 寻找高于阈值的候选角点
    corner_threshold = harrisim.max() * threshold
    harrisim_t = (harrisim > corner_threshold) * 1

    # 得到候选点的坐标
    coords = array(harrisim_t.nonzero()).T

    # 以及它们的 Harris 响应值
    candidate_values = [harrisim[c[0], c[1]] for c in coords]

    # 对候选点按照 Harris 响应值进行排序
    index = argsort(candidate_values)

    # 将可行点的位置保存到数组中
    allowed_locations = zeros(harrisim.shape)
    allowed_locations[min_dist:-min_dist, min_dist:-min_dist] = 1

    # 按照 min_distance 原则，选择最佳 Harris 点
    filtered_coords = []
    for i in index:
        if allowed_locations[coords[i, 0], coords[i, 1]] == 1:
            filtered_coords.append(coords[i])
            allowed_locations[(coords[i, 0] - min_dist):(coords[i, 0] + min_dist),
            (coords[i, 1] - min_dist):(coords[i, 1] + min_dist)] = 0

    return filtered_coords

def plot_harris_points(image, filtered_coords):
    """ 绘制图像中检测到的角点 """
    figure()
    gray()
    imshow(image)
    plot([p[1] for p in filtered_coords],
         [p[0] for p in filtered_coords], '.')
    axis('off')
    show()

im=array(Image.open('D:\CV\images\chp2.jpg').convert('L'))
harrisim = compute_harris_response(im)
print("harrisim",harrisim)
filtered_coords = get_harris_points(harrisim,6)
plot_harris_points(im, filtered_coords)

运行结果

opencv-harris角点检测

import cv2
import numpy as np

img = cv2.imread('../images/chp2.jpg')
gray = cv2.cvtColor(img,cv2.COLOR_BGR2GRAY)
gray = np.float32(gray)

#输入图像必须是float32，最后一个参数在0.04到0.05
dst = cv2.cornerHarris(gray,2,3,0.04)
dst = cv2.dilate(dst,None)


# Threshold for an optimal value, it may vary depending on the image.
img [dst>0.01*dst.max()] = [0,0,255]
cv2.imshow('dst',img)
if cv2.waitKey(0) == 27:
    cv2.destroyAllWindows()

运行结果

总结

其中，自己实现的Harris角点的实现和官方的差别还是很大的，其中发现很多时候类似天空，草地等等都容易被识别成角点，具体还得测试一下看看

2、SIFT（尺度不变特征变换）

概念理解

SIFT，即尺度不变特征变换（Scale-invariant feature transform，SIFT），是用于图像处理领域的一种描述方式。这种描述具有尺度不变性，可在图像中检测出关键点，是一种局部特征描述子。

实现步骤

SIFT算法实现特征匹配主要有三个流程，1、提取关键点；2、对关键点附加详细的信息（局部特征），即描述符；3、通过特征点（附带上特征向量的关 键点）的两两比较找出相互匹配的若干对特征点，建立景物间的对应关系。

尺度空间

我们知道人眼对世界的感知有两种特性：一是近大远小：同一物体，近处看时感觉比较大，远处看时感觉比较小；二是"模糊"：更准确说应该是"粗细"，我们看近处，可以看到物体的细节(人会觉得比较清楚)，比如一片树叶，近看可以看到该树叶的纹理，远处看只能看到该片的大概轮廓(人会觉得比较模糊). 从频率的角度出发，图像的细节(比如纹理，轮廓等)代表图像的高频成分，图像较平滑区域表示图像的低频成分.

图像高斯金字塔实际上是一种图像的尺度空间(分线性和非线性空间，此处仅讨论线性空间)，尺度的概念用来模拟观察者距离物体的远近程度，在模拟物体远近的同时，还得考虑物体的粗细程序.

所以就可以理解，尺度空间中各尺度图像的模糊程度逐渐变大，能够模拟人在距离目标由近到远时目标在视网膜上的形成过程。

?高斯金字塔

图像的金字塔模型是指将原始图像不断降阶采样，得到一系列大小不一的图像，由大到小，从下到上构成的塔状模型。原图像为金子塔的第一层，每次降采样所得到的新图像为金字塔的一层(每层一张图像)，每个金字塔共n层。为了让尺度体现其连续性，高斯金字塔在简单降采样的基础上加上了高斯滤波。如上图所示，将图像金字塔每层的一张图像使用不同参数做高斯模糊，Octave表示一幅图像可产生的图像组数，Interval表示一组图像包括的图像层数。另外，降采样时，高斯金字塔上一组图像的初始图像(底层图像)是由前一组图像的倒数第三张图像隔点采样得到的。

关键点检测——DOG

代码实践

from PIL import Image
import os
from pylab import *

""" 处理一幅图像，然后将结果保存在文件中 """

def process_image(imagename, resultname, params="--edge-thresh 10 --peak-thresh 5"):

    if imagename[-3:] != 'pgm':
        # create a pgm file
        im = Image.open(imagename).convert('L')
        im.save('tmp.pgm')
        imagename = 'tmp.pgm'

    cmmd = str("sift " + imagename + " --output=" + resultname +
               " " + params)
    os.system(cmmd)
    print('processed', imagename, 'to', resultname)

""" 读取特征属性值，然后将其以矩阵的形式返回 """
def read_features_from_file(filename):

    f = loadtxt(filename)
    return f[:, :4], f[:, 4:]  # feature locations, descriptors

""" 将特征位置和描述子保存到文件中 """
def write_features_to_file(filename, locs, desc):
    savetxt(filename, hstack((locs, desc)))


""" 显示带有特征的图像
 输入：im（数组图像），locs（每个特征的行、列、尺度和朝向）"""
def plot_features(im, locs, circle=False):


    def draw_circle(c, r):
        t = arange(0, 1.01, .01) * 2 * pi
        x = r * cos(t) + c[0]
        y = r * sin(t) + c[1]
        plot(x, y, 'b', linewidth=2)

    imshow(im)
    if circle:
        for p in locs:
            draw_circle(p[:2], p[2])
    else:
        plot(locs[:, 0], locs[:, 1], 'ob')
    axis('off')


imname = 'D:\CV\images\chp2.jpg'
im1 = array(Image.open(imname).convert('L'))
process_image(imname,'chp2.sift')
l1,d1 = read_features_from_file('chp2.sift')
figure()
gray()
plot_features(im1,l1,circle=True)
show()

运行结果

""" 对于第一幅图像中的每个描述子，选取其在第二幅图像中的匹配
 输入：desc1（第一幅图像中的描述子），desc2（第二幅图像中的描述子）"""

def match(desc1, desc2):

    desc1 = array([d / linalg.norm(d) for d in desc1])
    desc2 = array([d / linalg.norm(d) for d in desc2])

    dist_ratio = 0.6
    desc1_size = desc1.shape

    matchscores = zeros((desc1_size[0]), 'int')
    desc2t = desc2.T # 预先计算矩阵转置
    for i in range(desc1_size[0]):
        dotprods = dot(desc1[i, :], desc2t) # 向量点乘
        dotprods = 0.9999 * dotprods
        # 反余弦和反排序，返回第二幅图像中特征的索引
        indx = argsort(arccos(dotprods))

        # 检查最近邻的角度是否小于 dist_ratio 乘以第二近邻的角度
        if arccos(dotprods)[indx[0]] < dist_ratio * arccos(dotprods)[indx[1]]:
            matchscores[i] = int(indx[0])

    return matchscores


def appendimages(im1, im2):

    rows1 = im1.shape[0]
    rows2 = im2.shape[0]

    if rows1 < rows2:
        im1 = concatenate((im1, zeros((rows2 - rows1, im1.shape[1]))), axis=0)
    elif rows1 > rows2:
        im2 = concatenate((im2, zeros((rows1 - rows2, im2.shape[1]))), axis=0)


    return concatenate((im1, im2), axis=1)


def plot_matches(im1, im2, locs1, locs2, matchscores, show_below=True):

    im3 = appendimages(im1, im2)
    if show_below:
        im3 = vstack((im3, im3))

    # show image
    imshow(im3)

    # draw lines for matches
    cols1 = im1.shape[1]
    for i, m in enumerate(matchscores):
        if m > 0:
            plot([locs1[i][1], locs2[m][1] + cols1], [locs1[i][0], locs2[m][0]], 'c')
    axis('off')

""" 双向对称版本的 match()"""
def match_twosided(desc1, desc2):

    matches_12 = match(desc1, desc2)
    matches_21 = match(desc2, desc1)

    ndx_12 = matches_12.nonzero()[0]

    # remove matches that are not symmetric
    for n in ndx_12:
        if matches_21[int(matches_12[n])] != n:
            matches_12[n] = 0

    return matches_12


imname1 = 'D:\CV\images\chp2-3.jpg'
im1 = array(Image.open(imname1).convert('L'))
process_image(imname1,'chp2-3.sift')
l1,d1 = read_features_from_file('chp2-3.sift')

# figure()
# gray()
# subplot(121)
# plot_features(im1,l1,circle=False)

imname2 = 'D:\CV\images\chp2-5.jpg'
im2 = array(Image.open(imname2).convert('L'))
process_image(imname2,'chp2-5.sift')
l2,d2 = read_features_from_file('chp2-5.sift')
# subplot(122)
# plot_features(im2,l2,circle=False)
# show()

matches=match_twosided(d1,d2)
figure(dpi=180)
gray()
subplot(121)
plot_matches(im1,im2,l1,l2,matches,show_below=True)
show()

?

3、匹配地理标记图像

#-*- coding: utf-8 -*-
from pylab import *
from PIL import Image
from pcv.localdescriptors import sift
from pcv.tools import imtools
import pydot

download_path = "D:\CV\images"  # set this to the path where you downloaded the panoramio images
path = "D:\CV\images"  # path to save thumbnails (pydot needs the full system path)
#list of downloaded filenames
imlist = imtools.get_imlist(download_path)
nbr_images = len(imlist)
#extract features
featlist = [imname[:-3] + 'sift' for imname in imlist]
for i, imname in enumerate(imlist):
    sift.process_image(imname, featlist[i])

matchscores = zeros((nbr_images, nbr_images))

for i in range(nbr_images):
    for j in range(i, nbr_images):  # only compute upper triangle
        print ('comparing ', imlist[i], imlist[j])
        l1, d1 = sift.read_features_from_file(featlist[i])
        l2, d2 = sift.read_features_from_file(featlist[j])
        matches = sift.match_twosided(d1, d2)
        nbr_matches = sum(matches > 0)
        print ('number of matches = ', nbr_matches)
        matchscores[i, j] = nbr_matches
print ("The match scores is: \n", matchscores)

#copy values
for i in range(nbr_images):
    for j in range(i + 1, nbr_images):  # no need to copy diagonal
        matchscores[j, i] = matchscores[i, j]

#可视化

threshold = 2  # min number of matches needed to create link

g = pydot.Dot(graph_type='graph')  # don't want the default directed graph

for i in range(nbr_images):
    for j in range(i + 1, nbr_images):
        if matchscores[i, j] > threshold:
            # first image in pair
            im = Image.open(imlist[i])
            im.thumbnail((100, 100))
            filename = path + str(i) + '.png'
            im.save(filename)  # need temporary files of the right size
            g.add_node(pydot.Node(str(i), fontcolor='transparent', shape='rectangle', image=filename))

            # second image in pair
            im = Image.open(imlist[j])
            im.thumbnail((100, 100))
            filename = path + str(j) + '.png'
            im.save(filename)  # need temporary files of the right size
            g.add_node(pydot.Node(str(j), fontcolor='transparent', shape='rectangle', image=filename))

            g.add_edge(pydot.Edge(str(i), str(j)))
g.write_png('b.png')

?遇到了这个问题，暂时没解决！