1初始种群的产生
低维单目标优化产生初始种群的编码采取二进制编码方式,在产生初始种群之前,要确定染色体的基因数目,这是由算法想达到的精度决定的(但在不知道精度的时候也可以自己定义),如果要求最终求得的决策变量精确为5,根据公式: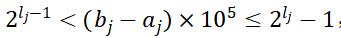
,即可确定该决策变量需要的基因数l_j,其中b_j,a_j为该决策变量取值的上下界,一个个体所需的基因数目L为所有决策变量对应的l_j之和。在基因数目确定了之后,即可产生初始种群,采取二进制编码随机生成的方式。而二进制解码根据公式: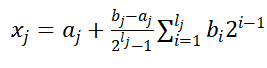
。而针对高维单目标优化产生初始种群的编码采取浮点数编码方式,在(a_j,b_j)中随机选择浮点数。
2适应度函数
在遗传算法中,规定适应值越大的染色体越优。因此对于一些求解最大值的数值优化问题,我们可以直接套用问题定义的函数表达式。但是对于其他优化问题,问题定义的目标函数表达式必须经过一定的变换。
通过画图,发现所选择的单目标优化问题都是在求解最小值。因此,在以上几个最小化的函数中,f函数值越小说明其适应能力越强。为了符合常规习惯,将求 f 最小值的问题转化为求 -f 的最大值,那么适应度评价函数即为 -f, 其值越大,适应能力越强,越应该被保留。
3遗传算子的确定
对于选择步骤,采取轮盘赌选择,其思想是适应度更大的个体更大概率会被保留。
对于交叉步骤,采用单点交叉方式,交叉算子设置为0.8(高维是0.6),交叉是针对个体而言的,如果随机产生的概率小于0.75,则该个体可以参与交叉,随机与另外一个个体交叉,生成新的子代。
对于变异步骤,采用单点变异,变异算子设置为0.01,变异是针对染色体的每个基因而言的,如果随机产生的概率小于0.01,则该基因位发生变异,0和1互换(高维则是在(a_j,b_j))随机选择一个概率小于0.01的值)。
4终止条件
若算法满足终止条件(低维单目标优化是最小迭代100且持续200代最优值改变小于1e-8,高维单目标优化是迭代1000),则输出最优的染色体及其适应度值,该适应度值作为本题的解;否则,返回第二步继续执行。
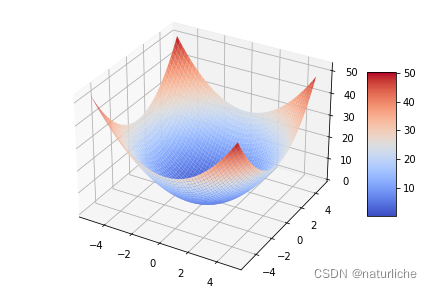
![二维球形函数:x, y ∈ [ ? 5.12,5.12], f_1(x, y) = x^2 + y^2](https://img-blog.csdnimg.cn/065a2c7b4a50407a943311b240feafc0.png)
# -*- coding: utf-8 -*-
"""
Created on Sat Mar 26 19:13:16 2022
@author: Baum
"""
#种群初始化
import random
import math
import matplotlib.pyplot as plt
import numpy as np
from mpl_toolkits.mplot3d import Axes3D
#种群初始化:
#1.计算每一维变量的区间长度和精度产生的染色体长度
def cal_dim_size(x_y_bound,decimals):
copies = (x_y_bound[1]-x_y_bound[0])*10**decimals
x_y_size = 1
while 2**(x_y_size -1) < copies:
if copies < 2**x_y_size - 1:
break
x_y_size += 1
return x_y_size
#2.二进制变为十进制实数(处于取值区间)
'''
#这里的pop是指其中一个个体的一个维度的计算
def binary_to_decimal(x_y_bound,x_y_size,pop_individual_half):
#pop如果直接写成010这样的形式,则是无效的,且np产生的是numpy需要转为list再转为str
pop_str = ''.join(str(x) for x in pop_individual_half)
#np.around求一个确定精度的数
return np.around(x_y_bound[0]+ int(pop_str,2)*(x_y_bound[1]-x_y_bound[0])
/(2**x_y_size-1),decimals=decimals)
'''
#给一整个pop
def binary_to_decimal(x_y_bound,x_y_size,pop):
pop_decimal = []
for i in range(pop.shape[0]):
pop_individual = pop[i]
pop_result1 = []
for j in range(0,len(pop[i]),x_y_size):
pop_individual_half = ''.join(str(x) for x in pop_individual[j:j+x_y_size])
#np.around求一个确定精度的数
pop_result = np.around(x_y_bound[0]+ int(pop_individual_half,2)*(x_y_bound[1]-x_y_bound[0])
/(2**x_y_size-1),decimals=decimals)
pop_result1.append(pop_result)
#print(pop_result1)
pop_decimal.append(pop_result1)
return pop_decimal
'''
#适应度评估:发现函数优化过程均需要求得函数在可行域中的最小值
def git_fitness(x,y):
return -1*(x**2+y**2)
'''
def get_fitness(pop_decimal):
fitness = []
#求解每一个个体的fitness然后形成数组
for i in range(np.array(pop_decimal).shape[0]):
git_fitness = -1*(pop_decimal[i][0]**2+pop_decimal[i][1]**2)
fitness.append(git_fitness)
return fitness
def cumulative_pro_select(fitness,pop):
fitness_sum = np.sum(np.array(fitness))
#求累积的适应度
q_k = [0]*len(fitness)
p_k = np.divide(np.array(fitness),fitness_sum)
for i in range(len(p_k)):
q_k[i] = np.sum(p_k[0:i+1])
#找它在q_k中第一个小于的数
select_idex = []
r = np.random.random(size = (len(q_k),1))
for i in range(len(q_k)):
for j in range(len(q_k)):
if r[i] <= q_k[j]:
idex = j
break
select_idex.append(idex)
'''
print(fitness)
print(r)
print(q_k)
'''
#print(select_idex)
#返回长度为种群大小
pop_new = []
for m in range(len(q_k)):
pop_idex = select_idex[m]
pop_new.append(pop[pop_idex])
return np.array(pop_new)
def crossover(pop_new,pc):
pop_new1 = pop_new.copy()
for i in range(0,len(pop_new1),2):
r = np.random.random()
if r <= pc:
#进行交叉
cross_position = np.random.randint(0,len(pop_new1))
#print("cross_position:",cross_position)
pop_new1_ts = pop_new1[i][cross_position:].copy()
#print("pop_new1_ts",pop_new1_ts)
pop_new1[i][cross_position:] = pop_new1[i+1][cross_position:].copy()
pop_new1[i+1][cross_position:] = pop_new1_ts.copy()
#print("pop_new1[i+1][cross_position:]",pop_new1[i+1][cross_position:])
else:
pop_new1[i] = pop_new1[i].copy()
pop_new1[i+1] = pop_new1[i+1].copy()
pop_new_cross = pop_new1.copy()
return np.array(pop_new_cross)
#存在的问题关于array赋值https://blog.csdn.net/C_Dreams/article/details/79197612
def mutation(pop_new_cross,pm):
r = np.random.random(size = (len(pop_new_cross),len(pop_new_cross[0])))
for i in range(len(pop_new_cross)):
for j in range(len(pop_new_cross[0])):
if r[i][j] <= pm:
pop_new_cross[i][j] = (pop_new_cross[i][j]+1)%2
else:
pop_new_cross[i][j] = pop_new_cross[i][j]
pop_new_cross_mutation = pop_new_cross.copy()
return pop_new_cross_mutation
if __name__ == "__main__":
#参数设置
x_y_bound = [-5.12,5.12]#因为式子里面xy取值范围一样
decimals = 5
y_precision = 6
population_size = 66
pc = 0.8
pm = 0.01
max_generation = 1000
min_generation = 100
without_optim_tolerate = 200
# 如果持续200代最优值改善很小(1e-6)的话,提前终止迭代
x_y_size = cal_dim_size(x_y_bound,decimals)
chromosome_size = x_y_size*2
#产生整个种群,pop是population_size*chromosome_size的数组
pop = np.random.randint(2,size=(population_size,chromosome_size))
#二维球性函数
plt.ion() # 打开plt交互模式
fig = plt.figure()
ax = Axes3D(fig)
X = np.arange(x_y_bound[0], x_y_bound[1], (x_y_bound[1] - x_y_bound[0])/50)
Y = np.arange(x_y_bound[0], x_y_bound[1], (x_y_bound[1] - x_y_bound[0])/50)
X, Y = np.meshgrid(X, Y)
Z = X**2+Y**2
# 绘制3D曲面
surf = ax.plot_surface(X, Y, Z, rstride=1, cstride=1, cmap='coolwarm')
fig.colorbar(surf, shrink=0.5, aspect=5)
plt.title("Two dimensional spherical",y=-0.1)
plt.savefig('tow_dim.png')
#plt.show()
best_F = float('-inf')
worse_F = float('inf')
mean_F = float('inf')
best_x, best_y = 0, 0
actual_generation = 0
cur_best_F_list = []
best_F_list = []
cur_worse_F_list = []
cur_mean_F_list = []
#迭代进化
for i in range(max_generation):
pop_decimal = binary_to_decimal(x_y_bound,x_y_size,pop)
fitness = get_fitness(pop_decimal)
#返回最大值所对应的索引
#这里应该记录的是十进制DNA表示->需要找到fitness最大值,这里是真实值
cur_best_x = pop_decimal[np.argmax(fitness)][0]
cur_best_y = pop_decimal[np.argmax(fitness)][1]
print("generation:", i + 1)
print("most fitted DNA: ", pop[np.argmax(fitness)])
print("var corresponding to most fitted DNA: ", cur_best_x, cur_best_y)
print("F_values corresponding to DNA: ", -1 * fitness[np.argmax(fitness)])
if fitness[np.argmax(fitness)] > best_F:
best_F = fitness[np.argmax(fitness)] #这里是负数
best_x = cur_best_x
best_y = cur_best_y
if fitness[np.argmax(fitness)] < worse_F:
worse_F = fitness[np.argmax(fitness)]
# 判断是否需要提前终止迭代
if i+1 > min_generation and (best_F - best_F_list[i - (without_optim_tolerate if i > without_optim_tolerate else i)]) < 10 ** (-8):
actual_generation = i+1
break
# 逐代绘制,绘制前先清除上一代的
if sca in globals():
globals.remove(sca)
sca = ax.scatter(best_x, best_y, fitness[np.argmax(fitness)], s=200, lw=0, c='red', alpha=0.5)
plt.pause(0.001)
pop_new = cumulative_pro_select(fitness,pop)
pop_new_cross = crossover(pop_new,pc)
pop_new_cross_mutation = mutation(pop_new_cross,pm)
pop = pop_new_cross_mutation.copy()
mean_F = np.mean(fitness)
cur_mean_F_list.append(mean_F)
cur_best_F_list.append(fitness[np.argmax(fitness)]) #这里全为负数
cur_worse_F_list.append(fitness[np.argmin(fitness)])
best_F_list.append(best_F)
actual_generation = i+1
# 迭代完输出最优值和对应的决策变量
print("best F_value is", -1 * best_F)
print("var corresponding to best F_value is", best_x, best_y)
plt.ioff()
plt.show()
# 绘制进化代数和最优解的关系图
best_F_list = -1 * np.array(best_F_list) #这里开始全部变为正数
cur_best_F_list = -1 * np.array(cur_best_F_list)
cur_worse_F_list = -1 * np.array(cur_worse_F_list)
cur_mean_F_list = -1 * np.array(cur_mean_F_list)
plt.plot(range(actual_generation - 1), best_F_list, label='best solution so far', color='blue')
plt.plot(range(actual_generation - 1), cur_best_F_list, label='best solution of current generation', color='pink')
plt.plot(range(actual_generation - 1), cur_worse_F_list, label='worse solution of current generation', color='green')
plt.plot(range(actual_generation - 1), cur_mean_F_list, label='mean solution of current generation', color='yellow')
# 每隔50代标注一下最优值
l = [i for i in range(actual_generation-1) if i % 50 == 0]
for x, y in zip(l, best_F_list[l]):
print(x + 1, y)
plt.text(x, y + 0.001, f'%.{y_precision}f' % y, ha='center', va= 'bottom',fontsize=12)
# 参数标注
plt.text(actual_generation * 0.5, (best_F + worse_F) / -2, "pc=%.2f, pm=%.2f, actual_generation=%d" % (pc, pm, actual_generation), fontdict={'size': 15, 'color': 'black'})
plt.legend(loc='best', fontsize=20)
plt.title('generation vs. F_value of f1', fontsize=25, color='black')
plt.xticks(fontsize=20)
plt.yticks(fontsize=20)
fig = plt.gcf()
fig.set_size_inches(18, 10)
plt.savefig('f1_generation_F_value.png')
plt.show()
结果
在迭代了358代后收敛,下表为迭代结束后的结果,在x=0.06812,y=-0.06324处取得最优值0.008640,基本收敛到精确解0。图3蓝色线显示到当前代为止的最好适应度值,粉色线显示在当前这一代的最好适应度值,绿色线显示在当前这一代最坏适应度值,黄色线显示在当前这一代平均适应度值。
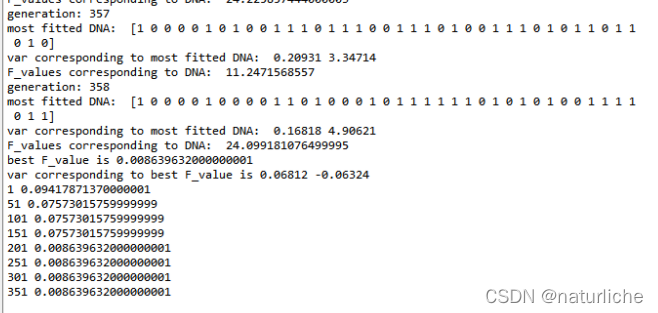
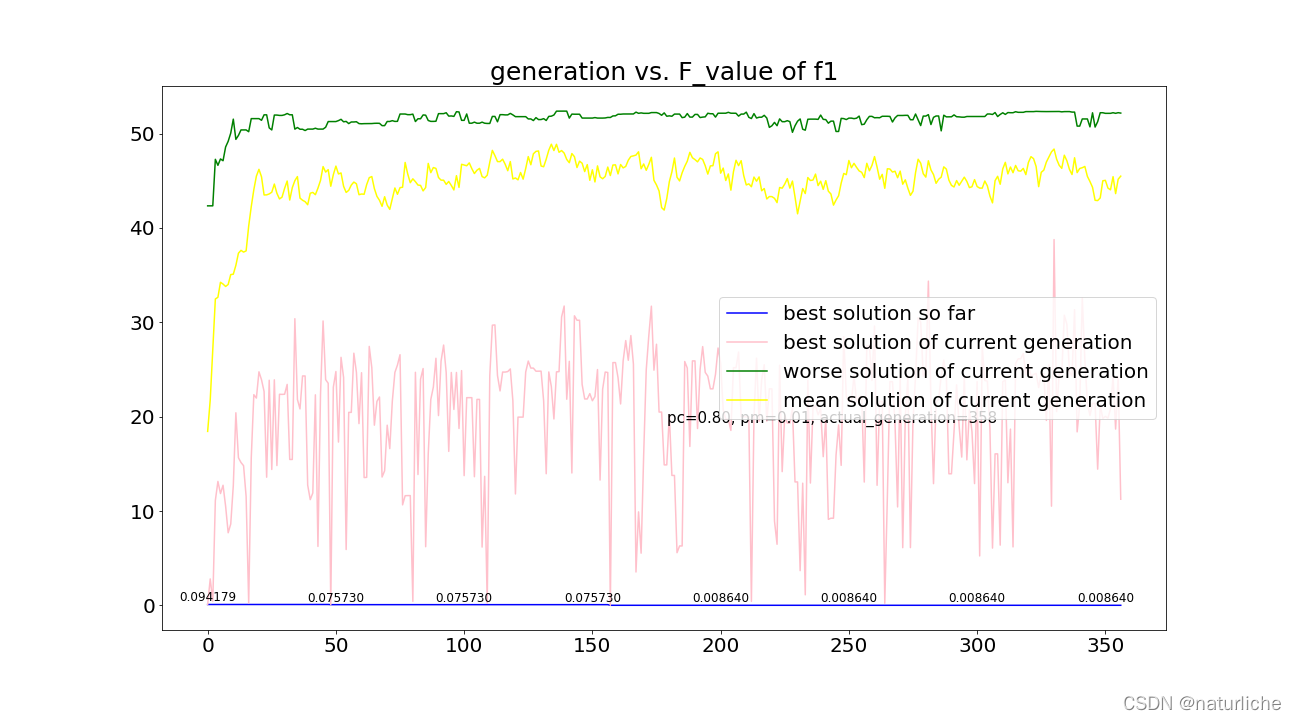
虽然感觉最后好像结果有点不对