文章目录
朴素贝叶斯

- 高斯朴素贝叶斯(GaussianNB)
# 高斯朴素贝叶斯GaussianNB
# class sklearn.naive_bayes.GaussianNB (priors=None, var_smoothing=1e-09)
from sklearn.naive_bayes import GaussianNB
gnb = GaussianNB().fit(Xtrain,Ytrain)
acc_score = gnb.score(Xtest,Ytest)#查看分数
Y_pred = gnb.predict(Xtest) #查看预测结果
prob = gnb.predict_proba(Xtest) #查看预测的概率结果
- 多项式朴素贝叶斯MultinomialNB
# 多项式朴素贝叶斯MultinomialNB
#多项式分布擅长的是分类型变量(TF-IDF向量技术 和 单词计数向量)
from sklearn.preprocessing import MinMaxScaler
from sklearn.naive_bayes import MultinomialNB
#先归一化,保证输入多项式朴素贝叶斯的特征矩阵中不带有负数
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
mnb = MultinomialNB().fit(Xtrain_, Ytrain)
#一些传统的接口
mnb.predict(Xtest_)
mnb.predict_proba(Xtest_)
mnb.score(Xtest_,Ytest)
brier_score_loss(Ytest,mnb.predict_proba(Xtest_)[:,1],pos_label=1)
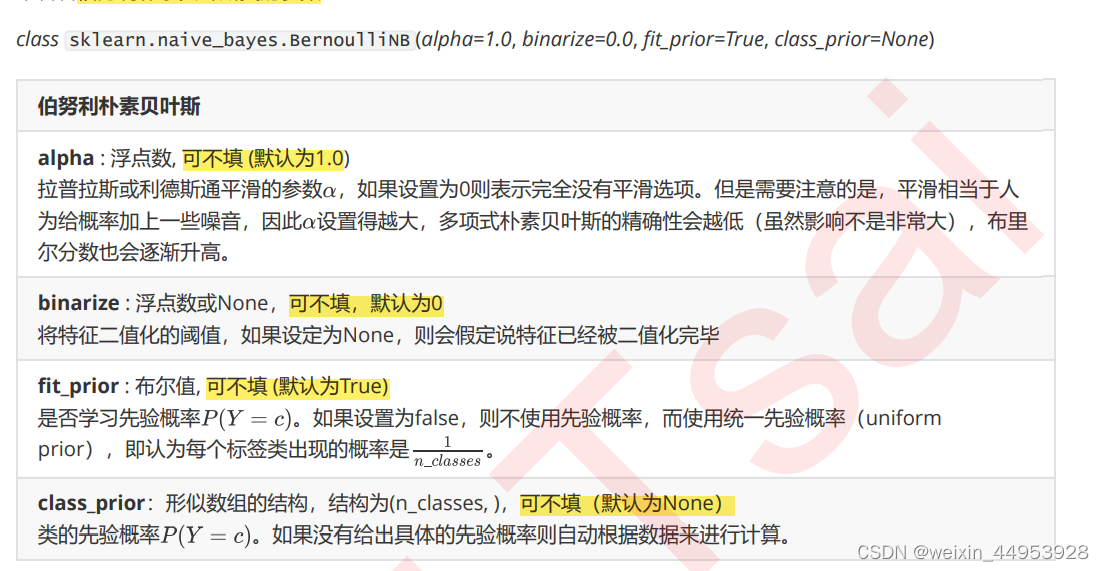
- 伯努利朴素贝叶斯BernoulliNB
# 伯努利朴素贝叶斯BernoulliNB
# 由于伯努利朴素贝叶斯是处理二项分布,所以它更加在意的是“存在与否”,
#而不是“出现多少次”这样的次数或频率,这是伯努利贝叶斯与多项式贝叶斯的根本性不同
# class sklearn.naive_bayes.BernoulliNB (alpha=1.0, binarize=0.0, fit_prior=True, class_prior=None)
from sklearn.naive_bayes import BernoulliNB
mms = MinMaxScaler().fit(Xtrain)
Xtrain_ = mms.transform(Xtrain)
Xtest_ = mms.transform(Xtest)
#不设置二值化
bnl_ = BernoulliNB().fit(Xtrain_, Ytrain)
bnl_.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl_.predict_proba(Xtest_)[:,1],pos_label=1)
#设置二值化阈值为0.5
bnl = BernoulliNB(binarize=0.5).fit(Xtrain_, Ytrain)
bnl.score(Xtest_,Ytest)
brier_score_loss(Ytest,bnl.predict_proba(Xtest_)[:,1],pos_label=1)
- 补集朴素贝叶斯ComplementNB
# 补集朴素贝叶斯ComplementNB(是标准多项式朴素贝叶斯算法的改进)
# class sklearn.naive_bayes.ComplementNB (alpha=1.0, fit_prior=True, class_prior=None, norm=False)
from sklearn.naive_bayes import ComplementNB
clf=ComplementNB()
clf.fit(Xtrain,Ytrain)
y_pred = clf.predict(Xtest)
proba = clf.predict_proba(Xtest)[:,1]
score = clf.score(Xtest,Ytest)
2、 不同分布下的贝叶斯
二、高斯朴素贝叶斯(GaussianNB)


贝叶斯是速度很快,但分类效果一般,并且初次训练之后的结果就很接近算法极限的算法,几乎没有调参的余地。也就是说,如果我们追求对概率的预测,并且希望越准确好,那我们应该先选择逻辑回归。
如果数据十分复杂,或者是稀疏矩阵,那我们坚定地使用贝叶斯。如果我们分类的目标不是要追求对概率的预测,那我们完全可以先试试看高斯朴素贝叶斯的效果(反正它运算很快速,还不需要太多的样本),如果效果很不错,我们就很幸运地得到了一个表现优秀又快速的模型。如果我们没有得到比较好的结果,那我们完全可以选择再更换成更加复杂的模型。



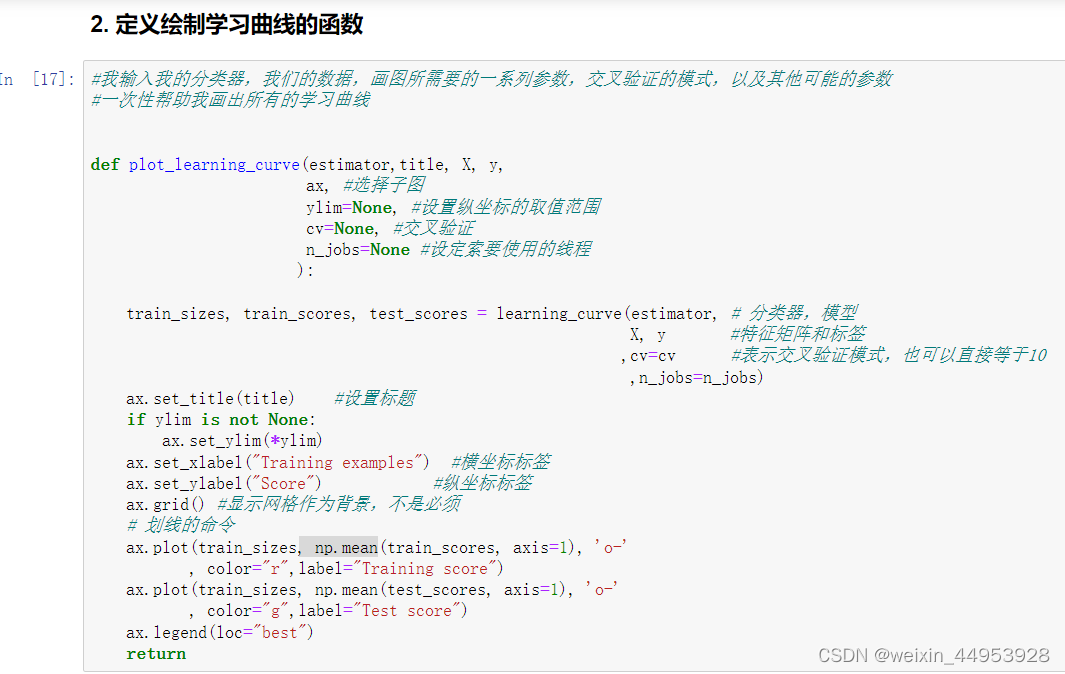
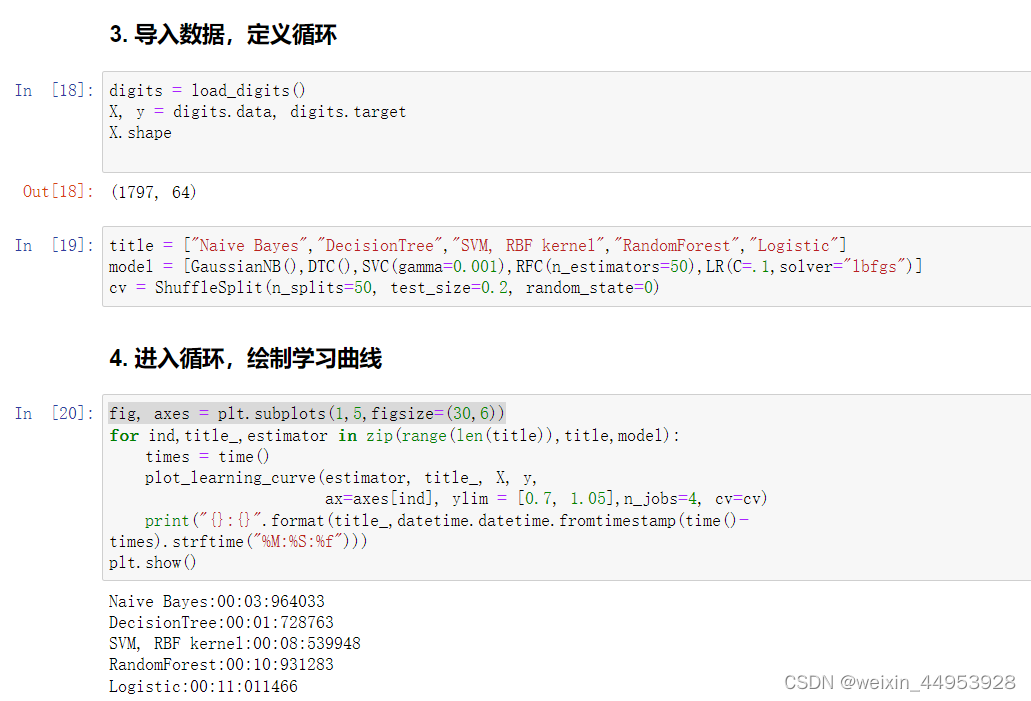
2.1.2 探索贝叶斯:高斯朴素贝叶斯的拟合效果与运算速度


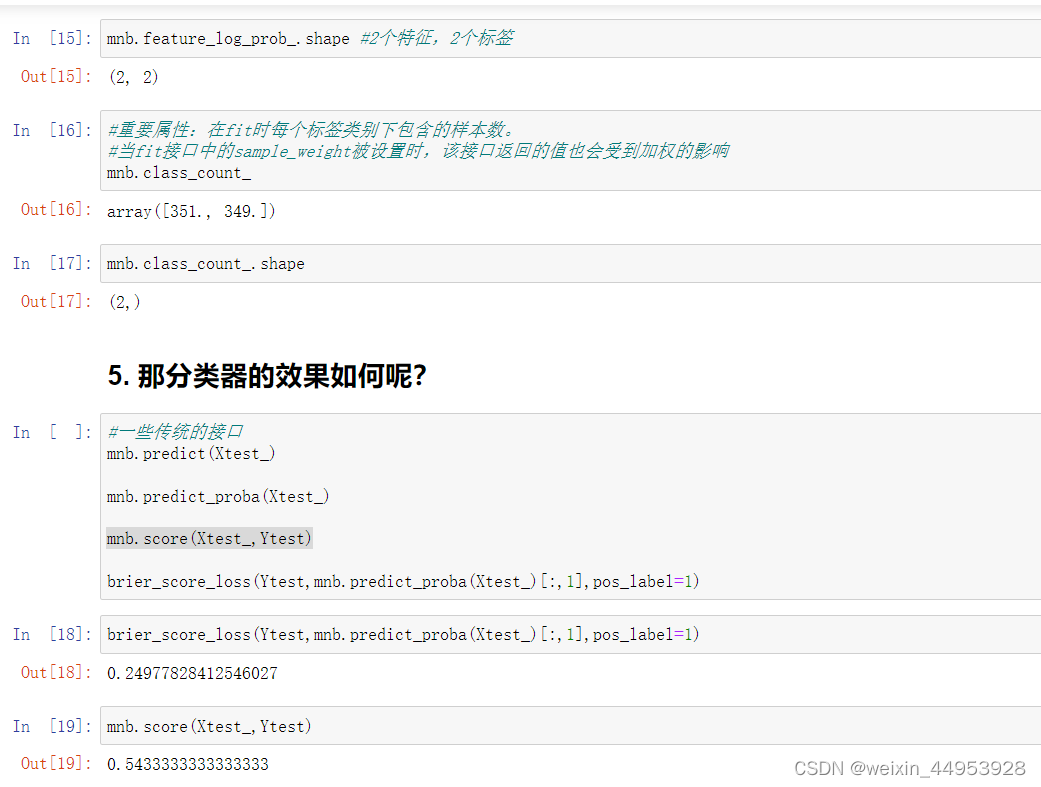
三、多项式朴素贝叶斯MultinomialNB

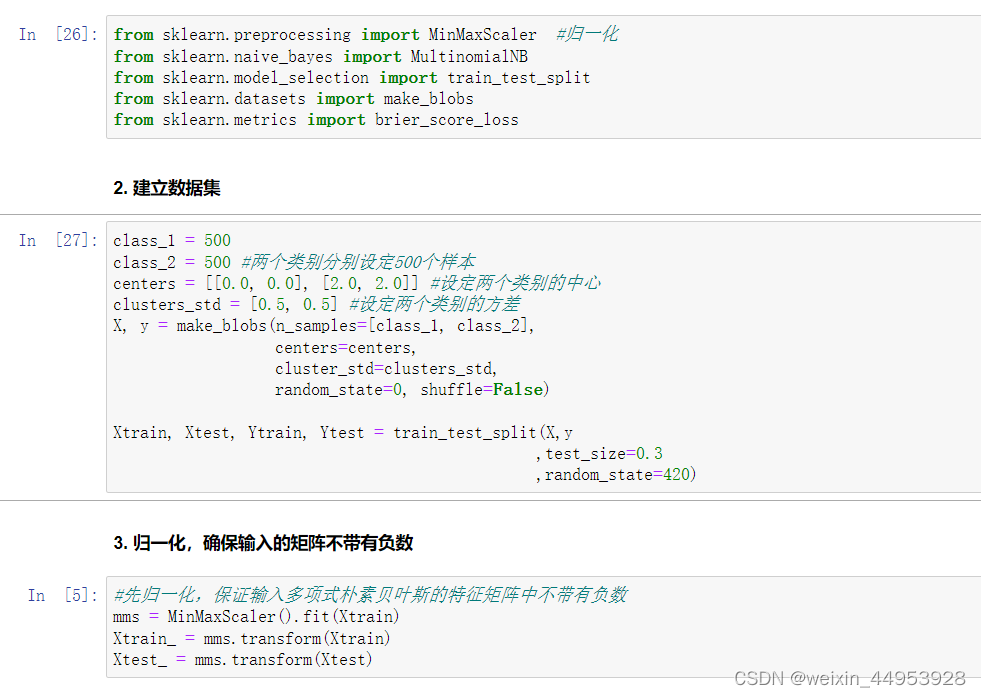
class sklearn.naive_bayes.MultinomialNB (alpha=1.0, fit_prior=True, class_prior=None)


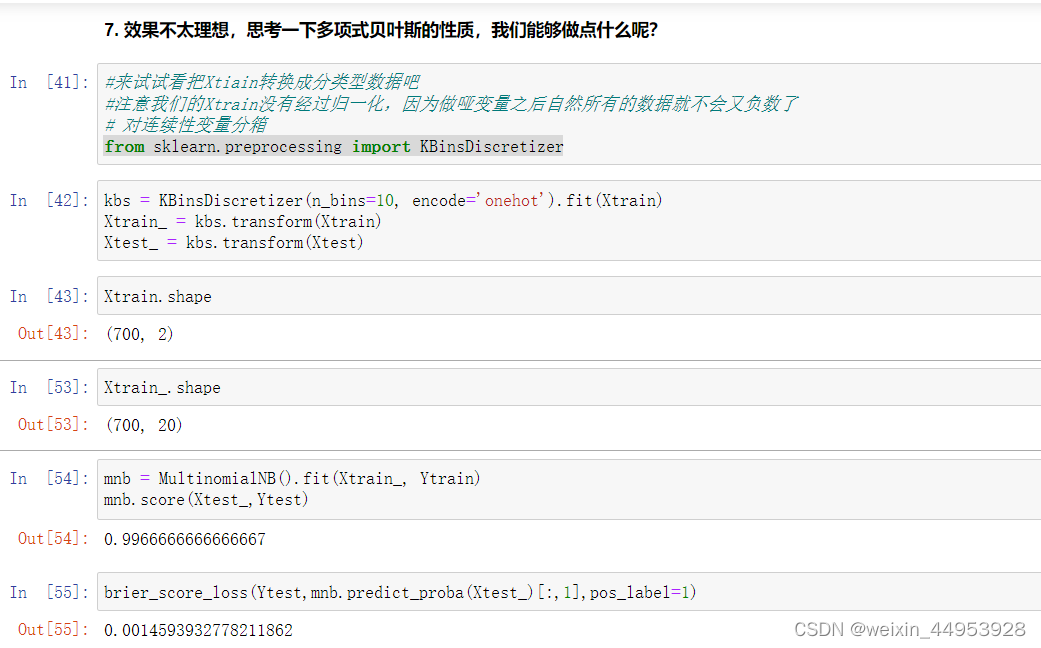
四、伯努利朴素贝叶斯BernoulliNB
多项式朴素贝叶斯可同时处理二项分布(抛硬币)和多项分布(掷骰子),其中二项分布又叫做伯努利分布,它是一种现实中常见,并且拥有很多优越数学性质的分布。因此,既然有着多项式朴素贝叶斯,我们自然也就又专门用来处理二项分布的朴素贝叶斯:伯努利朴素贝叶斯
伯努利朴素贝叶斯与多项式朴素贝叶斯非常相似,都常用于处理文本分类数据。但由于伯努利朴素贝叶斯是处理二项分布,所以它更加在意的是“存在与否”,而不是“出现多少次”这样的次数或频率,这是伯努利贝叶斯与多项式贝叶斯的根本性不同。在文本分类的情况下,伯努利朴素贝叶斯可以使用单词出现向量(而不是单词计数向量)来训练分类器。文档较短的数据集上,伯努利朴素贝叶斯的效果会更加好。如果时间允许,建议两种模型都试试看。

五、 探索贝叶斯:贝叶斯的样本不均衡问题
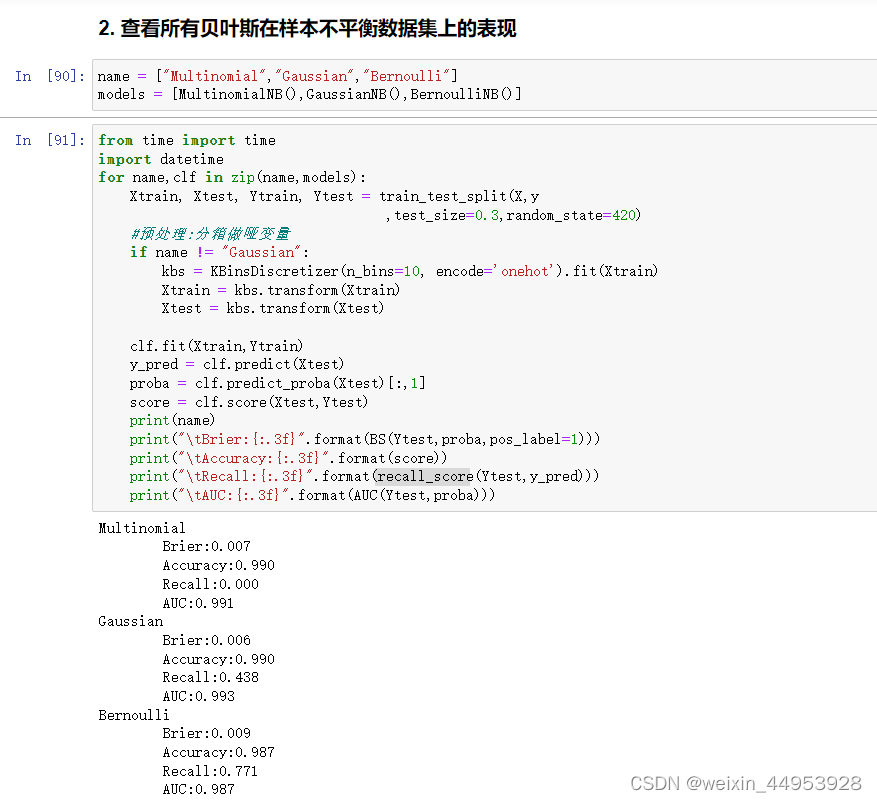
从结果上来看,多项式朴素贝叶斯判断出了所有的多数类样本,但放弃了全部的少数类样本,受到样本不均衡问题影响最严重。高斯比多项式在少数类的判断上更加成功一些,至少得到了43.8%的recall。伯努利贝叶斯虽然整体的准确度和布里尔分数不如多项式和高斯朴素贝叶斯和,但至少成功捕捉出了77.1%的少数类。可见,伯努利贝叶斯最能够忍受样本不均衡问题。
六、改进多项式朴素贝叶斯:补集朴素贝叶斯ComplementNB
补集朴素贝叶斯(complement naive Bayes,CNB)算法是标准多项式朴素贝叶斯算法的改进。
补集朴素贝叶斯牺牲了部分整体的精确度和布里尔指数,但是得到了十分高的召回率Recall,捕捉出了
98.7%的少数类,并且在此基础上维持了和原本的多项式朴素贝叶斯一致的AUC分数。和其他的贝叶斯算法比起来,
我们的补集朴素贝叶斯的运行速度也十分优秀。如果我们的目标是捕捉少数类,那我们毫无疑问会希望选择补集朴素
贝叶斯作为我们的算法。


3 、案例:贝叶斯分类器做文本分类
3.1 文本编码技术简介
3.1.1 单词计数向量(CountVectorizer类)
在开始分类之前,我们必须先将文本编码成数字。一种常用的方法是单词计数向量。在这种技术中,一个样本可以包含一段话或一篇文章,这个样本中如果出现了10个单词,就会有10个特征(n=10),每个特征 代表一个单词,特征的取值 表示这个单词在这个样本中总共出现了几次,是一个离散的,代表次数的,正整数。
在sklearn当中,单词计数向量计数可以通过feature_extraction.text模块中的CountVectorizer类实现,


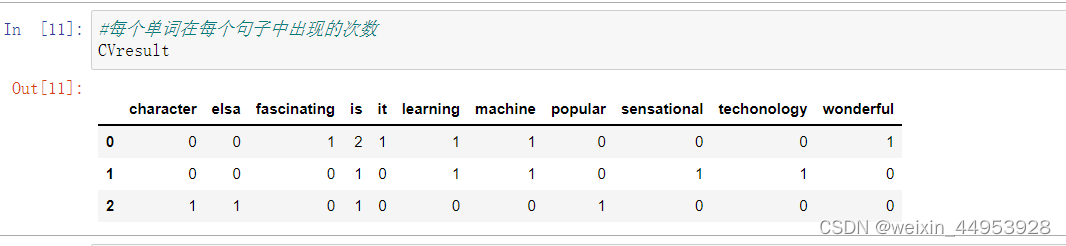
3.1.2 TF-IDF

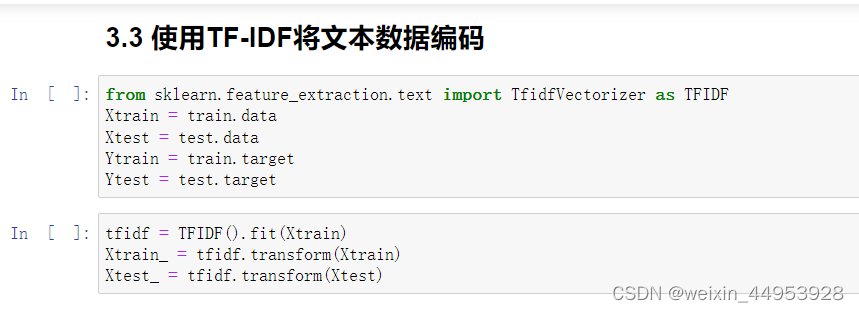
TF-IDF全称term frequency-inverse document frequency,词频逆文档频率,是通过单词在文档中出现的频率来衡量其权重,也就是说,IDF的大小与一个词的常见程度成反比,这个词越常见,编码后为它设置的权重会倾向于越小,以此来压制频繁出现的一些无意义的词。
在sklearn当中,我们使用feature_extraction.text中类TfidfVectorizer来执行这种编码。


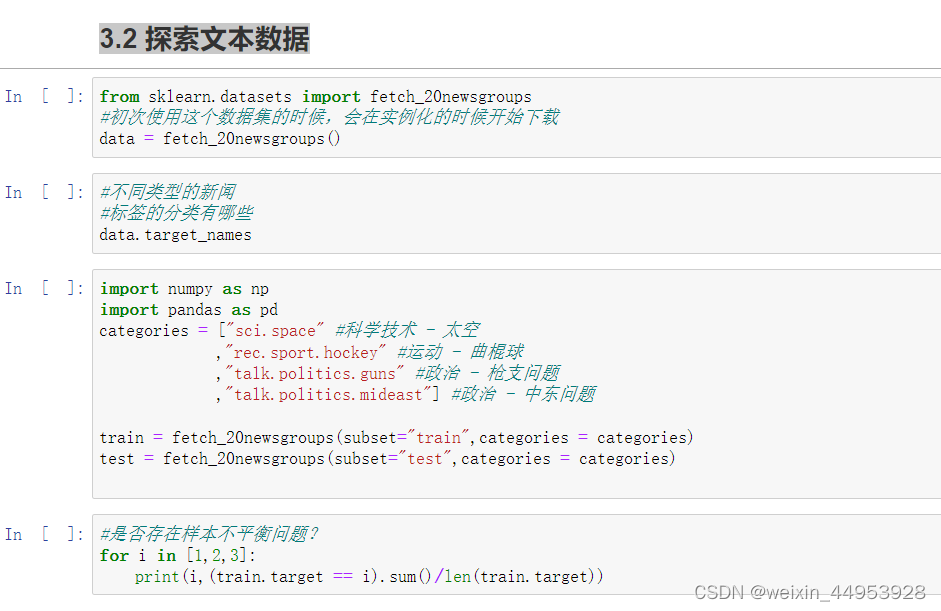
3.2 探索文本数据


详细说明
4.概率类模型的评估指标
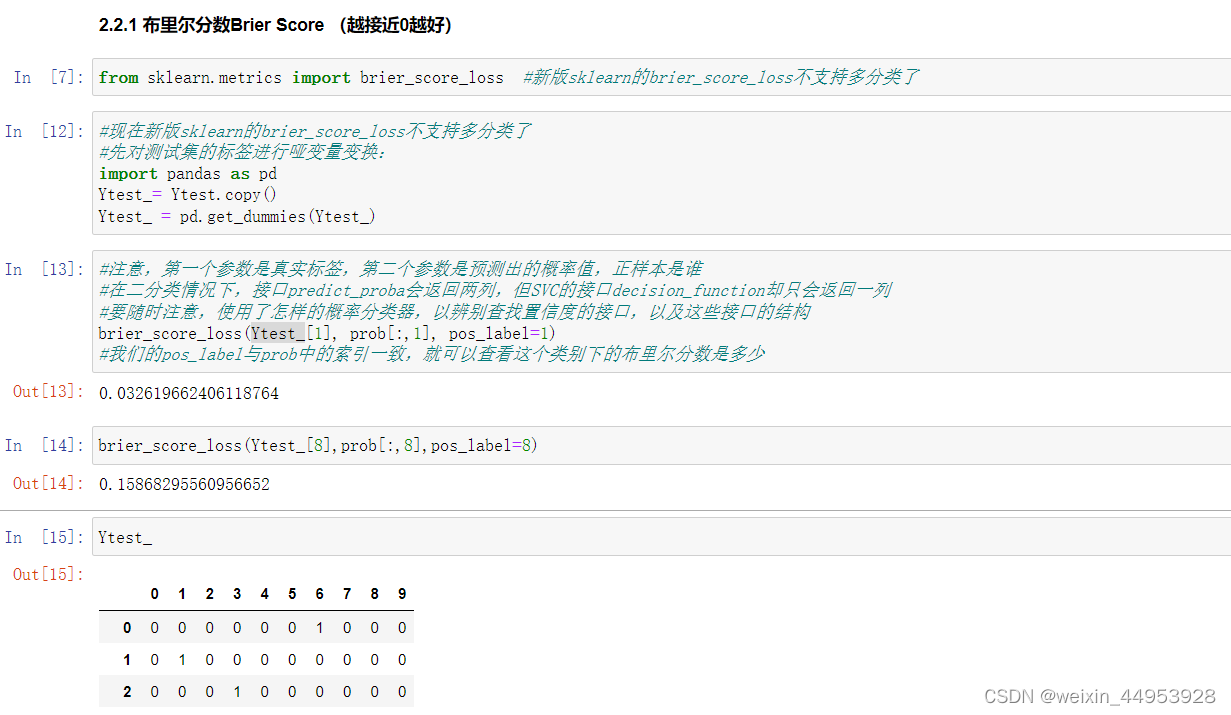
布里尔分数Brier Score