[人工智能]机器学习的相关知识-LDA、PCA

线性判别分析（LDA）

也是一种降维方法，思想就是

1. 多维空间中，数据处理分类问题较为复杂，LDA算法将多维空间中的数据投影到一条直线上，将$d$维数据转化成1维数据进行处理。
2. 对于训练数据，设法将多维数据投影到一条直线上，同类数据的投影点尽可能接近，异类数据点尽可能远离。
3. 对数据进行分类时，将其投影到同样的这条直线上，再根据投影点的位置来确定样本的类别。

“投影后类内方差最小，类间方差最大”

看这个图就明白了，在现实中$x$不止两维，但是思想一样的，就是每个点到这条直线上的投影，同类的接近，异类的远就好了。

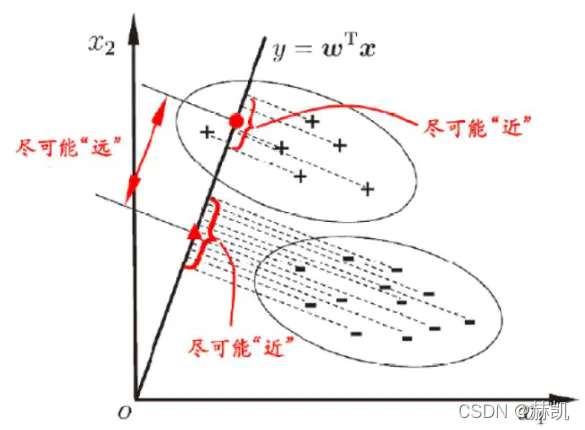
讲的真不错

主成分分析（PCA）

主要思想：

1. PCA就是将高维的数据通过线性变换投影到低维空间上去。
2. 投影思想：找出最能够代表原始数据的投影方法。被PCA降掉的那些维度只能是那些噪声或是冗余的数据。
3. 去冗余：去除可以被其他向量代表的线性相关向量，这部分信息量是多余的。
4. 去噪声，去除较小特征值对应的特征向量，特征值的大小反映了变换后在特征向量方向上变换的幅度，幅度越大，说明这个方向上的元素差异也越大，要保留。
5. 对角化矩阵，寻找极大线性无关组，保留较大的特征值，去除较小特征值，组成一个投影矩阵，对原始样本矩阵进行投影，得到降维后的新样本矩阵。
6. 完成PCA的关键是——协方差矩阵。协方差矩阵，能同时表现不同维度间的相关性以及各个维度上的方差。协方差矩阵度量的是维度与维度之间的关系，而非样本与样本之间。
7. 之所以对角化，因为对角化之后非对角上的元素都是0，达到去噪声的目的。对角化后的协方差矩阵，对角线上较小的新方差对应的就是那些该去掉的维度。所以我们只取那些含有较大能量(特征值)的维度，其余的就舍掉，即去冗余。

主要步骤如下：

1. 对所有的样本进行中心化，$x^{(i)}=x^{(i)}?\frac{1}{m}{\sum }_{j=1}^m{x}^{(j)}$ 。
2. 计算样本的协方差矩阵 $X{X}^T$ 。
3. 对协方差矩阵 $X{X}^T$ 进行特征值分解。
4. 取出最大的 $n^{\prime }$ 个特征值对应的特征向量 { w 1 , w 2 , . . . , w n ′ } \{ w_1,w_2,...,w_{n'} \} {w1?,w2?,...,wn′?} 。
5. 标准化特征向量，得到特征向量矩阵 $W$ 。
6. 转化样本集中的每个样本 $z^{(i)}=W^T{x}^{(i)}$ 。
7. 得到输出矩阵 $D^{\prime }=\left(z^{(1)},z^{(2)},...,z^{(n)}\right)?$ 。
   注：在降维时，有时不明确目标维数，而是指定降维到的主成分比重阈值 $k(k?(0,1])?$ 。假设 $n?$ 个特征值为 ${\lambda }_1?{\lambda }_2?...?{\lambda }_n?$ ，则 $n^{\prime }?$ 可从 ${\sum }_{i=1}^{n^{\prime }}{\lambda }_i?k\times {\sum }_{i=1}^n{\lambda }_i?$ 得到。

PCA

高维映射到低维，那就是映射出来的向量一定要分散，或者说是不同的高维向量映射下来应该是差异性尽可能的大。毕竟在高维就已经纠缠在一起了，低维还纠缠，那不就没意义了。
如何让映射在低维空间的向量更加分散呢？

• 映射出的低维向量要尽可能地差异化，就是说在低维度的空间里，要尽量保证原来高维度空间信息，所以在低维中向量的每个标量差异性要大，我理解就是代表的特征要完全不一样才好。（方差要大）
• 映射出不同的低维向量也要尽可能地线性无关。（协方差为0）

方差

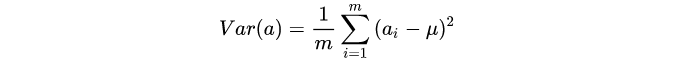
假如哈，每个变量的均值变化都为0，简化运算的。

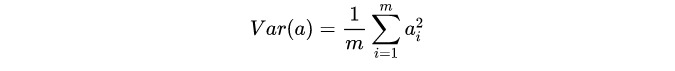
协方差

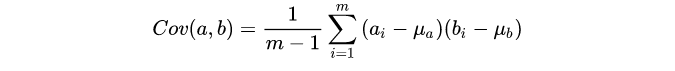
有时候$m$会很大，然后$m?1$用$m$代替。$u$是均值，一般定义为0，简化方程嘛。

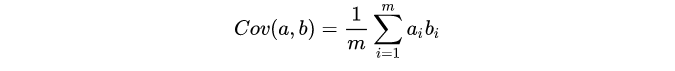
假如两个变量$a,b$，按行组成矩阵$X$:

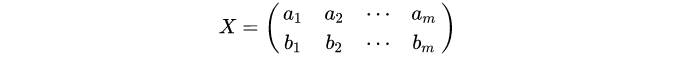
OK，自己个自己的转置乘一下，不就有了方差和协方差啦。

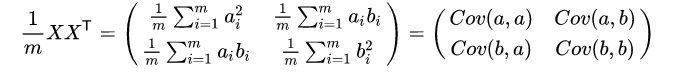
当然也可以不止两个向量，可以是特别多的向量。然后想起来，方差最大，协方差为0。那就是除了对角线，都为零，对角线？这不就是求矩阵的特征值莫，从大到小排列出来。

最终是将高维的$X$映射到低维空间，映射到话就是$Y=PX$，$P$就是一组正交基，假如$X$的协方差为$C$，$Y$的协方差为$D$。可以这么写：

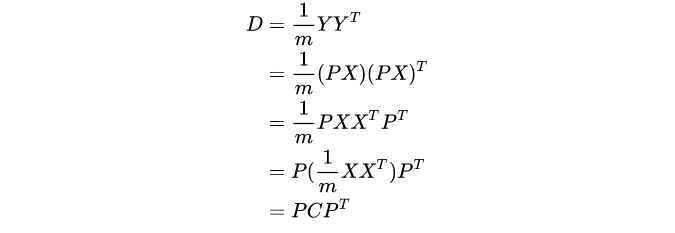
找到$P$帮助$C$完成对角化。协方差矩阵$C$就是一个对称矩阵，还是个实对称。实对称不同特征值的特征向量必须正交，不同的特征值对应的特征向量线性无关。

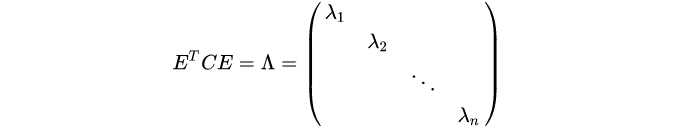
$P=E^T$，然后把特征值从大到小排列，取$P$的前$K$行组成矩阵，和原始矩阵做运算，就可以得到降维后的数据矩阵了。

有点类似图像里面的压缩，特征值越大所带的信息就越多，细节就可以忽略了。和SVD差不多奥。