[人工智能]基于MNIST数据集的CNN搭建与应用

提示：考研复试结束后，想具体学习一下CNN的搭建与应用，特意写下此篇文章来加深理解与应用，希望与csdn博客的同学一同学习与交流。

前言

随着深度学习的不断火爆，计算机视觉领域与自然语言处理出现了更多的创新需求，本文基于手写数字识别数据集MNIST，从零开始搭建卷积神经网络，一步一步在网络上搭建好之后进行训练集的训练，训练之后生成ckpt模型，后调用此模型进行测试。

一、CNN是什么？

1.个人自评与观点

目前处于大四阶段的我来讲，刚刚考完研，对于CNN有些许的陌生，之前大二的时候只是有所耳闻，但并未真正实践，现在从零开始学习卷积神经网络，虽然网上关于CNN（Convolutional Neural Network）的细致讲解，我的这篇文章只是为了强迫自己加深一下对CNN的理解与应用记忆，这篇文章可能有很多的漏洞，也希望有大佬看到我这篇菜鸡文章后，发现错误能够不吝文墨，能够指出我的错误，小菜鸡在此谢过了。

2.CNN拆分

（1）、输入层
输入层是整个卷积神经网络的入口，对于待处理的图像的卷积神经网络而言，这是一张图片的像素矩阵；
（2）、卷积层
传统的神经网络层之间均是全连接层，每一层的神经元与下一层的神经元依次相连，最终导致传统的网络需要的参数有“亿点点”多。。。

卷积层作为CNN中最重要的部分，这不得不提卷积核（过滤器）通常是33或者55大小，一个44的图片矩阵，经过一个33的卷积核，stride=1的情况下变为2*2的矩阵（不使用zero填充）；因此卷积层可以更加深入分析从而得到抽象度更高的特征。经过卷积层处理过的节点矩阵会变得更深，节点矩阵的深度会增加。
（3）、池化层
池化（pooling），又称为汇聚层，对于每个区域进行下采样，得到一个值，作为这个区域的概括；进行特征选择，降低特征数量，从而减少参数数量；
（4）、全连接层
经过多层的卷积与池化之后，最后从池化层出来的结果，一般会通过1~2个全连接层进行给出最后的分类结果，在特征提取完成之后，进行分类任务；
（5）、SoftMax层
主要用于进行分类，得到属于当前分类的比例概率大小。

3.CNN各层具体深入讲解

（1）、浅谈卷积神经网络
目前的卷积神经网络一般是由卷积层、汇聚层和全连接层交叉堆叠而成的前馈神经网络。同时，卷积神经网络有三个结构上的特性：局部连接、权重共享以及汇聚，这些特性使得卷积神经网络具有一定程度上的平移、缩放和旋转不变性，与普通的前馈神经网络相比，卷积神经网络的参数会更少。目前卷积神经网络，主要使用在图像和视频分析的各种任务，（比如图像分类、人脸识别、物体识别、图像分割等），准确率一般也比其他的神经网络模型要好。
（2）、何为卷积
卷积，也叫褶积，在图像处理中通常使用一维卷积或二维卷积；
通常，在图像处理过程中，因为图像作为一个二维结构，所以需要对一维卷积进行扩展，给定一个图像（input）与卷积核（滤波器），一般卷积核的大小远远小于图像的大小，输入信息input与滤波器的二维卷积定义为
Y=W*X
二维卷积实例图：

实例中给出的是，一个5X5的待卷积图像，卷积核大小为3X3，未采用零填充操作，故而得到的特征映射为3X3；
常用的高斯滤波器可以对图像进行平滑去噪；

卷积的主要功能，就是在一个图像上滑动一个卷积核（滤波器），通过卷积操作得到一组新的特征；在计算卷积的过程中，需要进行卷积核翻转，在具体视线中，以互相关操作来代替卷积，从而会减少一些不必要的操作或开销；
互相关与卷积的区别仅仅在于卷积核是否进行翻转，因此互相关也可以称为不翻转卷积；
（3）、卷积的变种
在卷积的标准定义基础上，引入卷积核的滑动步长（strides）、与零填充来增加卷积的多样性，可以更灵活的进行特征提取；
滑动步长是指：在卷积核在滑动时的时间间隔；
零填充（zero-Padding）是指：在输入向量两端进行补零操作
计算经过卷积之后的输出的空间尺寸公式：

（4）、卷积层的作用

1. 作用
   提取一个局部区域的特征，不同的卷积核相当于不同的特征提取器；

2. 具体说明
   由于卷积网络主要应用于在图像处理上，而图像作为二维结构，因此，为了更充分的利用图像的局部信息，通常将神经元组织为三维结构的神经层，其大小为，高度（W）*宽度（N）深度（D），由D个MN大小的特征映射构成。

3. 特征映射
   所谓的特征映射是指一幅图像在经过卷积提取到的特征，每个特征映射作为一类抽取的图像特征；为了提高卷积网络的表示能力，可以在每一层使用多个不同的特征映射，以更好地表示图像的特征。

4. 实例
   在输入层，特征映射就是图像本身，如果是灰度图像，就是有一个特征映射，输入层的深度为D=1,；如果是彩色图像，分别有RGB三个颜色通道的特征映射，输入层的深度D=3；

5. 结构
   输入特征映射组，为3维张量（Tensor）
   输出特征映射组，为3维张量（Tensor）
   卷积核，为4维张量（Tensor）

（5）、汇聚层的作用

1. 为何引入汇聚层
   卷积层虽然能够显著减少网络中的连接的数量，但特征映射组中的神经元个数并没有显著减少，如果后面接一个分类器，分类器的输入维数依然很高，很容易出现过拟合现象；为了解决这个问题，可以在卷积层之后加入一个汇聚层，从而降低特征维数，避免过拟合；

2. 何为汇聚层
   汇聚是指对每个区域进行下采样得到一个值，作为这个区域的概括。

3. 汇聚函数的种类
   最大汇聚：对于一个区域内，选择这个区域内所有神经元的最大活性值作为这个区域内的表示；
   平均汇聚：一般是取区域内所有神经元活性值的平均值。

4. 汇聚层的作用
   汇聚层不仅可以有效地减少神经元的数量，还可以使得网络对一些小的局部形态改变保持不变性，并拥有更大的感受野。

4.CNN的整体结构

（1）、卷积网络整体架构说明
一个典型的卷积网络由卷积层、汇聚层、全连接层交叉堆叠而成。目前常用的卷积网络架构如图：

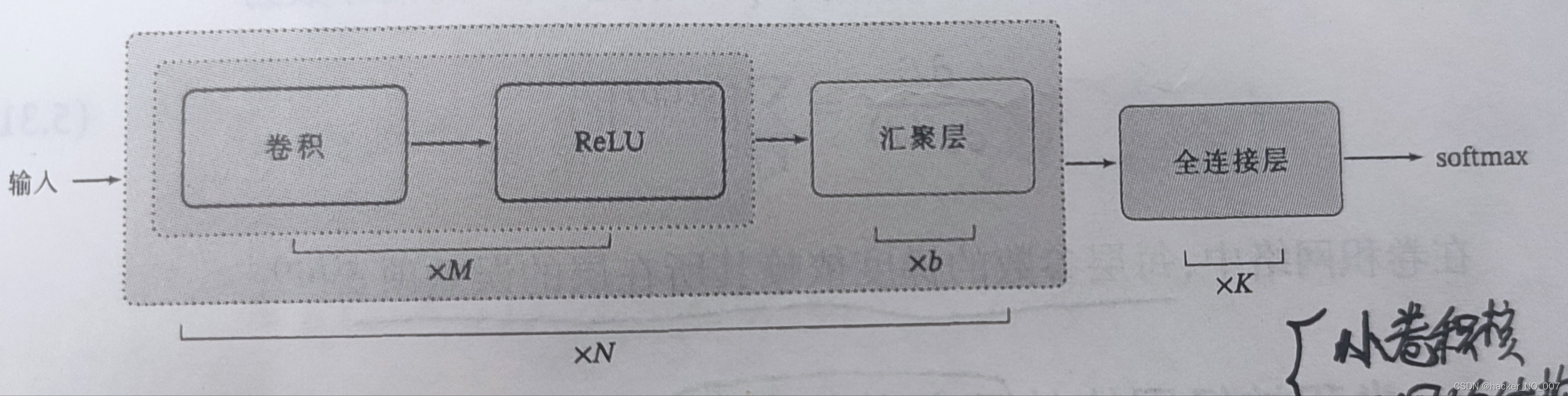
一个卷积块，为连续M个卷积层和b个汇聚层；
一个卷积网络中可以堆叠N个连续的卷积块，然后在后面接着K个全连接层；
目前，卷积网络的整体结构趋向于使用更小的卷积核，以及更深的结构，此外由于卷积的操作性越来越灵活，汇聚层的作用也变得越来越小，趋向于全卷积网络；

二、撸代码实战

1.利用TensorFlow，加载MNIST数据集

代码如下：

import tensorflow as tf
from tensorflow.examples.tutorials.mnist import input_data
import os

# 加载MNIST数据集，使用one_hot向量形式
mnist = input_data.read_data_sets('mnist_data', one_hot=True)

2.构造各个方法函数

（1）从截断的正太分布中输出随机值，从而生成随机参数和偏置值；

使用的tensorflow的封装函数：
tf.truncated_normal(shape,mean=0.0,stddev=1.0,dtype=tf.float32,seed=None,name=None)
参数说明：
shape：一维整数张量或 Python 数组，输出张量的形状。

mean：dtype 类型的 0-D 张量或 Python 值，截断正态分布的均值。

stddev：dtype 类型的 0-D 张量或 Python 值，截断前正态分布的标准偏差。

dtype：输出的类型。

seed：一个 Python 整数。用于为分发创建随机种子。查看tf.set_random_seed行为。

name：操作的名称（可选）。
函数返回值：返回指定形状的张量填充随机截断的正常值。
（2）调用生成参数值，与偏置值

# 初始化过滤器
def weight_variable(shape):
    # stddev一个python标量，要生成的随机值的标准偏差
    return tf.Variable(tf.truncated_normal(shape, stddev=0.1))


# 初始化偏置
def bias_variable(shape):
    return tf.Variable(tf.constant(0.1, shape=shape))

（3）调用TensorFlow的自带的卷积函数方法

tf.nn.conv2d(input, filter, strides, padding, use_cudnn_on_gpu=None, name=None)

除去name参数用以指定该操作的name，与方法有关的一共五个参数：

input：
指需要做卷积的输入图像，它要求是一个Tensor（张量），具有[batch, in_height, in_width, in_channels]这样的shape，具体含义是[训练时一个batch的图片数量, 图片高度, 图片宽度, 图像通道数]，注意这是一个4维的Tensor，要求类型为float32和float64其中之一；

filter：
相当于CNN中的卷积核，它要求是一个Tensor，具有[filter_height, filter_width, in_channels, out_channels]这样的shape，具体含义是[卷积核的高度，卷积核的宽度，图像通道数，卷积核个数]，要求类型与参数input相同，有一个地方需要注意，第三维in_channels，就是参数input的第四维；表示的是卷积层的权重，权重的类型必须与数据的类型一致。

strides：
卷积时在图像每一维的步长，这是一个一维的向量，长度4

padding： string类型的量，只能是”SAME”,”VALID”其中之一，这个值决定了不同的卷积方式，选项为"SAME"或"VALID",其中
"SAME"表示添加全零填充，保证卷积前输入的矩阵和卷积后的输出矩阵大小一致，
"VALID"表示不添加。

use_cudnn_on_gpu： bool类型，是否使用cudnn加速，默认为true

该函数的结果返回一个Tensor（张量），这个输出，就是我们常说的特征映射

# 卷积运算
def conv2d(x, w):
    # strides步长，
    return tf.nn.conv2d(x, w, strides=[1, 1, 1, 1], padding='SAME')

（4）TensorFlow的自带的池化层函数方法

tf.nn.max_pool(value, ksize, strides, padding, name=None)

参数是四个，和卷积很类似：

**value：**需要池化的输入，一般池化层接在卷积层后面，所以输入通常是特征映射，依然是[batch, height, width, channels]这样的shape

**ksize：**池化窗口的大小，取一个四维向量，一般是[1, height, width, 1]，因为我们不想在batch和channels上做池化，所以这两个维度设为了1

**strides：**和卷积类似，窗口在每一个维度上滑动的步长，一般也是[1, stride,stride, 1]

**padding：**和卷积类似，可以取’VALID’ 或者’SAME’

**函数结果：**返回一个Tensor，类型不变，shape仍然是[batch, height, width, channels]这种形式

# 池化计算
def max_pool_2x2(x):
    return tf.nn.max_pool(x, ksize=[1, 2, 2, 1], strides=[1, 2, 2, 1], padding='SAME')

（5）TensorFlow的自带的防止过拟合函数方法

tf.nn.dropout(x,keep_prob,noise_shape=None,seed=None, name=None)

**x：**指输入，输入的张量

keep_prob: float类型，每个元素被保留下来的概率，设置神经元被选中的概率,在初始化时keep_prob是一个占位符, keep_prob = tf.placeholder(tf.float32) 。tensorflow在run时设置keep_prob具体的值，例如keep_prob: 0.5

noise_shape : 一个1维的int32张量，代表了随机产生“保留/丢弃”标志的shape。

seed : 整形变量，随机数种子。

name：指定该操作的名字

dropout必须设置概率keep_prob，并且keep_prob也是一个占位符，跟输入是一样的
keep_prob = tf.placeholder(tf.float32)

**注意！！！**train的时候才是dropout起作用的时候，test的时候不应该让dropout起作用

# 防止过拟合进行dropout正则化
def dropout(input):
    # keep_prob为float类型，每个元素被保留下的概率，设置神经元被选中的概率，
    # keep——prob是一个占位符
    keep_prob = tf.placeholder(tf.float32)
    return keep_prob, tf.nn.dropout(input, keep_prob)

（6）TensorFlow的激活函数

tf.nn.relu(features, name = None)

作用：

计算激活函数 relu，即 max(features, 0)。即将矩阵中每行的非最大值置0。是将大于0的数保持不变，小于0的数置为0，计算修正线性单元(非常常用)：max(features, 0).并且返回和feature一样的形状的tensor。

参数：

features: tensor类型，必须是这些类型：A Tensor. float32, float64, int32, int64, uint8, int16, int8, uint16, half.

name: ：操作名称（可选）

（7）重塑张量reshape函数

reshape( tensor, shape, name=None )

tensor：一个Tensor；

shape：一个Tensor；必须是以下类型之一：int32，int64；用于定义输出张量的形状。

**name：**操作的名称（可选）。

返回值：该操作返回一个Tensor。与tensor具有相同的类型。

（8）矩阵向量相乘

tf.matmul(a, b, transpose_a=False, transpose_b=False, adjoint_a=False, adjoint_b=False, a_is_sparse=False, b_is_sparse=False, name=None)

参数:

a: 一个类型为 float16, float32, float64, int32, complex64, complex128 且张量秩 > 1 的张量。

b: 一个类型跟张量a相同的张量。

transpose_a: 如果为真, a则在进行乘法计算前进行转置。

transpose_b: 如果为真, b则在进行乘法计算前进行转置。

adjoint_a: 如果为真, a则在进行乘法计算前进行共轭和转置。

adjoint_b: 如果为真, b则在进行乘法计算前进行共轭和转置。

a_is_sparse: 如果为真, a会被处理为稀疏矩阵。

b_is_sparse: 如果为真, b会被处理为稀疏矩阵。

name: 操作的名字（可选参数）

返回值：一个跟张量a和张量b类型一样的张量且最内部矩阵是a和b中的相应矩阵的乘积。

注意：

（1）输入必须是矩阵（或者是张量秩 >２的张量，表示成批的矩阵），并且其在转置之后有相匹配的矩阵尺寸。

（2）两个矩阵必须都是同样的类型，支持的类型如下：float16, float32, float64, int32, complex64, complex128。

# 分类用，softmax输出
def softmax(input, weight_shape, bias_shape):
    """
    :param input: 从全连接层输入的张量
    :param weight_shape:
    :param bias_shape:
    :return: 最后经过softmax函数，将输出转化为概率的问题
    """
    w = weight_variable(weight_shape)
    b = bias_variable(bias_shape)
    return tf.nn.softmax(tf.matmul(input, w) + b)

（9）定义损失函数和优化器

# 定义损失函数和优化器
def optimizer(label, y):
    loss = tf.reduce_mean(-tf.reduce_sum(label * tf.log(y)))
    return tf.train.AdamOptimizer(1e-4).minimize(loss), loss

计算张量的各个维度上的元素的平均值

reduce_mean(input_tensor, axis=None, keep_dims=False,name=None,reduction_indices=None )

参数：

**input_tensor：**要减少的张量。应该有数字类型。
**axis：**要减小的尺寸。如果为None（默认），则减少所有维度。必须在[-rank(input_tensor), rank(input_tensor))范围内。
keep_dims：如果为true，则保留长度为1的缩小尺寸。

**name：**操作的名称（可选）。
reduction_indices：axis的不支持使用的名称。

**函数返回值：**该函数返回减少的张量。numpy兼容性相当于np.mean

3.调用各个方法函数

（1）构建卷积块

# 卷积层
def conv_layer(input, filter_shape, bias_shape):
    """

    :param input: 需要做卷积的输入图像，是一个张量，4维tensor，类型为float32
    :param filter_shape: 过滤器的大小，相当于卷积核，张量,4维
    :param bias_shape: 偏置值的大小
    :return: 卷积之后进行池化操作
    """
    w = weight_variable(filter_shape)
    b = bias_variable(bias_shape)
    # 使用conv2d函数进行卷积运算，然后在用ReLu作为激活函数
    h = tf.nn.relu(conv2d(input, w) + b)
    # 卷积以后再经过池化操作
    return max_pool_2x2(h)

（2）构建全连接层

# 定义全连接层的方法函数
def dense(input, weight_shape, bias_shape, reshape):
    """
    :param input: 接受从卷积池化之后的数据
    :param weight_shape: 权重
    :param bias_shape: 偏置值
    :param reshape:
    :return:经过卷积层以后，我们得到的数据是一个矩阵形式
    """
    w = weight_variable(weight_shape)
    b = bias_variable(bias_shape)
    h = tf.reshape(input, reshape)
    # 使用ReLu作为激活函数
    return tf.nn.relu(tf.matmul(h, w) + b)

（3）构建softmax做分类

# 分类用，softmax输出
def softmax(input, weight_shape, bias_shape):
    """
    :param input: 从全连接层输入的张量
    :param weight_shape:
    :param bias_shape:
    :return: 最后经过softmax函数，将输出转化为概率的问题
    """
    w = weight_variable(weight_shape)
    b = bias_variable(bias_shape)
    return tf.nn.softmax(tf.matmul(input, w) + b)

（4）计算模型预测准确率

# 计算模型预测准确率
def accuracy(label, y):
    pred = tf.equal(tf.argmax(y, 1), tf.argmax(label, 1))
    return tf.reduce_mean(tf.cast(pred, tf.float32))

对比这两个矩阵或者向量的相等的元素

tf.equal(A, B)

如果是相等的那就返回True，反正返回False，返回的值的矩阵维度和A是一样的

例如：
A = [[1,3,4,5,6]]
B = [[1,3,4,3,2]]
with tf.Session() as sess:
print(sess.run(tf.equal(A, B)))
[[ True True True False False]]
该函数将返回一个 bool 类型的张量。

（5）搭建网络结构

# 搭建网络结构
def net(input, label):
    """
    第一层卷积，将过滤器设置成5*5*1的矩阵
    5*5表示过滤器的大小，1表示深度，mnist的图片为黑白图片，只有一层
    32表示，要有32个卷积核，最终得到32个特征图
    :param input:
    :param label:
    :return:
    """

    c1 = conv_layer(input, [5, 5, 1, 32], [32])
    # 第二层卷积，经过第一层卷积加池化
    c2 = conv_layer(c1, [5, 5, 32, 64], [64])

    # 全连接层
    f1 = dense(c2, [7 * 7 * 64, 1024], [1024], [-1, 7 * 7 * 64])

    # 防止过拟合
    keep_prob, h = dropout(f1)

    # softmax最后输出
    y = softmax(h, [1024, 10], [10])

    # 定义损失函数和优化器
    op, loss = optimizer(label, y)

    # 计算预测准确率
    acc = accuracy(label, y)
    return acc, op, keep_prob, loss

4.训练结果与预测

总结

写了一天的博客，累了，就写到这吧，我把最后的完整代码我上传，把链接放在评论区；