[人工智能]实现3层神经网络

实现简单的三层神经网络

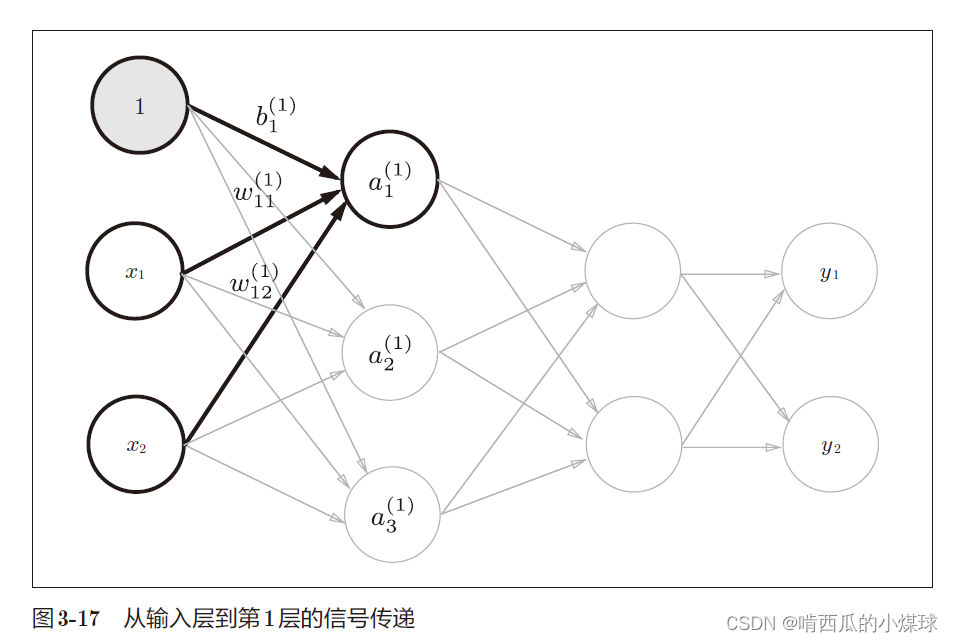
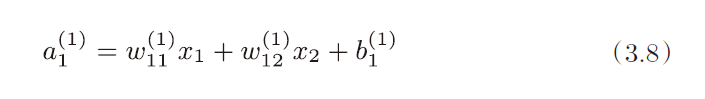
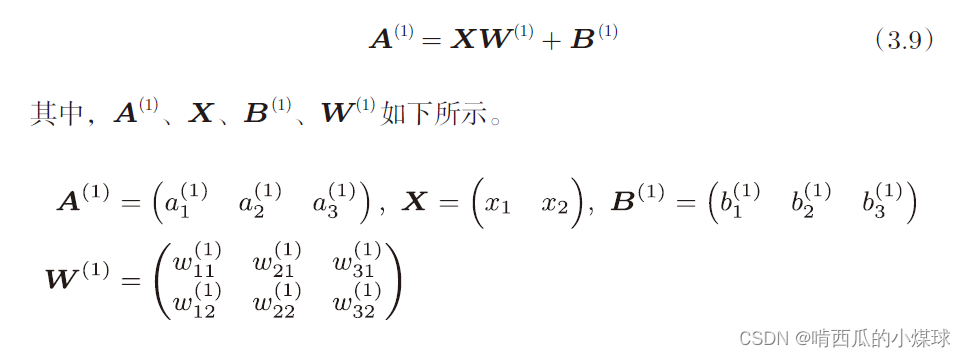
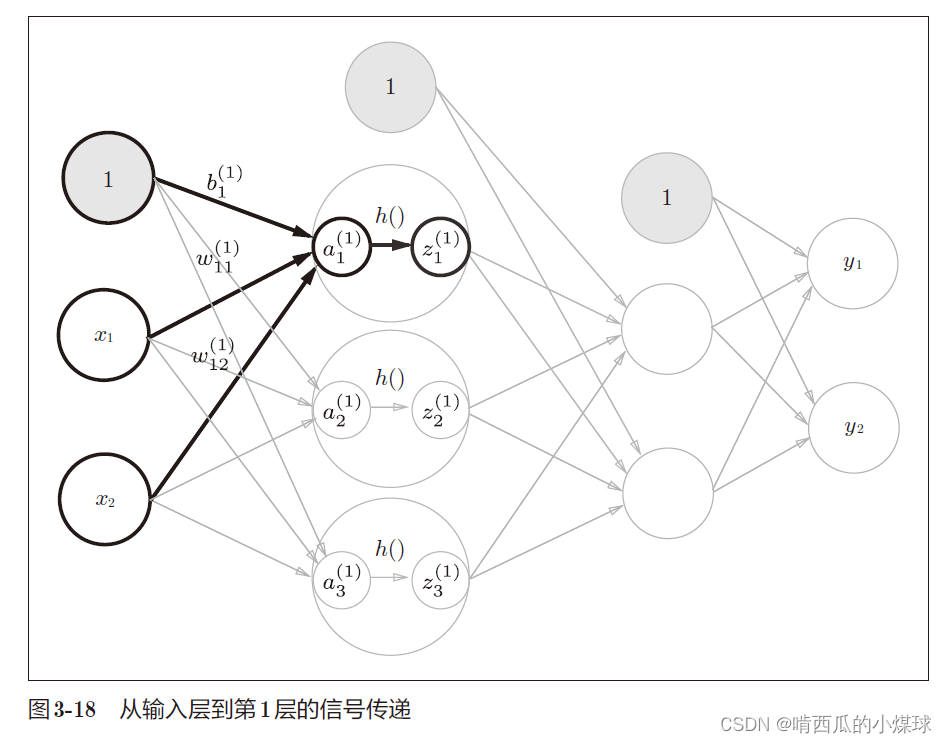
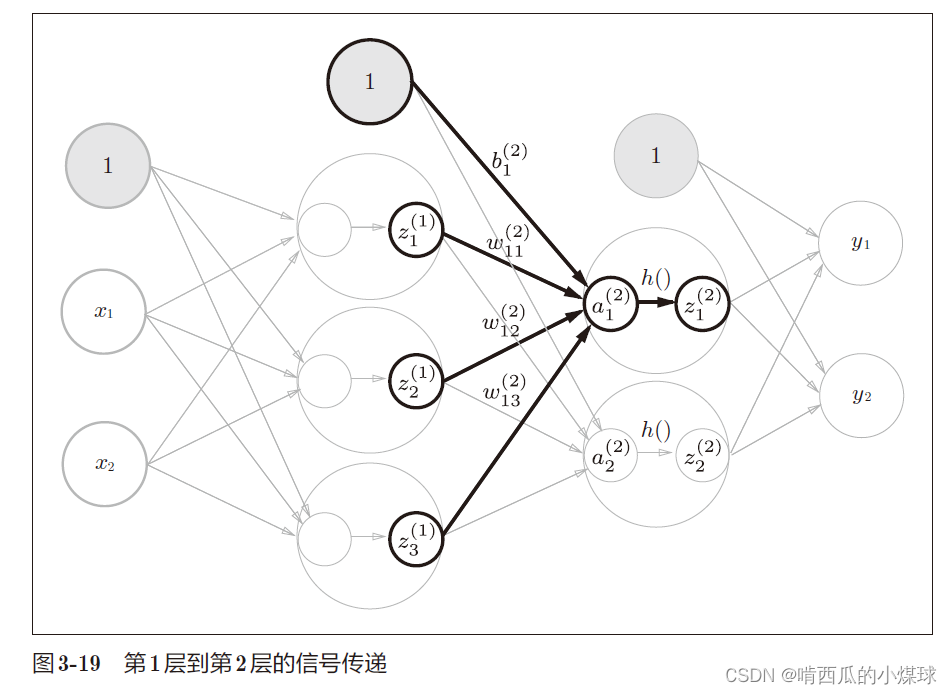
在第2层到输出层用的激活函数和之前的隐藏层有所不同，之前的隐藏层使用的是sigmoid函数，我们定义了identity_function()函数（也称为“恒等函数”），并将其作为输出层的激活函数。恒等函数会将输入原样输出。此外输出层的激活函数用σ() 表示，不同于隐藏层的激活函数h(x)。

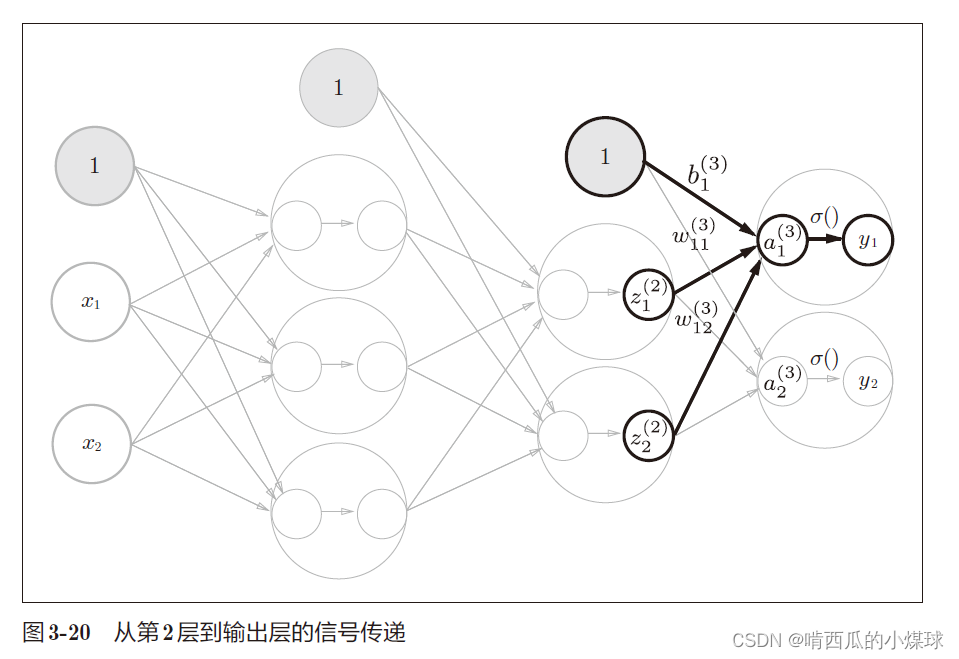
对于输出层所用的激活函数，回归问题可以用恒等函数，二元分类问题可以使用sigmoid函数，多元分类问题可以使用softmax函数。
何为回归问题？
回归问题是根据某个输入预测一个（连续的）数值的问题。比如，根据一个人的图像预测这个人的体重的问题就是回归问题。

# 教材p63 手动实现3层的神经网络
import numpy as np
# 从sigmoid.py文件中导入sigmoid函数
from sigmoid import sigmoid


def identity_function(x):
    return x


# init_network()函数用于对每一层权重和偏置进行初始化，并将它们保存在字典变量network中
def init_network():
    network = {}
    network['W1'] = np.array([[0.1, 0.3, 0.5], [0.2, 0.4, 0.6]])
    network['b1'] = np.array([0.1, 0.2, 0.3])
    network['W2'] = np.array([[0.1, 0.4], [0.2, 0.5], [0.3, 0.6]])
    network['b2'] = np.array([0.1, 0.2])
    network['W3'] = np.array([[0.1, 0.3], [0.2, 0.4]])
    network['b3'] = np.array([0.1, 0.2])
    return network


# forward()函数用于封装将输入信号转换为输出信号的处理过程
def forward(network, x):
    W1, W2, W3 = network['W1'], network['W2'], network['W3']
    b1, b2, b3 = network['b1'], network['b2'], network['b3']

    a1 = np.dot(x, W1) + b1
    z1 = sigmoid(a1)
    a2 = np.dot(z1, W2) + b2
    z2 = sigmoid(a2)
    a3 = np.dot(z2, W3) + b3
    y = identity_function(a3)

    return y


network = init_network()
x = np.array([1.0, 0.5])
y = forward(network, x)
print(y)

恒等函数和softmax函数

恒等函数会将输入按照原样输出，上面的代码中使用的就是恒等函数。
softmax函数公式如下

为了解决溢出问题，可以对（3.10）做出以下改进

def softmax(a):
	c = np.max(a)
	exp_a = np.exp(a - c) # 溢出对策
	sum_exp_a = np.sum(exp_a)
	y = exp_a / sum_exp_a
	return y