思路
sigmoid函数做激活函数
二分类交叉熵做损失函数
mian函数:数据预处理
split函数:数据集分割
training函数:神经网络训练
testing函数:神经网络测试
留言
1、这虽是单隐层神经网络,但是这分类效果好得出奇,好不容易才训练出86.7%这么低的准确率(接受误差:[-0.02 0.02]),可能是因为数据集太好了,或者数据集太小了,训练出来一般都是100%的准确率
2、由于用的是二分类交叉熵做损失函数,于是将类别编号为0、1的保留,其他的剔除,可修改损失函数做所有鸢尾花数据集的分类
3、数据集下载
修正数据集下载地址,提取码:5c02
原数据集,提取码:got0
效果
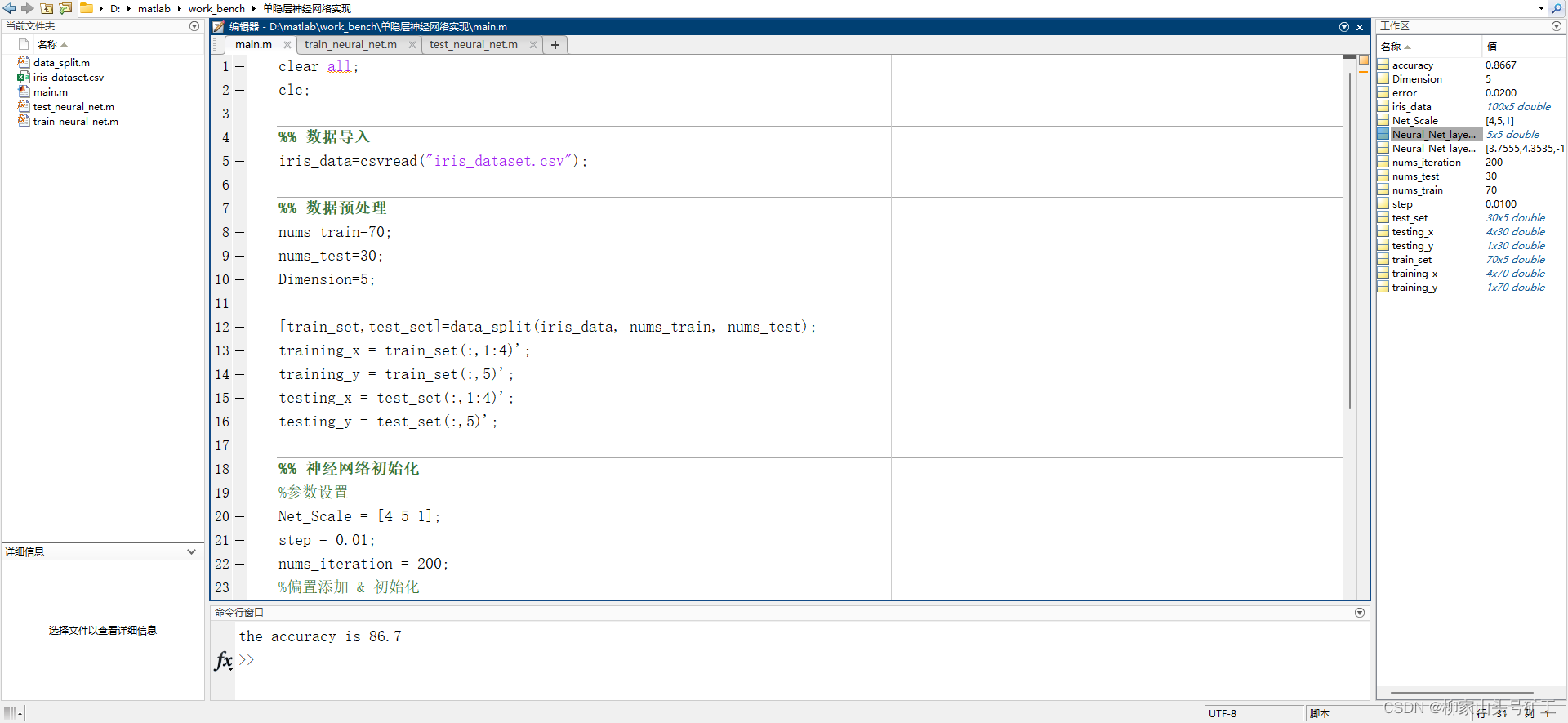
代码
mian
clear all;
clc;
%% 数据导入
iris_data=csvread("iris_dataset.csv");
%% 数据预处理
nums_train=70;
nums_test=30;
Dimension=5;
[train_set,test_set]=data_split(iris_data, nums_train, nums_test);
training_x = train_set(:,1:4)';
training_y = train_set(:,5)';
testing_x = test_set(:,1:4)';
testing_y = test_set(:,5)';
%% 神经网络初始化
%参数设置
Net_Scale = [4 5 1];
step = 0.01;
nums_iteration = 200;
%偏置添加 & 初始化
global Neural_Net_layer_1;
global Neural_Net_layer_2;
Neural_Net_layer_1 = rand([Net_Scale(2) Net_Scale(1)]+[0 1]);
Neural_Net_layer_2 = rand([Net_Scale(3) Net_Scale(2)]+[0 1]);
%% 神经网络训练
train_neural_net(training_x,training_y,step, nums_iteration);
%% 神经网络评价
error = 0.02;
accuracy = test_neural_net(testing_x,testing_y,error);
fprintf("the accuracy is %.1f\n%",100*accuracy);
split
function [training,testing] = data_split(data,nums_train,nums_test)
training=data(1:nums_train,:);
testing=data(1:nums_test,:);
end
training
function []= train_neural_net(training_x,training_y,step,nums_iteration)
%接收每层神经网络层参数, 训练数据
%返回每层神经网络参数
global Neural_Net_layer_1;
global Neural_Net_layer_2;
%每层参数规模
size_layer_1=size(Neural_Net_layer_1);
size_layer_2=size(Neural_Net_layer_2);
for i = 1: nums_iteration
%输出层计算 arrayfun函数:激活函数(Sigmoid)作用于矩阵内每个数值
%第一层
W_X_1 = Neural_Net_layer_1(:,1: size_layer_1(2)-1) * training_x;
W_X_B_1 = W_X_1+ Neural_Net_layer_1(:,size_layer_1(2));
layer_1 = arrayfun(@(x) 1/(1+exp(-x)), W_X_B_1);
%第二层
W_X_2 = Neural_Net_layer_2(:,1: size_layer_2(2)-1) * layer_1;
W_X_B_2 = W_X_2+ Neural_Net_layer_2(:,size_layer_2(2));
layer_2 = arrayfun(@(x) 1/(1+exp(-x)), W_X_B_2);
%损失函数误差计算
%第三层
a_grad_3 = arrayfun(@(x,y) (1-y)./(1-x)-(y./x),layer_2,training_y);
%第二层
a_grad_2 = Neural_Net_layer_2(:,1: size_layer_2(2)-1)'*a_grad_3;
%激活函数自变量梯度计算
%第三层
z_grad_3 = a_grad_3.*layer_2.*(1-layer_2);
%第二层
z_grad_2 = a_grad_2.*layer_1.*(1-layer_1);
%梯度下降
%W的梯度下降
Neural_Net_layer_2(:,1: size_layer_2(2)-1) = Neural_Net_layer_2(:,1: size_layer_2(2)-1) - step.*z_grad_3*layer_1';
Neural_Net_layer_1(:,1: size_layer_1(2)-1) = Neural_Net_layer_1(:,1: size_layer_1(2)-1) - step.*z_grad_2*training_x';
%b的梯度下降
Neural_Net_layer_2(:,size_layer_2(2)) = Neural_Net_layer_2(:,size_layer_2(2)) - sum(step*z_grad_3,2);
Neural_Net_layer_1(:,size_layer_1(2)) = Neural_Net_layer_1(:,size_layer_1(2)) - sum(step*z_grad_2,2);
end
end
testing
function [accuracy] = test_neural_net(testing_x,testing_y,error)
global Neural_Net_layer_1;
global Neural_Net_layer_2;
%测试集规模
size_test=size(testing_x);
%每层参数规模
size_layer_1=size(Neural_Net_layer_1);
size_layer_2=size(Neural_Net_layer_2);
%输出层计算
%第一层
W_X_1 = Neural_Net_layer_1(:,1: size_layer_1(2)-1) * testing_x;
W_X_B_1 = W_X_1+ Neural_Net_layer_1(:,size_layer_1(2));
layer_1 = arrayfun(@(x) 1/(1+exp(-x)), W_X_B_1);
%第二层
W_X_2 = Neural_Net_layer_2(:,1: size_layer_2(2)-1) * layer_1;
W_X_B_2 = W_X_2+ Neural_Net_layer_2(:,size_layer_2(2));
layer_2 = arrayfun(@(x) 1/(1+exp(-x)), W_X_B_2);
%正确率计算
accuracy = sum(abs(layer_2-testing_y)<=error)/size_test(2);
end