[人工智能]PointNet++论文和代码阅读

PointNet++: Deep Hierarchical Feature Learning on Point Sets in a Metric Space

Charles R. Qi Li Yi Hao Su Leonidas J. Guibas
Stanford University

Abstract

Few prior works study deep learning on point sets. PointNet is a pioneer in this direction. However, by design PointNet does not capture local structures induced by the metric space points live in, limiting its ability to recognize fine-grained patterns and generalizability to complex scenes. In this work, we introduce a hierarchical neural network that applies PointNet recursively on a nested partitioning of the input point set. By exploiting metric space distances, our network is able to learn local features with increasing contextual scales. With further observation that point sets are usually sampled with varying densities, which results in greatly decreased performance for networks trained on uniform densities, we propose novel set learning layers to adaptively combine features from multiple scales. Experiments show that our network called PointNet++ is able to learn deep point set features efficiently and robustly. In particular, results significantly better than state-of-the-art have been obtained on challenging benchmarks of 3D point clouds.

引言

PointNet的问题

? PointNet不捕获局部结构，然而，利用局部结构已被证明是卷积结构成功的重要因素。CNN将规则网格上定义的数据作为输入，并能够沿着多分辨率层级结构逐步捕获越来越大的尺度上的特征。在较低层级时，神经元的感受野较小，而在较高层级时，神经元的感受野较大。沿着层级抽象局部模式的能力允许对不可见的情况有更好的泛化能力。

PointNet++

? PointNet++以层级的方式处理度量空间中采样的一组点。

? PointNet++的总体思想很简单。首先根据underlying space的距离度量将集合中的点划分为重叠的局部区域。与CNN相似，PointNet++提取局部特征，从小的邻域捕获精细的几何结构；这些局部特征被进一步分组成更大的单元，并被处理以产生更高层次的特征。这个过程不断重复，直到得到整个点集的特征。

? PointNet++需要解决两个问题：

• 如何得到点集的划分；

• 如何通过局部特征学习器抽象点集或局部特征集；

  这两个问题是相关的，因为对点集的划分必须产生横跨划分的通用结构，以便共享局部特征学习器的权值，就像卷积那样。PointNet++将PointNet作为局部学习器，因为PointNet对无序的点集具有很好的语义特征抽取能力。作为一个基本的构建块，PointNet将局部点或特征集抽象为更高级别的表示。从这个角度看，PointNet++递归地对输入集的嵌套划分应用PointNet。

最远点采样算法

? 如何生成点集的重叠划分？每个划分(partition)定义为欧氏空间中的邻域球(neighborhood ball)，其参数包括质心位置和尺度。为了均匀地覆盖整个集合，通过**最远点采样算法（FPS）**在输入点集合中选择质心。与用固定stride扫描空间的volumetric CNN相比，这里的局部感受野依赖于输入数据和度量，因此更高效和有效。

局部尺度的确定

? 然而，由于特征尺度的纠缠性和输入点集的非均匀性，局部邻域球的合适尺度的确定是一个更难的问题。这里假设输入点集在不同区域的密度是可变的，这在实际数据中是很常见的(见图1)。

? 由此可见，PointNet++输入点集与CNN输入非常不同，CNN输入可以被视为定义在均匀恒定密度的规则网格上的数据。在CNN中，与局部划分尺度相对应的是kernel的大小。且使用较小的卷积核有助于提高CNN的能力。然而，在点云数据上确相反，由于抽样不足，小的邻域可能由太少的点组成，这可能不足以让PointNet鲁棒地捕获模式。

? PointNet++在多个尺度上利用邻域来实现鲁棒性和细节捕获。在训练过程中辅助随机的输入dropout，网络自适应学习不同尺度检测到的权值模式，并根据输入数据结合多尺度特征。

问题定义

? 假设 $\mathcal{X}=(M,d)$ 是一个离散度量空间，它的度量继承自欧氏空间 ${\mathbb{R}}^n$ ，其中 $M?{\mathbb{R}}^n$ 是点的集合，d是距离距离。M的密度可能是不均匀的。我们的目标是是学习集合函数 $f$ ，它以 $\mathcal{X}$ 作为输入(以及每个点的附加特征)，并产生语义兴趣重新分级 $\mathcal{X}$ 的信息。实际上，这样的 $f$ 可以是给 $\mathcal{X}$ 分配一个标签的分类函数，也可以是给M中的每个成员分配一个点标签的分割函数。

方法

回顾PointNet

? PointNet是一个通用连续集合函数逼近器。给定一个无序点集合 { x 1 , x 2 , ? ? , x n } , x i ∈ R d \{ x_1,x_2,\cdots, x_n \}, x_i \in \mathbb{R}^d {x1?,x2?,?,xn?},xi?∈Rd ，定义一个映射点集到向量的集合函数 $f:\mathcal{X}\to \mathbb{R}$ ：

f ( x 1 , x 2 , ? ? , x n ) = γ ( max ? i = 1 , ? ? , n { h ( x i ) } ) (1) f ( x_1,x_2,\cdots,x_n ) = \gamma \left( \max \limits_{i=1,\cdots,n} \{ h(x_i) \} \right) \tag{1} f(x1?,x2?,?,xn?)=γ(i=1,?,nmax?{h(xi?)})(1)
? 其中 $\gamma$ 和 $h$ 使用MLP网络。

? 式(1)中的集合函数 $f$ 不受输入点云排列的影响，可以任意逼近任意连续的集合函数。 $h$ 的响应可以解释为一个点的空间编码。

? PointNet在一些基准测试上取得了令人印象深刻的效果。然而，它缺乏在不同尺度上捕捉局部上下文的能力。

层级点集特征学习

? PointNet使用单个max pooling运算来聚合整个点集，而PointNet++构建一个层次化的点分组，并沿着层次结构逐步抽象越来越大的局部区域。

? PointNet++层次结构是由许多集合抽象层(set abstraction levels)组成的(图2)。

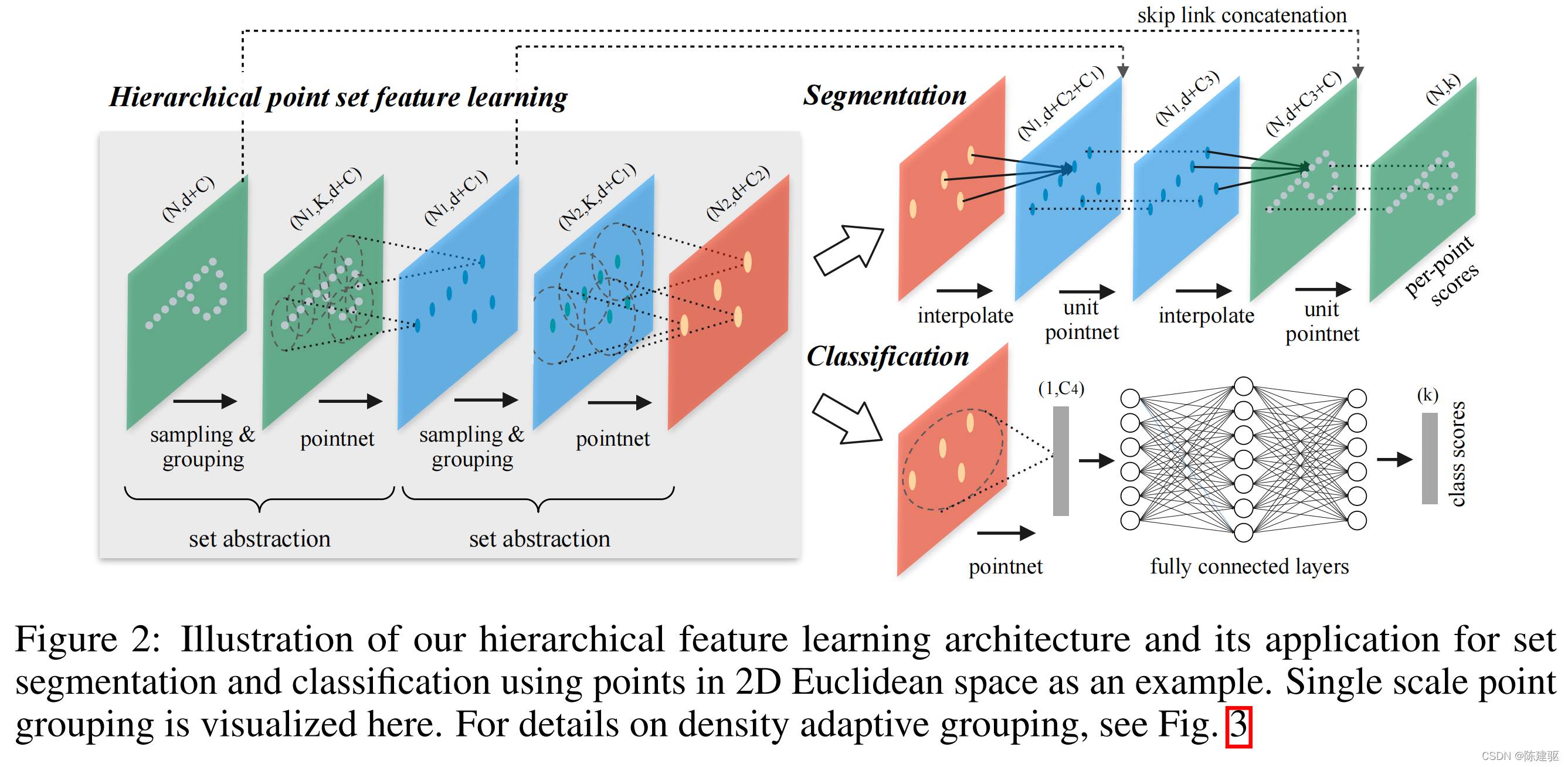
? 在每个层级上，一组点被处理和抽象，以产生一个包含较少元素的新集合。set abstraction层由三个关键层组成:Sampling层、Grouping层和PointNet层。

• Sampling层从输入点云中选择一组点，这些点定义了局部区域的质心。

• Grouping层通过寻找质心周围的相邻点来构造局部区域集合。

• PointNet层使用一个mini-PointNet将局部区域模式编码为特征向量。

  set abstraction层输入是N个点的C维向量，每个点的坐标是一个d维向量，所以输入矩阵的维度为 $N\times (d+C)$ 。输出的维度是 $N^{\prime }\times (d+C^{\prime })$ ，即N’个采样点，每个采样点从局部上下文中生成C’维的向量。

Sampling层

? 输入：点集 { x 1 , x 2 , ? ? , x n } \{ x_1,x_2,\cdots,x_n \} {x1?,x2?,?,xn?} 。使用最远点采样（FPS）选择一个点的子集 { x i 1 , x i 2 , ? ? , x i m } \{ x_{i_1},x_{i_2},\cdots,x_{i_m} \} {xi1??,xi2??,?,xim??} ，使 $x_{i_j}$ 是相对于其余点集 { x i 1 , x i 2 , ? ? , x i j ? 1 } \{ x_{i_1},x_{i_2},\cdots,x_{i_{j-1}} \} {xi1??,xi2??,?,xij?1??} 的最远点 (以度量距离)。

? 与随机采样相比，在质心数目相同的情况下，该方法对整个点集具有更好的覆盖效果。相比之下，CNN扫描向量空间而不关心数据分布，FPS以数据依赖的方式生成感受野。

Grouping层

? 输入：一组大小为 $N\times (d+C)$ 的点集，一组大小为 $N^{\prime }\times d$ 的质心坐标。输出为大小 $N^{\prime }\times K\times (d+C)$ 的点集组，每一组对应于一个局部区域，包括 K 个邻域点。

? 注意，K 随组而变化，但后面的PointNet层能够将不同数量的点集转换为固定长度的局部区域特征向量。

? 在卷积神经网络中，像素的局部区域由像素在一定的曼哈顿距离(卷积核大小)内具有数组索引的像素组成。而在采样的点集中，点的邻域由度量距离定义。

? 使用Ball query查找到质心点半径范围内的所有点(在实现中会设置K的上限)。另一种范围查询的方式是K近邻(kNN)搜索，它找到固定数量的相邻点。与kNN相比，Ball query的局部邻域保证了固定的区域尺度，使得局部区域特征在空间上更具有泛化性，在需要局部模式识别的任务(如语义点标注)中更常见。

PointNet层

? 输入：N’ 个点云的局部区域，大小为 $N^{\prime }\times K\times (d+C)$ 。每个局部区域由质心和其邻域进行编码的局部特征抽象出来。

? 输出：大小为 $N^{\prime }\times (d+C^{\prime })$

? 首先将局部区域中点的坐标平移到相对于质心点的局部坐标系，设 $\hat{x}$ 是质心的坐标：
$$x_i^{(j)}=x_i^{(j)}?{\hat{x}}^{(j)},i=1,2,?,K,j=1,2,?,d$$
? 使用PointNet作为基本的构建块来学习局部模式。通过使用相对坐标和点特征，我们可以在局部区域捕获点对点的关系。

非均匀采样密度下的鲁棒特征学习

PointNet++

? 点集在不同区域的密度不均匀是很常见的现象。这种非均匀性给点集特征学习带来问题。在密集数据中学习到的特征可能不能推广到稀疏采样的区域。因此，为稀疏点云训练的模型可能无法识别细粒度的局部结构。

? 理想情况下，我们希望尽可能近距离地查看一个点集，以捕捉密集采样区域的最佳细节。然而，这种近距离的查看在低密度区域是不可行的，因为采样的缺陷可能会破坏局部模式。在这种情况下，我们应该在更大的邻域内寻找更大尺度的模式。

? 为了实现这一目标，我们提出了密度自适应PointNet层(图3)，当输入采样密度发生变化时，该层可以学习结合来自不同尺度区域的特征。

? 称这种带密度自适应PointNet层的层级网络为PointNet++。

? 前面介绍，每个抽象层都包含单尺度的grouping和特征提取。在PointNet++中，每个抽象层提取多尺度的局部模式，并根据局部点密度对它们进行智能组合。在grouping局部区域和结合不同尺度特征时，本文提出了两种密度自适应层，如下所示。

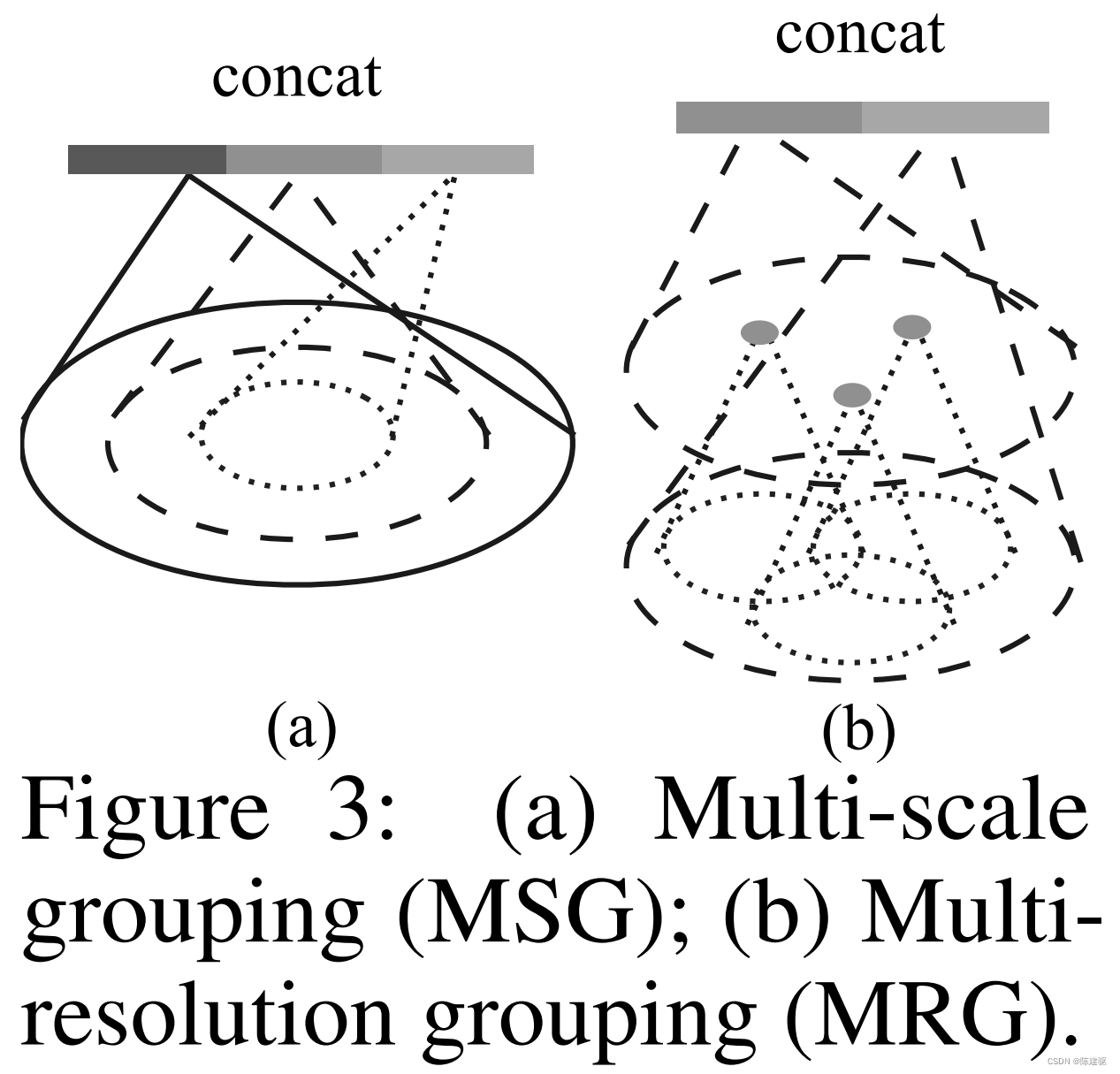
Multi-scale grouping (MSG)

? 如图3 (a)所示，一种简单而有效的捕获多尺度模式的方法是应用不同尺度的grouping层，然后根据PointNet提取每个尺度的特征。将不同尺度的特征串联起来形成多尺度特征。

? 随机输入dropout：在训练网络学习一种优化策略来结合多尺度特征。对每个实例以随机的概率随机dropout输入点。具体地说，对于每个训练点集，选择从$[0,p],p\le 1$ 中均匀采样一个dropout比例，记为 $\theta$ 。对于每个点用概率 $\theta$ 随机丢弃。在实现中设置 p = 0.95，以避免产生空的点集。通过这种方式，用各种稀疏性(由 $\theta$ 引起)和不同均匀性(由dropout的随机性引入)的训练集来表示网络。在测试时保留所有可用的点。

Multi-resolution grouping (MRG)

? MSG方法计算量很大，因为它为每个质心点在大尺度的邻域上运行局部PointNet。特别由于质心点的数量通常很大。而MRG减少了计算量，但保留了根据点的分布属性自适应聚合信息的能力。

? 如图3 (b)，某一层级区域的特征 $L_i$ 是两个向量的串联。利用set abstraction level，对较低层级 $L_{i?1}$ 的每个子区域的特征进行汇总，得到一个向量(图左)。另一个向量(右)是通过使用单个PointNet直接处理局部区域中的所有原始点而获得的特征。

? 当局部区域的密度较低时，第一个向量的可靠性可能不如第二个向量，因为计算第一个向量时的子区域包含的点更稀疏，更容易出现采样不足的情况。在这种情况下，第二个向量的权重应该更高。当局部区域的密度很高时，第一个向量提供了更详细的信息，因为它具有在较低水平上递归地以更高分辨率进行查看的能力。

? 与MSG相比，MRG在计算上更高效，因为它避免了在最低层级上大尺度邻域的特征提取。

点云分割的点特征递推

? 在set abstraction level，对原始点集进行下采样。而在点云分割任务中，如语义点云标注，我们希望得到所有原始点的点特征。一种解决方案是在所有集合的set abstraction level中，总是将所有点作为质心采样，但这导致了较高的计算量。另一种方法是将特征从下采样点递推回到原始点云。

? 这里采用基于距离插值的层级递推策略和skip连接(如下图)。

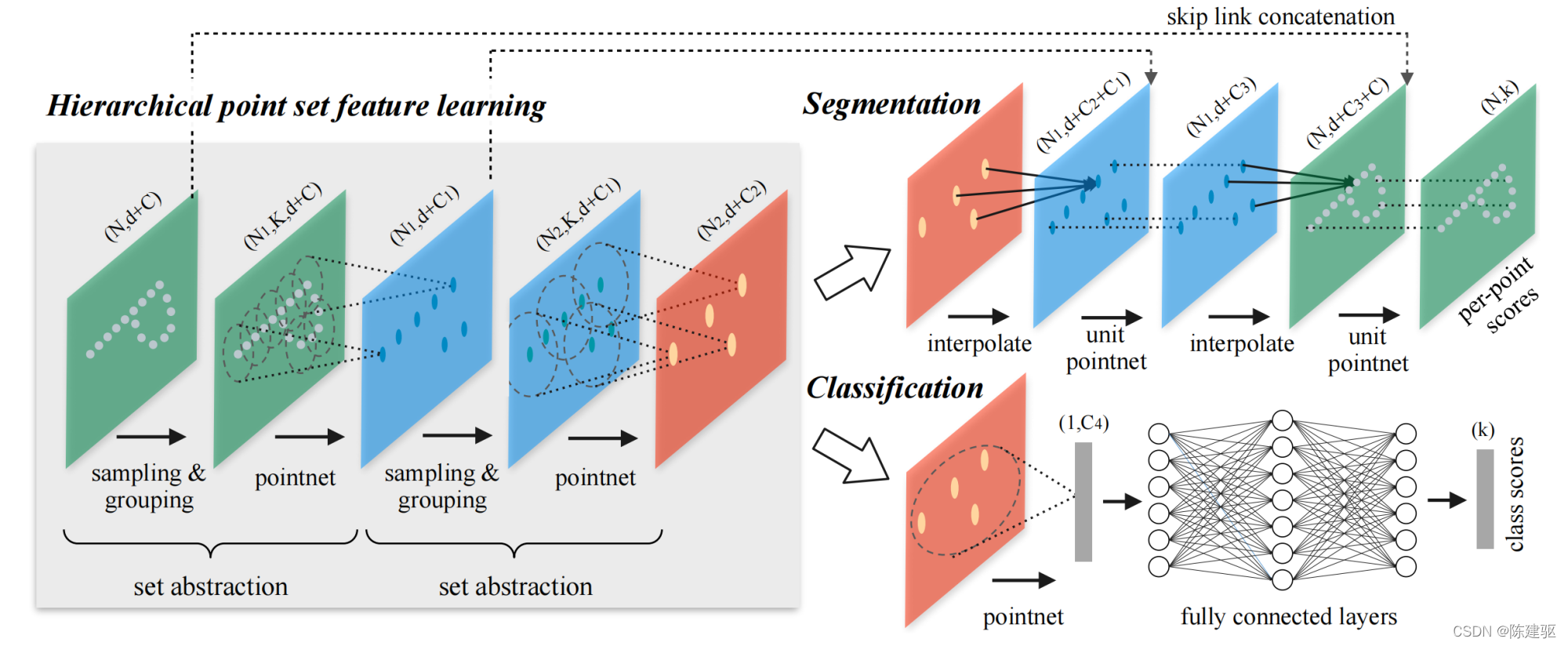
? 在特征递推层级(feature propagation level)，将 $N_l\times (d+C)$ 点集的特征 递推到 $N_{l?1}$ 个点，且 $N_l\le N_{l?1}$ ， $N_{l?1}$ 是set abstraction level的输入点数量， $N_l$ 是输出点数量。

? 通过在 $N_{l?1}$ 个点的坐标位置对 $N_l$ 个点特征进行插值实现特征递推。这里使用基于k个最近邻的逆距离加权平均实现插值，如上图所示。下式中，默认使用的 p=2,k=3。
$$f^{(j)}(x)=\frac{{\sum }_{i=1}^k{w}_i(x)f_i^{(j)}}{{\sum }_{i=1}^k{w}_i(x)}\text{where}{w}_i(x)=\frac{1}{d(x,x_i{)}^p},j=1,?,C\text{\hspace{1em}(2)}$$
? 然后将插值得到的特征与skip linked点特征串联，skip linked特征来自set abstraction level。然后将拼接后的特征通过一个unit pointnet，类似于CNN中的1x1卷积。利用少数共享的全连接层和ReLU层更新每个点的特征向量。这个过程不断重复，直到我们将特征递推到到原始的点集的大小。

实验

数据集

MNIST、Model-Net40、SHEREC15、ScanNet

点云分类实验

Robustness to Sampling Density Variation

? 直接获取的传感器数据通常存在严重的不规则采样问题(图1)。PointNet++选择多尺度的点邻域，通过适当加权，学习平衡描述性和鲁棒性。

? 在测试时dropout点(见图4左)，验证PointNet++对非均匀稀疏数据的鲁棒性。

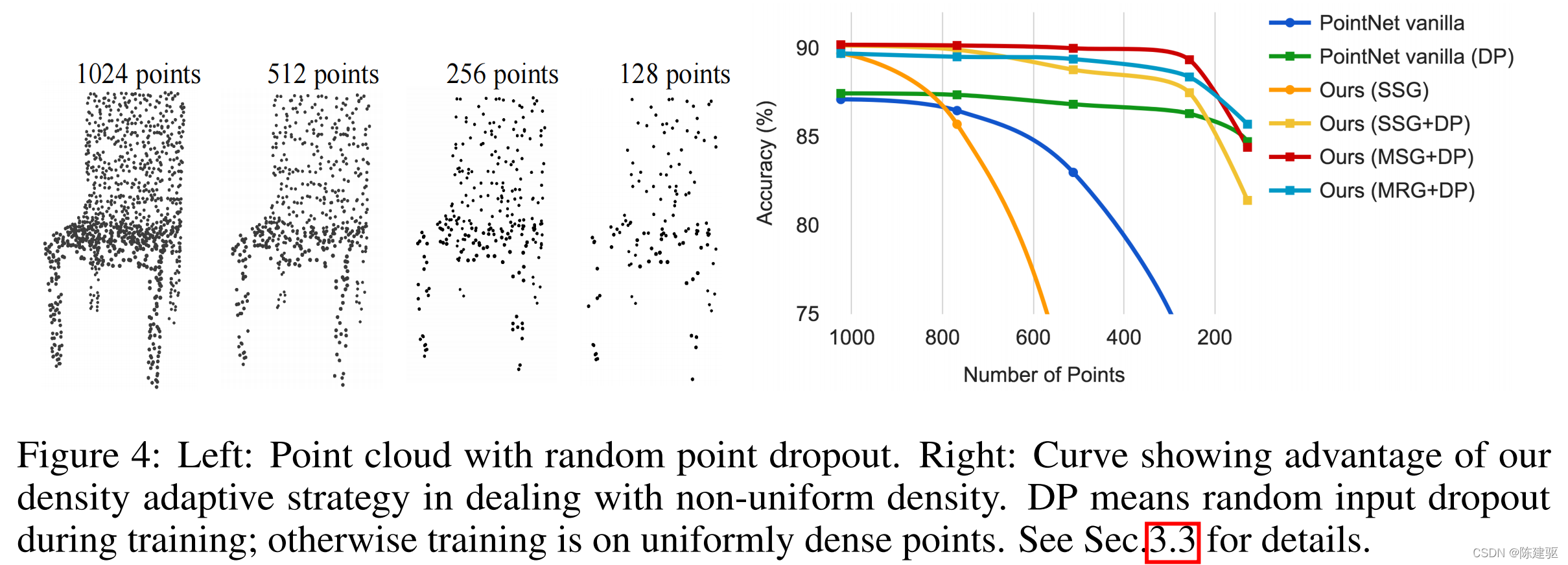
? 在图4右中，可以看到MSG+DP(训练时随机输入dropout的多尺度分组)和MRG+DP(训练时随机输入dropout的多分辨率分组)对采样密度变化非常鲁棒。MSG+DP性能下降不到1%，从1024到256测试点。此外，与其他方法相比，它在几乎所有的采样密度上都取得了最好的性能。

? PointNet在密度变化下相当鲁棒，因为它关注全局抽象而不是细节，然而细节的丢失也使得的精度不高。

? SSG(每层级单尺度分组的PointNet++)不能推广到稀疏采样密度，而SSG+DP通过在训练时间内随机丢点来弥补这一问题。

点云分割

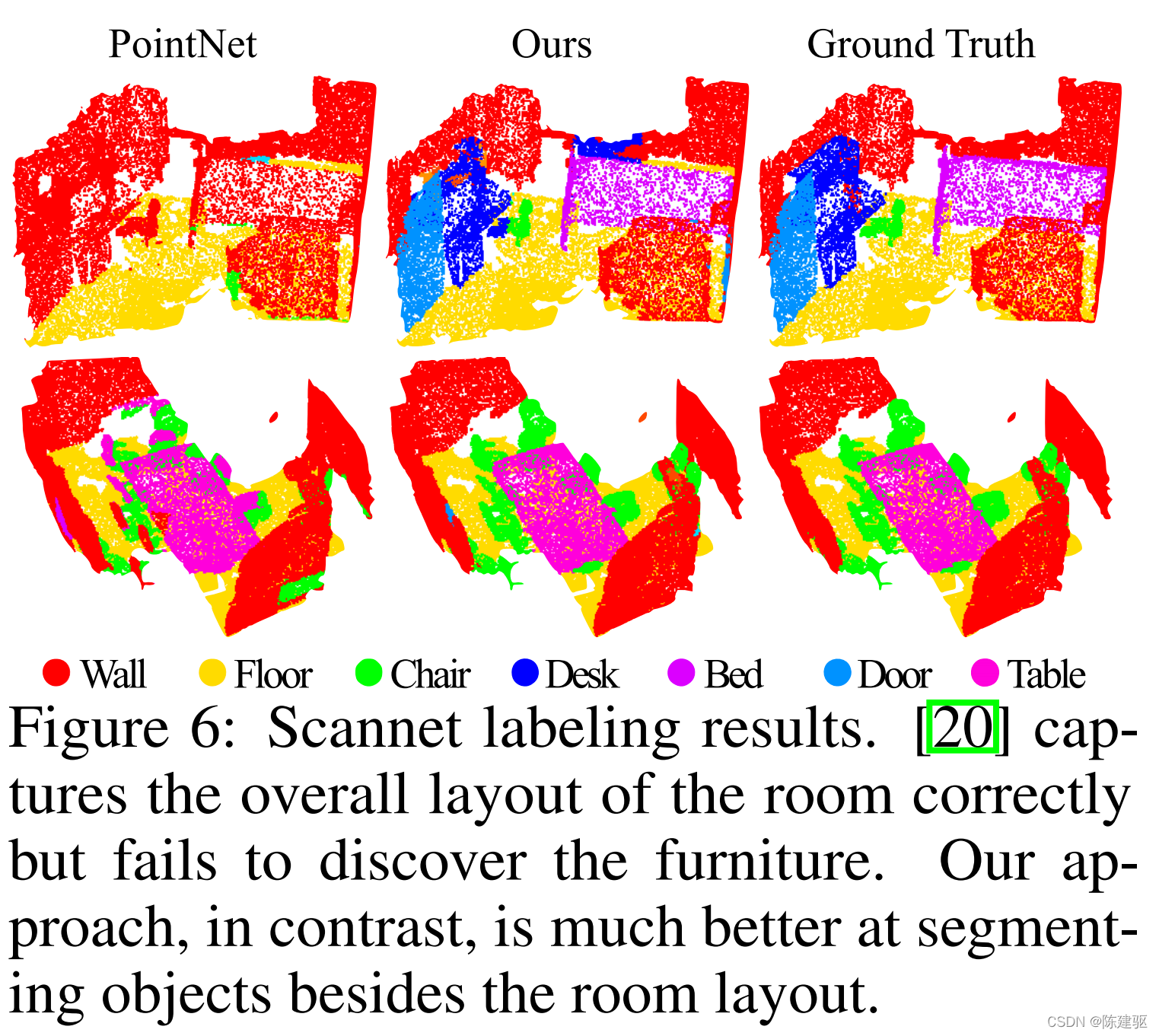
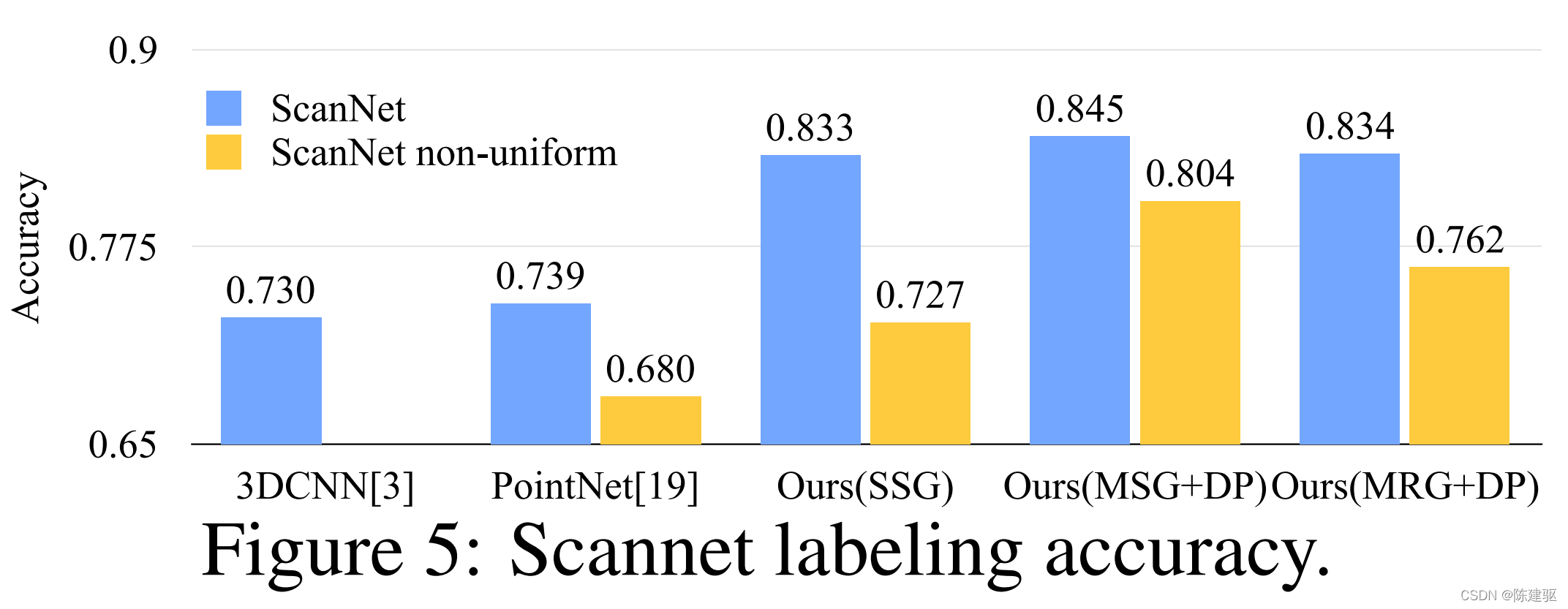
在非欧度量空间中点云分类

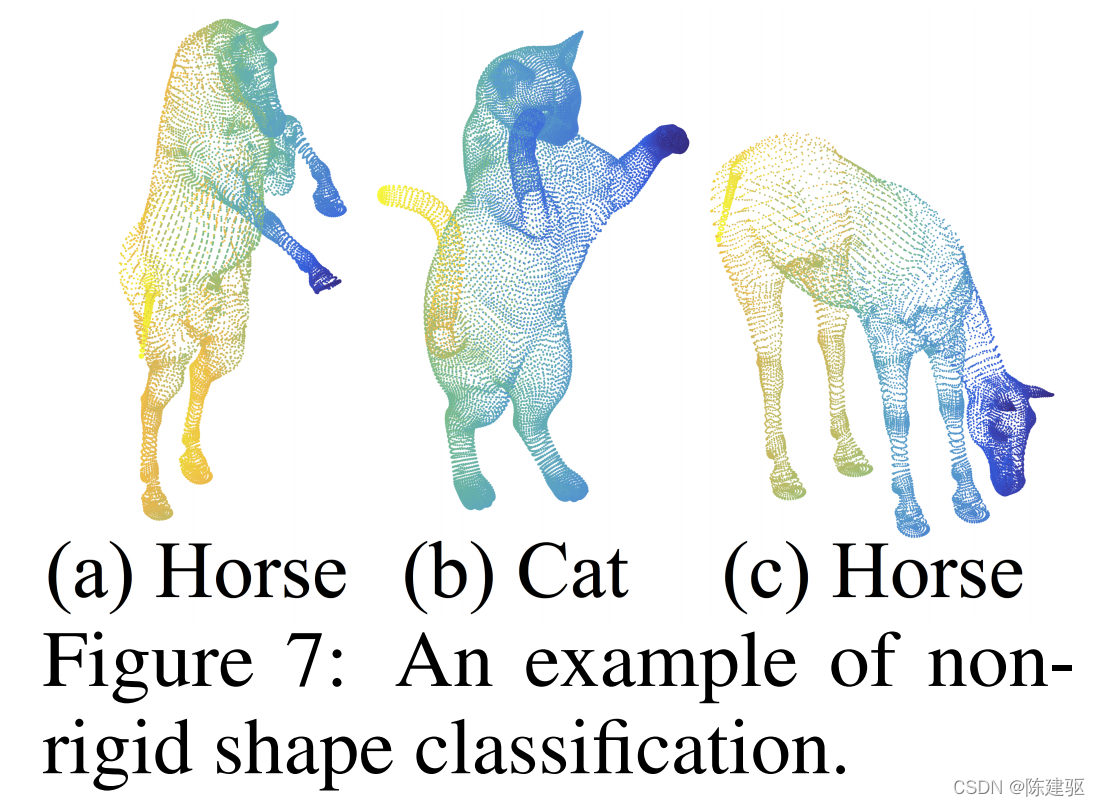
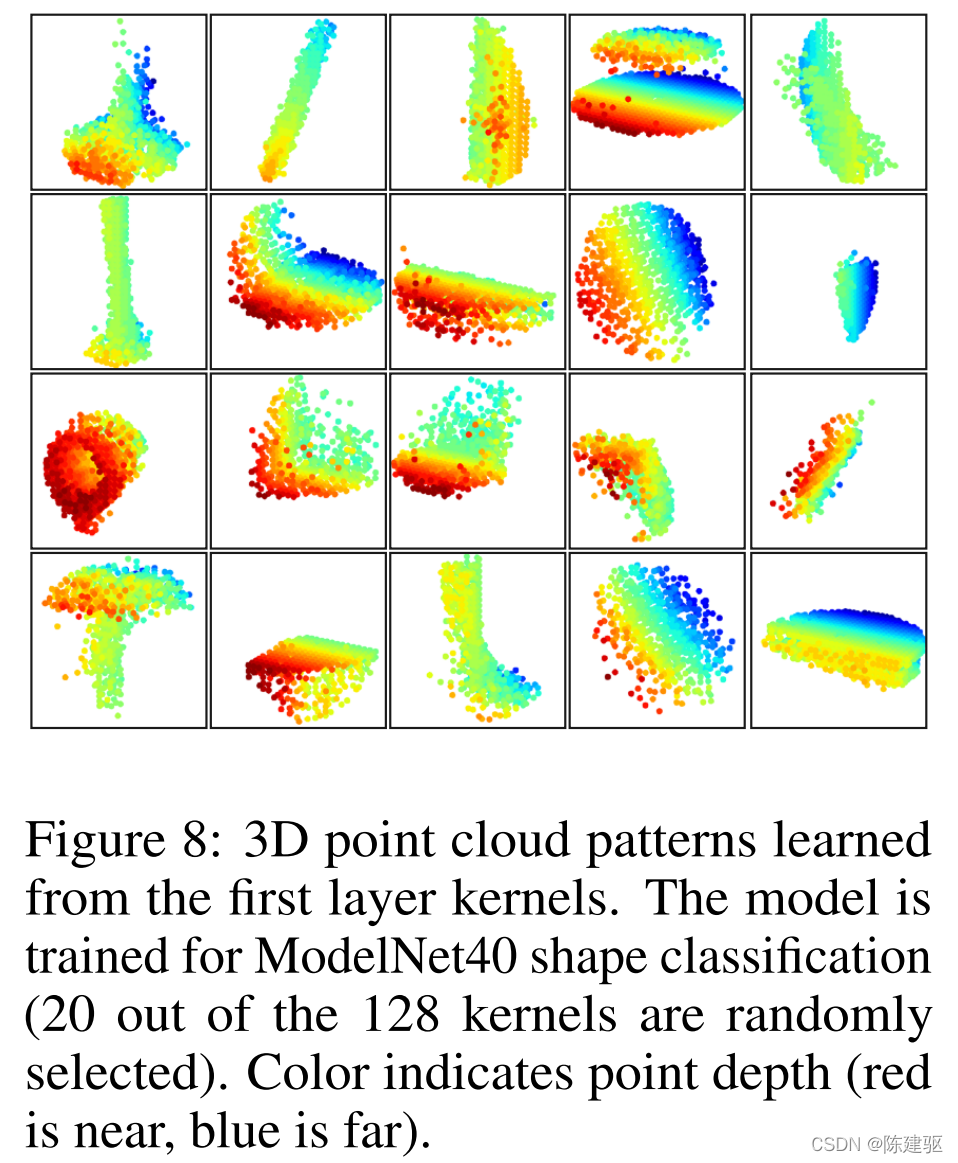
特征可视化

? 在图8中，我们将层级网络的第一级内核所学习的内容可视化。我们在空间中创建了一个体素网格，并聚集局部点集，在网格中最活跃的某些神经元(使用了最高100个示例)。选票高的网格被保留并转换回三维点云，这代表了神经元识别的模式。由于模型是在主要由家具组成的ModelNet40上训练的，所以在可视化中我们可以看到平面、双面、线、角等结构。

代码实现

yanx27/Pointnet_Pointnet2_pytorch: PointNet and PointNet++ implemented by pytorch (pure python) and on ModelNet, ShapeNet and S3DIS. (github.com)

最远点采样

def farthest_point_sample(xyz, npoint):
    """
    Input:
        xyz: pointcloud data, [B, N, 3]
        npoint: number of samples
    Return:
        centroids: sampled pointcloud index, [B, npoint]
    """
    device = xyz.device
    B, N, C = xyz.shape
    centroids = torch.zeros(B, npoint, dtype=torch.long).to(device)
    distance = torch.ones(B, N).to(device) * 1e10
    farthest = torch.randint(0, N, (B,), dtype=torch.long).to(device)#初始采样点
    batch_indices = torch.arange(B, dtype=torch.long).to(device)
    #采样npoint个点
    for i in range(npoint):
        centroids[:, i] = farthest
        centroid = xyz[batch_indices, farthest, :].view(B, 1, 3) #取出上一个采样点的位置
        dist = torch.sum((xyz - centroid) ** 2, -1)
        mask = dist < distance
        distance[mask] = dist[mask]
        farthest = torch.max(distance, -1)[1]
    return centroids

Ball query

def square_distance(src, dst):
    """
    Calculate Euclid distance between each two points.

    src^T * dst = xn * xm + yn * ym + zn * zm；
    sum(src^2, dim=-1) = xn*xn + yn*yn + zn*zn;
    sum(dst^2, dim=-1) = xm*xm + ym*ym + zm*zm;
    dist = (xn - xm)^2 + (yn - ym)^2 + (zn - zm)^2
         = sum(src**2,dim=-1)+sum(dst**2,dim=-1)-2*src^T*dst

    Input:
        src: source points, [B, N, C]
        dst: target points, [B, M, C]
    Output:
        dist: per-point square distance, [B, N, M]
    """
    B, N, _ = src.shape
    _, M, _ = dst.shape
    dist = -2 * torch.matmul(src, dst.permute(0, 2, 1))
    dist += torch.sum(src ** 2, -1).view(B, N, 1)
    dist += torch.sum(dst ** 2, -1).view(B, 1, M)
    return dist

def query_ball_point(radius, nsample, xyz, new_xyz):
    """
    Input:
        radius: local region radius
        nsample: max sample number in local region
        xyz: all points, [B, N, 3]
        new_xyz: query points, [B, S, 3]
    Return:
        group_idx: grouped points index, [B, S, nsample]
    """
    device = xyz.device
    B, N, C = xyz.shape
    _, S, _ = new_xyz.shape
    group_idx = torch.arange(N, dtype=torch.long).to(device).view(1, 1, N).repeat([B, S, 1])
    sqrdists = square_distance(new_xyz, xyz)
    group_idx[sqrdists > radius ** 2] = N
    group_idx = group_idx.sort(dim=-1)[0][:, :, :nsample]
    group_first = group_idx[:, :, 0].view(B, S, 1).repeat([1, 1, nsample])
    mask = group_idx == N
    group_idx[mask] = group_first[mask]
    return group_idx

采样和划分

def index_points(points, idx):
    """
    Input:
        points: input points data, [B, N, C]
        idx: sample index data, [B, S]
    Return:
        new_points:, indexed points data, [B, S, C]
    """
    device = points.device
    B = points.shape[0]
    view_shape = list(idx.shape)
    view_shape[1:] = [1] * (len(view_shape) - 1)
    repeat_shape = list(idx.shape)
    repeat_shape[0] = 1
    batch_indices = torch.arange(B, dtype=torch.long).to(device).view(view_shape).repeat(repeat_shape)
    new_points = points[batch_indices, idx, :]
    return new_points



def sample_and_group(npoint, radius, nsample, xyz, points, returnfps=False):
    """
    Input:
        npoint:
        radius:
        nsample:
        xyz: input points position data, [B, N, 3]
        points: input points data, [B, N, D]
    Return:
        new_xyz: sampled points position data, [B, npoint, nsample, 3]
        new_points: sampled points data, [B, npoint, nsample, 3+D]
    """
    B, N, C = xyz.shape
    S = npoint
    fps_idx = farthest_point_sample(xyz, npoint)  # [B, npoint, C]
    new_xyz = index_points(xyz, fps_idx)
    idx = query_ball_point(radius, nsample, xyz, new_xyz)
    grouped_xyz = index_points(xyz, idx)  # [B, npoint, nsample, C]
    grouped_xyz_norm = grouped_xyz - new_xyz.view(B, S, 1, C)

    if points is not None:
        grouped_points = index_points(points, idx)
        new_points = torch.cat([grouped_xyz_norm, grouped_points], dim=-1)  # [B, npoint, nsample, C+D]
    else:
        new_points = grouped_xyz_norm
    if returnfps:
        return new_xyz, new_points, grouped_xyz, fps_idx
    else:
        return new_xyz, new_points


def sample_and_group_all(xyz, points):
    """
    Input:
        xyz: input points position data, [B, N, 3]
        points: input points data, [B, N, D]
    Return:
        new_xyz: sampled points position data, [B, 1, 3]
        new_points: sampled points data, [B, 1, N, 3+D]
    """
    device = xyz.device
    B, N, C = xyz.shape
    new_xyz = torch.zeros(B, 1, C).to(device)
    grouped_xyz = xyz.view(B, 1, N, C)
    if points is not None:
        new_points = torch.cat([grouped_xyz, points.view(B, 1, N, -1)], dim=-1)
    else:
        new_points = grouped_xyz
    return new_xyz, new_points

集合抽象层的实现

class PointNetSetAbstraction(nn.Module):
    def __init__(self, npoint, radius, nsample, in_channel, mlp, group_all):
        super(PointNetSetAbstraction, self).__init__()
        self.npoint = npoint
        self.radius = radius
        self.nsample = nsample
        self.mlp_convs = nn.ModuleList()
        self.mlp_bns = nn.ModuleList()
        last_channel = in_channel
        for out_channel in mlp:
            self.mlp_convs.append(nn.Conv2d(last_channel, out_channel, 1))
            self.mlp_bns.append(nn.BatchNorm2d(out_channel))
            last_channel = out_channel
        self.group_all = group_all

    def forward(self, xyz, points):
        """
        Input:
            xyz: input points position data, [B, C, N]
            points: input points data, [B, D, N]
        Return:
            new_xyz: sampled points position data, [B, C, S]
            new_points_concat: sample points feature data, [B, D', S]
        """
        xyz = xyz.permute(0, 2, 1)
        if points is not None:
            points = points.permute(0, 2, 1)

        if self.group_all:
            new_xyz, new_points = sample_and_group_all(xyz, points)
        else:
            new_xyz, new_points = sample_and_group(self.npoint, self.radius, self.nsample, xyz, points)
        # new_xyz: sampled points position data, [B, npoint, C]
        # new_points: sampled points data, [B, npoint, nsample, C+D]
        new_points = new_points.permute(0, 3, 2, 1)  # [B, C+D, nsample,npoint]
        for i, conv in enumerate(self.mlp_convs):
            bn = self.mlp_bns[i]
            new_points = F.relu(bn(conv(new_points)))

        new_points = torch.max(new_points, 2)[0]
        new_xyz = new_xyz.permute(0, 2, 1)
        return new_xyz, new_points

多尺度集合抽象层(SMG)的实现

class PointNetSetAbstractionMsg(nn.Module):
    def __init__(self, npoint, radius_list, nsample_list, in_channel, mlp_list):
        super(PointNetSetAbstractionMsg, self).__init__()
        self.npoint = npoint
        self.radius_list = radius_list
        self.nsample_list = nsample_list
        self.conv_blocks = nn.ModuleList()
        self.bn_blocks = nn.ModuleList()
        for i in range(len(mlp_list)):
            convs = nn.ModuleList()
            bns = nn.ModuleList()
            last_channel = in_channel + 3
            for out_channel in mlp_list[i]:
                convs.append(nn.Conv2d(last_channel, out_channel, 1))
                bns.append(nn.BatchNorm2d(out_channel))
                last_channel = out_channel
            self.conv_blocks.append(convs)
            self.bn_blocks.append(bns)

    def forward(self, xyz, points):
        """
        Input:
            xyz: input points position data, [B, C, N]
            points: input points data, [B, D, N]
        Return:
            new_xyz: sampled points position data, [B, C, S]
            new_points_concat: sample points feature data, [B, D', S]
        """
        xyz = xyz.permute(0, 2, 1)
        if points is not None:
            points = points.permute(0, 2, 1)

        B, N, C = xyz.shape
        S = self.npoint
        new_xyz = index_points(xyz, farthest_point_sample(xyz, S))
        new_points_list = []
        for i, radius in enumerate(self.radius_list):
            K = self.nsample_list[i]
            group_idx = query_ball_point(radius, K, xyz, new_xyz)
            grouped_xyz = index_points(xyz, group_idx)
            grouped_xyz -= new_xyz.view(B, S, 1, C)
            if points is not None:
                grouped_points = index_points(points, group_idx)
                grouped_points = torch.cat([grouped_points, grouped_xyz], dim=-1)
            else:
                grouped_points = grouped_xyz

            grouped_points = grouped_points.permute(0, 3, 2, 1)  # [B, D, K, S]
            for j in range(len(self.conv_blocks[i])):
                conv = self.conv_blocks[i][j]
                bn = self.bn_blocks[i][j]
                grouped_points = F.relu(bn(conv(grouped_points)))
            new_points = torch.max(grouped_points, 2)[0]  # [B, D', S]
            new_points_list.append(new_points)

        new_xyz = new_xyz.permute(0, 2, 1)
        new_points_concat = torch.cat(new_points_list, dim=1)
        return new_xyz, new_points_concat

feature propogation

class PointNetFeaturePropagation(nn.Module):
    def __init__(self, in_channel, mlp):
        super(PointNetFeaturePropagation, self).__init__()
        self.mlp_convs = nn.ModuleList()
        self.mlp_bns = nn.ModuleList()
        last_channel = in_channel
        for out_channel in mlp:
            self.mlp_convs.append(nn.Conv1d(last_channel, out_channel, 1))
            self.mlp_bns.append(nn.BatchNorm1d(out_channel))
            last_channel = out_channel

    def forward(self, xyz1, xyz2, points1, points2):
        """
        Input:
            xyz1: input points position data, [B, C, N]
            xyz2: sampled input points position data, [B, C, S]
            points1: input points data, [B, D, N]
            points2: input points data, [B, D, S]
        Return:
            new_points: upsampled points data, [B, D', N]
        """
        xyz1 = xyz1.permute(0, 2, 1)
        xyz2 = xyz2.permute(0, 2, 1)

        points2 = points2.permute(0, 2, 1)
        B, N, C = xyz1.shape
        _, S, _ = xyz2.shape

        if S == 1:
            interpolated_points = points2.repeat(1, N, 1)
        else:
            dists = square_distance(xyz1, xyz2)
            dists, idx = dists.sort(dim=-1)
            dists, idx = dists[:, :, :3], idx[:, :, :3]  # [B, N, 3]

            dist_recip = 1.0 / (dists + 1e-8)
            norm = torch.sum(dist_recip, dim=2, keepdim=True)
            weight = dist_recip / norm
            interpolated_points = torch.sum(index_points(points2, idx) * weight.view(B, N, 3, 1), dim=2)

        if points1 is not None:
            points1 = points1.permute(0, 2, 1)
            new_points = torch.cat([points1, interpolated_points], dim=-1)
        else:
            new_points = interpolated_points

        new_points = new_points.permute(0, 2, 1)
        for i, conv in enumerate(self.mlp_convs):
            bn = self.mlp_bns[i]
            new_points = F.relu(bn(conv(new_points)))
        return new_points

PointNet++分类网络的实现

class get_model(nn.Module):
    def __init__(self,num_class,normal_channel=True):
        super(get_model, self).__init__()
        in_channel = 3 if normal_channel else 0
        self.normal_channel = normal_channel
        self.sa1 = PointNetSetAbstractionMsg(512, [0.1, 0.2, 0.4], [16, 32, 128], in_channel,[[32, 32, 64], [64, 64, 128], [64, 96, 128]])
        self.sa2 = PointNetSetAbstractionMsg(128, [0.2, 0.4, 0.8], [32, 64, 128], 320,[[64, 64, 128], [128, 128, 256], [128, 128, 256]])
        self.sa3 = PointNetSetAbstraction(None, None, None, 640 + 3, [256, 512, 1024], True)
        self.fc1 = nn.Linear(1024, 512)
        self.bn1 = nn.BatchNorm1d(512)
        self.drop1 = nn.Dropout(0.4)
        self.fc2 = nn.Linear(512, 256)
        self.bn2 = nn.BatchNorm1d(256)
        self.drop2 = nn.Dropout(0.5)
        self.fc3 = nn.Linear(256, num_class)

    def forward(self, xyz):
        B, _, _ = xyz.shape
        if self.normal_channel:
            norm = xyz[:, 3:, :]
            xyz = xyz[:, :3, :]
        else:
            norm = None
        l1_xyz, l1_points = self.sa1(xyz, norm)
        l2_xyz, l2_points = self.sa2(l1_xyz, l1_points)
        l3_xyz, l3_points = self.sa3(l2_xyz, l2_points)
        x = l3_points.view(B, 1024)
        x = self.drop1(F.relu(self.bn1(self.fc1(x))))
        x = self.drop2(F.relu(self.bn2(self.fc2(x))))
        x = self.fc3(x)
        x = F.log_softmax(x, -1)

PointNet++分割网络的实现

class get_model(nn.Module):
    def __init__(self, num_classes):
        super(get_model, self).__init__()

        self.sa1 = PointNetSetAbstractionMsg(1024, [0.05, 0.1], [16, 32], 9, [[16, 16, 32], [32, 32, 64]])
        self.sa2 = PointNetSetAbstractionMsg(256, [0.1, 0.2], [16, 32], 32+64, [[64, 64, 128], [64, 96, 128]])
        self.sa3 = PointNetSetAbstractionMsg(64, [0.2, 0.4], [16, 32], 128+128, [[128, 196, 256], [128, 196, 256]])
        self.sa4 = PointNetSetAbstractionMsg(16, [0.4, 0.8], [16, 32], 256+256, [[256, 256, 512], [256, 384, 512]])
        self.fp4 = PointNetFeaturePropagation(512+512+256+256, [256, 256])
        self.fp3 = PointNetFeaturePropagation(128+128+256, [256, 256])
        self.fp2 = PointNetFeaturePropagation(32+64+256, [256, 128])
        self.fp1 = PointNetFeaturePropagation(128, [128, 128, 128])
        self.conv1 = nn.Conv1d(128, 128, 1)
        self.bn1 = nn.BatchNorm1d(128)
        self.drop1 = nn.Dropout(0.5)
        self.conv2 = nn.Conv1d(128, num_classes, 1)

    def forward(self, xyz):
        l0_points = xyz
        l0_xyz = xyz[:,:3,:]

        l1_xyz, l1_points = self.sa1(l0_xyz, l0_points)
        l2_xyz, l2_points = self.sa2(l1_xyz, l1_points)
        l3_xyz, l3_points = self.sa3(l2_xyz, l2_points)
        l4_xyz, l4_points = self.sa4(l3_xyz, l3_points)

        l3_points = self.fp4(l3_xyz, l4_xyz, l3_points, l4_points)
        l2_points = self.fp3(l2_xyz, l3_xyz, l2_points, l3_points)
        l1_points = self.fp2(l1_xyz, l2_xyz, l1_points, l2_points)
        l0_points = self.fp1(l0_xyz, l1_xyz, None, l1_points)

        x = self.drop1(F.relu(self.bn1(self.conv1(l0_points))))
        x = self.conv2(x)
        x = F.log_softmax(x, dim=1)
        x = x.permute(0, 2, 1)
        return x, l4_points


class get_loss(nn.Module):
    def __init__(self):
        super(get_loss, self).__init__()
    def forward(self, pred, target, trans_feat, weight):
        total_loss = F.nll_loss(pred, target, weight=weight)

        return total_loss