在第 3 节中,我们介绍了 softmax 回归(第 3.4 节),从头开始实现算法(第 3.6 节)并使用高级 API(第 3.7 节),并训练分类器从低分辨率图像中识别 10 种服装类别。在此过程中,我们学习了如何处理数据,将我们的输出强制转换为有效的概率分布,应用适当的损失函数,并根据我们的模型参数将其最小化。现在我们已经在简单线性模型的背景下掌握了这些机制,我们可以开始探索深度神经网络,这是本书主要关注的相对丰富的模型类别。
4.1.1 隐藏层
我们已经在 第 3.1.1.1 节中描述了仿射变换,它是一个添加了偏差的线性变换。首先,回顾一下与我们的 softmax 回归示例对应的模型架构,如图 3.4.1 所示。该模型通过单个仿射变换将我们的输入直接映射到我们的输出,然后是 softmax 操作。如果我们的标签确实通过仿射变换与我们的输入数据相关,那么这种方法就足够了。但是仿射变换中的线性是一个强有力的假设。
4.1.1.1 线性模型可能会出错
例如,线性意味着单调性的较弱假设 :我们的特征的任何增加都必须总是导致我们模型的输出增加(如果相应的权重为正),或者总是导致我们模型的输出减少(如果相应的权重为负)。有时这是有道理的。例如,如果我们试图预测一个人是否会偿还贷款,我们可以合理地想象,在其他条件相同的情况下,收入较高的申请人总是比收入较低的申请人更有可能偿还贷款。虽然单调,但这种关系可能与还款概率不是线性相关的。收入从 0 增加到 50000 可能对应的还款可能性比从 100 万增加到 105 万更大。处理这个问题的一种方法可能是预处理我们的数据,使线性变得更加合理,
请注意,我们可以很容易地提出违反单调性的示例。例如,我们想根据体温预测死亡概率。对于体温高于 37°C (98.6°F) 的人,温度越高表明风险越大。然而,对于体温低于 37°C 的人来说,较高的温度表明较低的风险!在这种情况下,我们也可以通过一些巧妙的预处理来解决问题。也就是说,我们可以使用距 37°C 的距离作为我们的特征。
但是对猫和狗的图像进行分类呢?增加位置 (13, 17) 的像素强度是否应该总是增加(或总是减少)图像描绘狗的可能性?对线性模型的依赖对应于隐含的假设,即区分猫与狗的唯一要求是评估单个像素的亮度。在反转图像保留类别的世界中,这种方法注定会失败。
然而,尽管这里的线性显然很荒谬,但与我们之前的示例相比,我们可以通过简单的预处理修复来解决问题并不那么明显。这是因为任何像素的重要性以复杂的方式取决于其上下文(周围像素的值)。虽然我们的数据可能存在一种表示,它会考虑到我们的特征之间的相关交互,在此之上线性模型是合适的,但我们根本不知道如何手动计算它。通过深度神经网络,我们使用观察数据来共同学习通过隐藏层的表示和作用于该表示的线性预测器。
4.1.1.2 合并隐藏层
我们可以通过合并一个或多个隐藏层来克服线性模型的这些限制并处理更通用的函数类别。最简单的方法是将许多完全连接的层堆叠在一起。每一层都馈入它上面的层,直到我们生成输出。我们可以想到第一个L -1 层作为我们的表示,最后一层作为我们的线性预测器。这种架构通常称为多层感知器,通常缩写为MLP。下面,我们用图表描述了一个 MLP(图 4.1.1)。
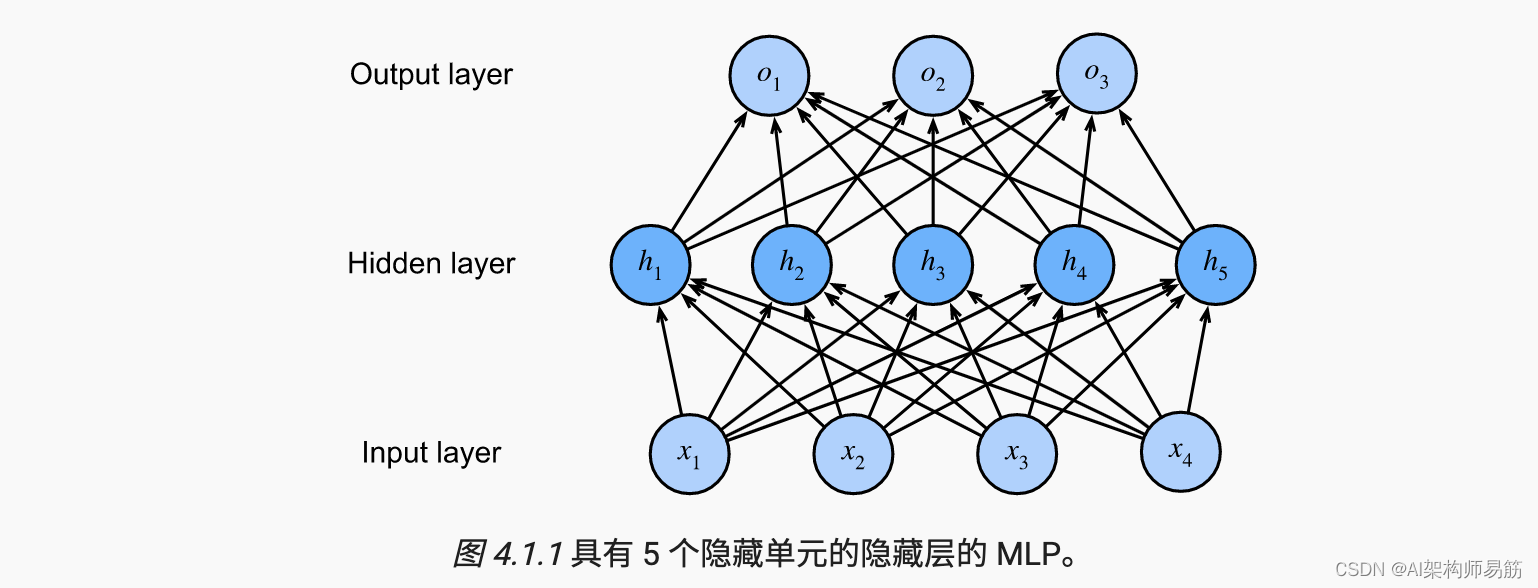
这个 MLP 有 4 个输入,3 个输出,它的隐藏层包含 5 个隐藏单元。由于输入层不涉及任何计算,因此使用该网络产生输出需要同时实现隐藏层和输出层的计算;因此,此 MLP 中的层数为 2。请注意,这些层都是全连接的。每个输入都会影响隐藏层中的每个神经元,而这些中的每一个又会影响输出层中的每个神经元。然而,正如 第 3.4.3 节所建议的那样,具有完全连接层的 MLP 的参数化成本可能非常高,即使不改变输入或输出大小,这也可能会促使参数保存和模型有效性之间进行权衡 [Zhang et al., 2021 ] .
4.1.1.3 从线性到非线性

请注意,添加隐藏层后,我们的模型现在需要我们跟踪和更新额外的参数集。作为交换, 那么我们得到了什么?您可能会惊讶地发现——在上面定义的模型中——我们的问题没有得到解决!原因很简单。上面的隐藏单元由输入的仿射函数给出,输出(pre-softmax)只是隐藏单元的仿射函数。仿射函数的仿射函数本身就是仿射函数。此外,我们的线性模型已经能够表示任何仿射函数。

由于每一行X在对应于小批量中的一个例子,有一些符号滥用,我们定义非线性激活函数σ 以逐行方式应用于其输入,即一次一个示例。请注意,我们在第 3.4.5 节中以相同的方式使用 softmax 表示法来表示逐行操作 。通常,如本节所述,我们应用于隐藏层的激活函数不仅是逐行的,而且是逐元素的。这意味着在计算层的线性部分之后,我们可以计算每个激活,而无需查看其他隐藏单元的值。大多数激活函数都是如此。

4.1.1.4。通用逼近器
MLP 可以通过隐藏的神经元捕获我们输入之间的复杂交互,这取决于每个输入的值。我们可以很容易地设计隐藏节点来执行任意计算,例如,对一对输入的基本逻辑操作。此外,对于激活函数的某些选择,众所周知,MLP 是通用逼近器。即使使用单隐藏层网络,给定足够多的节点(可能很多)和正确的权重集,我们也可以对任何函数进行建模,尽管实际上学习该函数是困难的部分。您可能会认为您的神经网络有点像 C 编程语言。与任何其他现代语言一样,该语言能够表达任何可计算的程序。但实际上提出一个符合您的规范的程序是困难的部分。
此外,仅仅因为单隐藏层网络可以学习任何功能并不意味着您应该尝试使用单隐藏层网络解决所有问题。事实上,我们可以通过使用更深(相??对于更宽)网络更紧凑地逼近许多函数。我们将在随后的章节中触及更严格的论点。
4.1.2. 激活函数
激活函数通过计算加权和并进一步添加偏差来决定是否应该激活神经元。它们是将输入信号转换为输出的可微算子,而它们中的大多数都增加了非线性。因为激活函数是深度学习的基础,所以让我们简要介绍一些常见的激活函数。
%matplotlib inline
import torch
from d2l import torch as d2l
4.1.2.1 ReLU 函数
由于实现的简单性和在各种预测任务上的良好性能,最受欢迎的选择是整流线性单元( ReLU )。ReLU 提供了一个非常简单的非线性变换。给定一个元素x,该函数被定义为max(x,0):
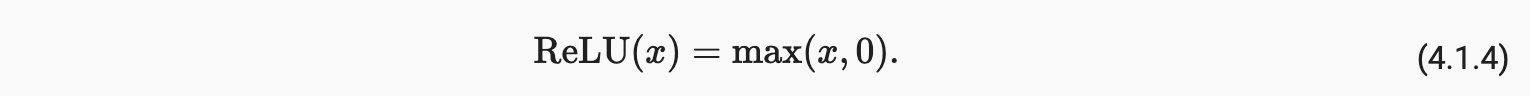
非正式地,ReLU 函数只保留正元素并通过将相应的激活设置为 0 来丢弃所有负元素。为了获得一些直觉,我们可以绘制函数。如您所见,激活函数是分段线性的。
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y = torch.relu(x)
d2l.plot(x.detach(), y.detach(), 'x', 'relu(x)', figsize=(5, 2.5))
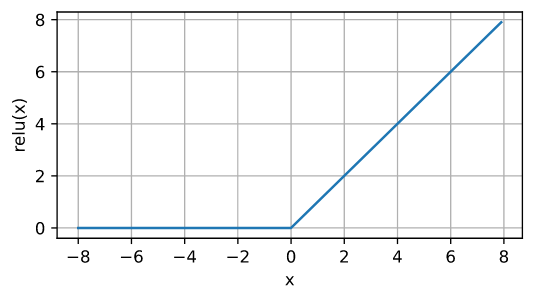
当输入为负时,ReLU 函数的导数为 0,当输入为正时,ReLU 函数的导数为 1。请注意,当输入值精确等于 0 时,ReLU 函数不可微。在在这些情况下,我们默认使用左侧导数,并说当输入为 0 时导数为 0。我们可以摆脱这种情况,因为输入实际上可能永远不会为零。有一句古老的格言,如果微妙的边界条件很重要,我们可能在做(真正的)数学,而不是工程。传统智慧可能适用于此。我们绘制了下面绘制的 ReLU 函数的导数。
y.backward(torch.ones_like(x), retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of relu', figsize=(5, 2.5))
使用 ReLU 的原因是它的导数表现特别好:它们要么消失,要么只是让论证通过。这使得优化表现得更好,并且它缓解了困扰先前版本的神经网络的有据可查的梯度消失问题(稍后会详细介绍)。
请注意,ReLU 函数有许多变体,包括 参数化 ReLU ( pReLU ) 函数[He et al., 2015]。这种变化为 ReLU 添加了一个线性项,因此即使参数为负,一些信息仍然可以通过:
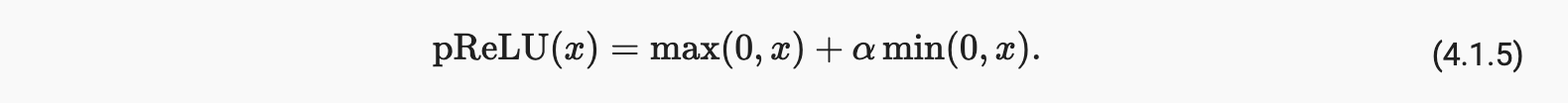
4.1.2.2 Sigmoid 函数

在最早的神经网络中,科学家们对模拟生物神经元或激发或不激发感兴趣。因此,这一领域的先驱们,可以追溯到人工神经元的发明者 McCulloch 和 Pitts,专注于阈值单元。阈值激活在其输入低于某个阈值时取值为 0,当输入超过阈值时取值为 1。
当注意力转移到基于梯度的学习上时,sigmoid 函数是一个自然的选择,因为它是阈值单元的平滑、可微近似。当我们想要将输出解释为二进制分类问题的概率时,Sigmoid 仍然被广泛用作输出单元的激活函数(您可以将 sigmoid 视为 softmax 的一个特例)。然而,大部分用于隐藏层的 Sigmoid 已被更简单且更易于训练的 ReLU 所取代。在后面关于循环神经网络的章节中,我们将描述利用 sigmoid 单元来控制跨时间信息流的架构。
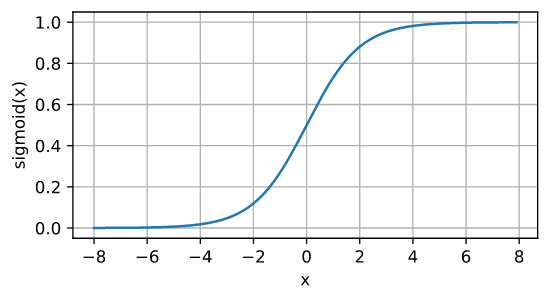
下面,我们绘制 sigmoid 函数。请注意,当输入接近 0 时,sigmoid 函数接近线性变换。
y = torch.sigmoid(x)
d2l.plot(x.detach(), y.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
sigmoid 函数的导数由以下等式给出:
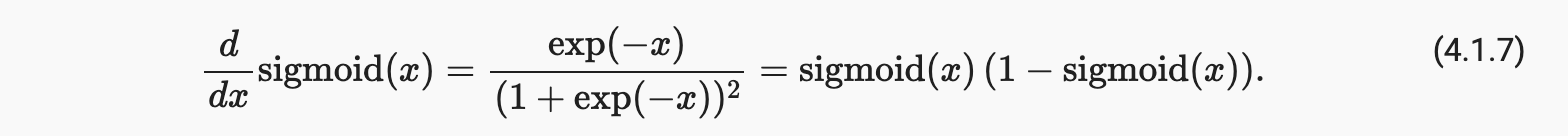
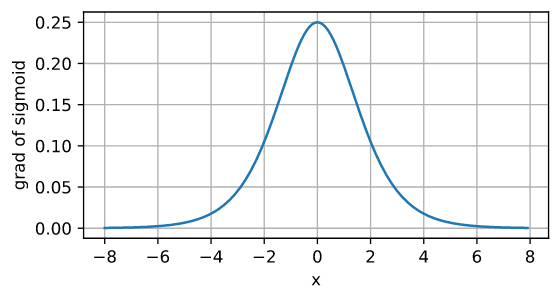
sigmoid 函数的导数如下图所示。注意当输入为0时,sigmoid函数的导数达到最大值0.25。随着输入在任一方向上从 0 发散,导数接近 0。
# Clear out previous gradients
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of sigmoid', figsize=(5, 2.5))
4.1.2.3 正切函数
与 sigmoid 函数一样,tanh(双曲正切)函数也会压缩其输入,将它们转换为介于 -1 和 1 之间的元素:
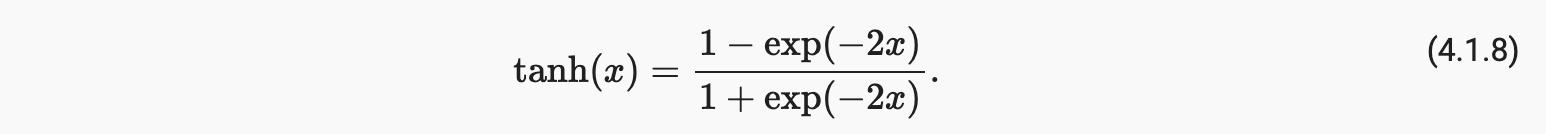
我们在下面绘制了 tanh 函数。请注意,当输入接近 0 时,tanh 函数接近线性变换。虽然函数的形状类似于 sigmoid 函数,但 tanh 函数表现出关于坐标系原点的点对称性。
y = torch.tanh(x)
d2l.plot(x.detach(), y.detach(), 'x', 'tanh(x)', figsize=(5, 2.5))
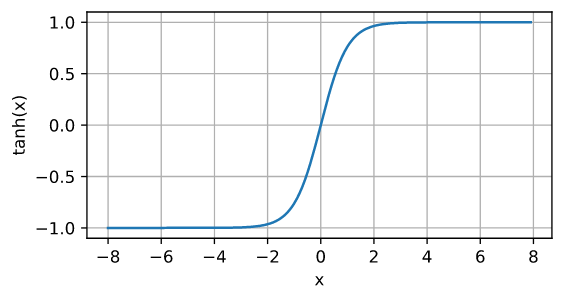
tanh 函数的导数是:
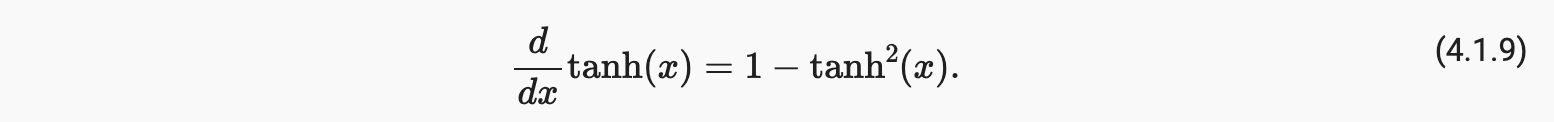
tanh 函数的导数如下图所示。当输入接近 0 时,tanh 函数的导数接近最大值 1。正如我们在 sigmoid 函数中看到的那样,随着输入在任一方向上远离 0,tanh 函数的导数接近 0。
# Clear out previous gradients.
x.grad.data.zero_()
y.backward(torch.ones_like(x),retain_graph=True)
d2l.plot(x.detach(), x.grad, 'x', 'grad of tanh', figsize=(5, 2.5))
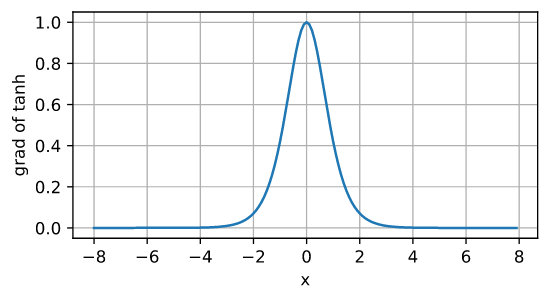
总之,我们现在知道如何结合非线性来构建富有表现力的多层神经网络架构。附带说明一下,您的知识已经使您掌握了与 1990 年左右的从业者类似的工具包。在某些方面,您比 1990 年代工作的任何人都具有优势,因为您可以利用强大的开源深度学习框架来构建只需几行代码即可快速建模。以前,训练这些网络需要研究人员编写数千行 C 和 Fortran 代码。
4.1.3 概括
-
MLP 在输出层和输入层之间添加一个或多个全连接隐藏层,并通过激活函数转换隐藏层的输出。
-
常用的激活函数包括 ReLU 函数、sigmoid 函数和 tanh 函数。
4.1.4。练习
-
- 计算 pReLU 激活函数的导数。
the derivative of the tanh:
- 计算 pReLU 激活函数的导数。
dtanh(x)/dx=1?tanh^(2)=
{2exp(?2x)-[exp(?2x)]^2}/(1+exp(?2x))^2.
https://www.math24.net/derivatives-hyperbolic-functions/
the derivative of the pReLU(x):
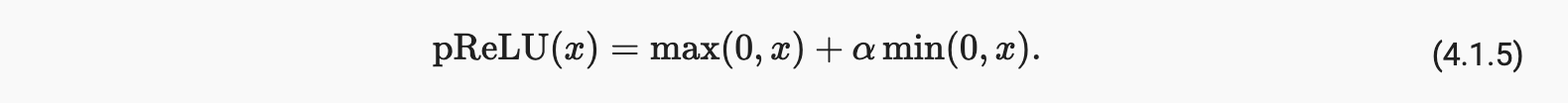
-
dpReLU(x)/dx = 1(ifx > 0); -
α (if
x < 0); -
doesn’t exist (if
x = 0) -
- 证明仅使用 ReLU(或 pReLU)的 MLP 构造了一个连续的分段线性函数。
h= ReLU(x) = max(x, 0)
y = ReLU(h) = max(h, 0) = max(x, 0) =ReLU(x)
h= pReLU(x)=max(0,x)+αmin(0,x).
y = pReLU(h) =max(0,h)+αmin(0,h)
One linear functions add,minus other linear function still is linear function.
-
- 显示
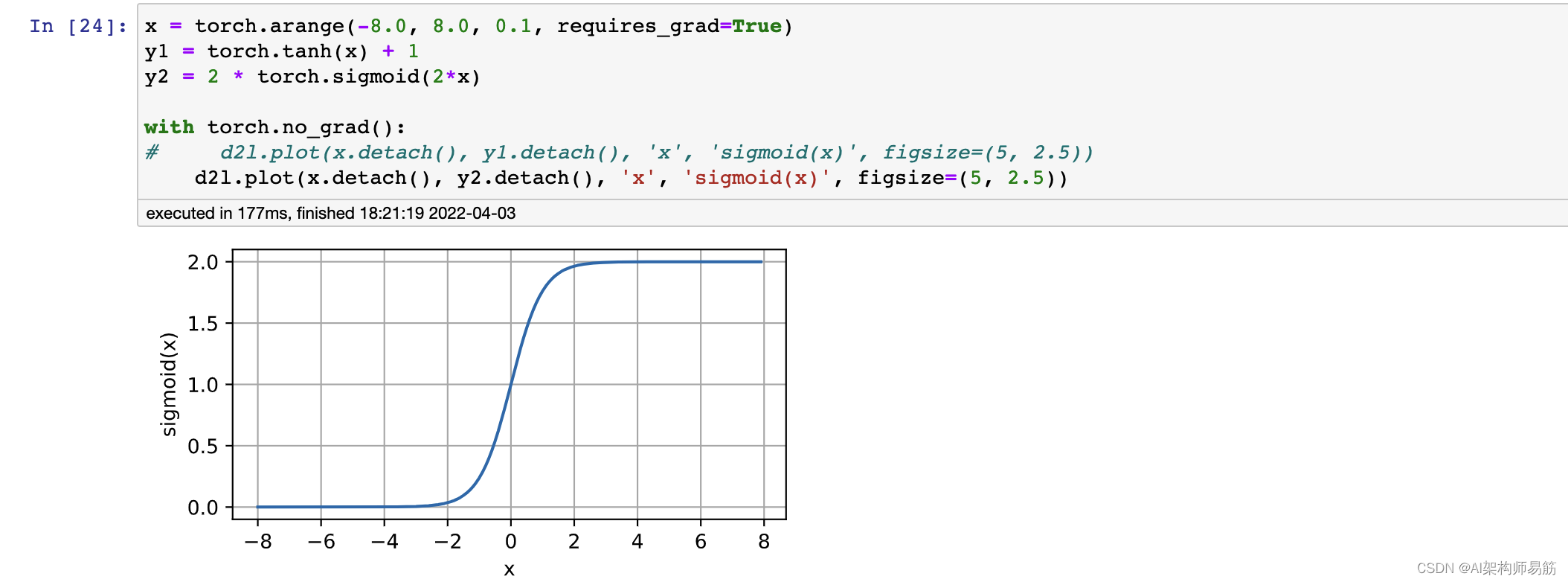
tanh(x) + 1 = 2 sigmoid(2x)
- 显示
[1?exp(?2x)]/[1+exp(?2x)]+1 = 2/[1+exp(?2x)] = 2 * 1/[1+exp(?2x)] = 2 sigmoid(2x)
x = torch.arange(-8.0, 8.0, 0.1, requires_grad=True)
y1 = torch.tanh(x) + 1
y2 = 2 * torch.sigmoid(2*x)
with torch.no_grad():
d2l.plot(x.detach(), y1.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
d2l.plot(x.detach(), y2.detach(), 'x', 'sigmoid(x)', figsize=(5, 2.5))
-
- 假设我们有一个非线性,一次只适用于一个小批量。你预计这会导致什么样的问题?
参考
https://d2l.ai/chapter_multilayer-perceptrons/mlp.html