[人工智能]偏差，方差，正则项

偏差与方差

偏差反应了命中程度，方差反应了离散程度。模型拟合程度越高，过拟合是低偏差，高方差。一般地，
$$模型误差=方差+偏差+不可避免误差(数据噪声)$$

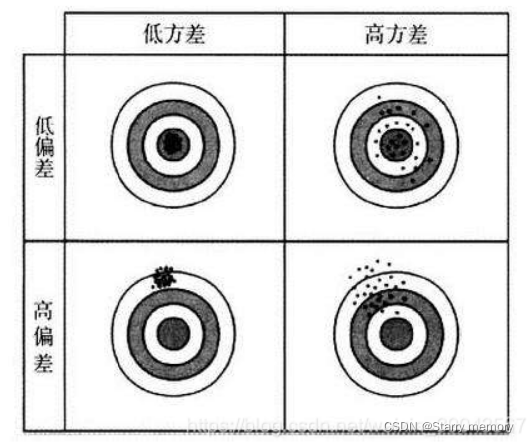
上述标靶是从其它博客中拷贝过来的，见

https://www.cxyzjd.com/article/weixin_39043567/92763286

命中标靶越高，说明准确率越高。

正则项

一般地，我们优化$MSE$

$$l_{mse}=\frac{{\sum }_i(y_i?{\hat{y}}_i{)}^2}{n}$$

为了使参数尽可能小，加入正则项，防止过拟合，减小方差。L1正则可以更容易得到稀疏项。这一点可以降低参数量举个例子。例如我们的参数只有$w_1$和$w_2$，那么我们的目标是让损失为0，如果损失为0，L1正则对应的是菱形，L2正则对应的是圆，$MSE$损失函数对应的是偏离原点的椭圆，是关于椭圆的平移变换。

$$l_{mse}+|w_1|+|w_2|=0$$
则
$$l_{mse}=?(|w_1|+|w_2|)$$

$?(|w_1|+|w_2|)$表示一个菱形，与$l_{mse}$的交点可以更容易使得$w_1$和$w_2$为0，得到稀疏性。

注：上述这一部分可以参考西瓜书253页