0. introduction

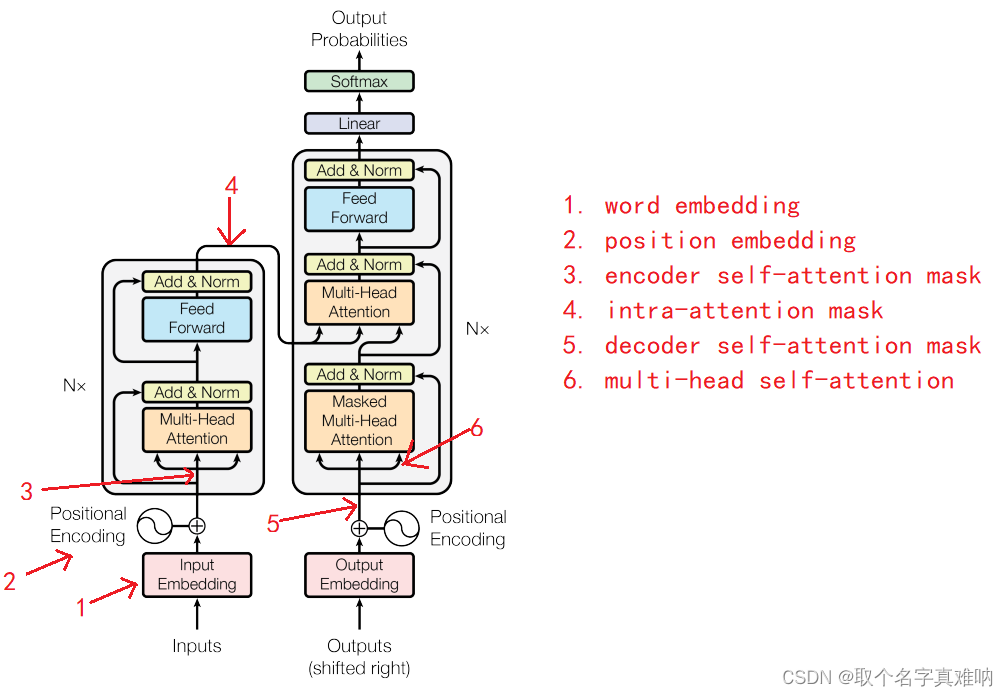
由图可知，Transformer结构是由Encoder-Decoder结构组成，为了更好的完成Transformer神经网络的训练，我们需要对每个路径下进行mark处理，这样就能更好的完成数据的训练和数据梯度的更新。
在这里插入图片描述

1. word embedding

1.1 将words标准化处理

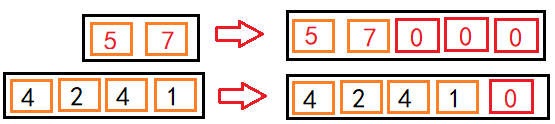
在这里插入图片描述
因为输入模型的句子source_sentence和输出模型的句子target_sentence不一致，所以为了保证模型的训练，我们需要将模型的句子进行填充padding操作，这样我们就能够很好的训练模型数据，

import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F

# 目标：word_embedding
# 考虑source sentence和 target sentence
# 对原始数据长度进行填充操作，
# 最后不同长度的源句子和目标句子整合成同等长度的句子
# 构建序列，序列的字符以其在词表中的索引的形式表示

# 定义源句子的长度source_length,目标句子的长度 target_length
src_len = torch.Tensor([2, 4]).to(torch.int32)
tgt_len = torch.Tensor([4, 3]).to(torch.int32)

# 定义相关参数
# 批量大小
batch_size = 2


# 序列的最大长度
max_src_seq_len = 5
max_tgt_seq_len = 5

# 定义单词表的大小
max_num_src_words = 8
max_num_tgt_words = 8

# 1.将不同长度的源句子填充成统一长度/
# 2.将源句子张量按行堆叠起来
# src_seq 单词索引构成的句子

src_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_src_words, (L,)), (0, max_src_seq_len - L)), 0) for L in src_len], 0)
tgt_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_tgt_words, (L,)), (0, max_tgt_seq_len - L)), 0) for L in tgt_len], 0)
print(f"src_seq=\n{src_seq}")
print(f"tgt_seq=\n{tgt_seq}")

# src_seq=
# tensor([[5, 7, 0, 0, 0],
#         [4, 2, 4, 1, 0]])
# tgt_seq=
# tensor([[1, 1, 1, 6, 0],
#         [1, 5, 5, 0, 0]])

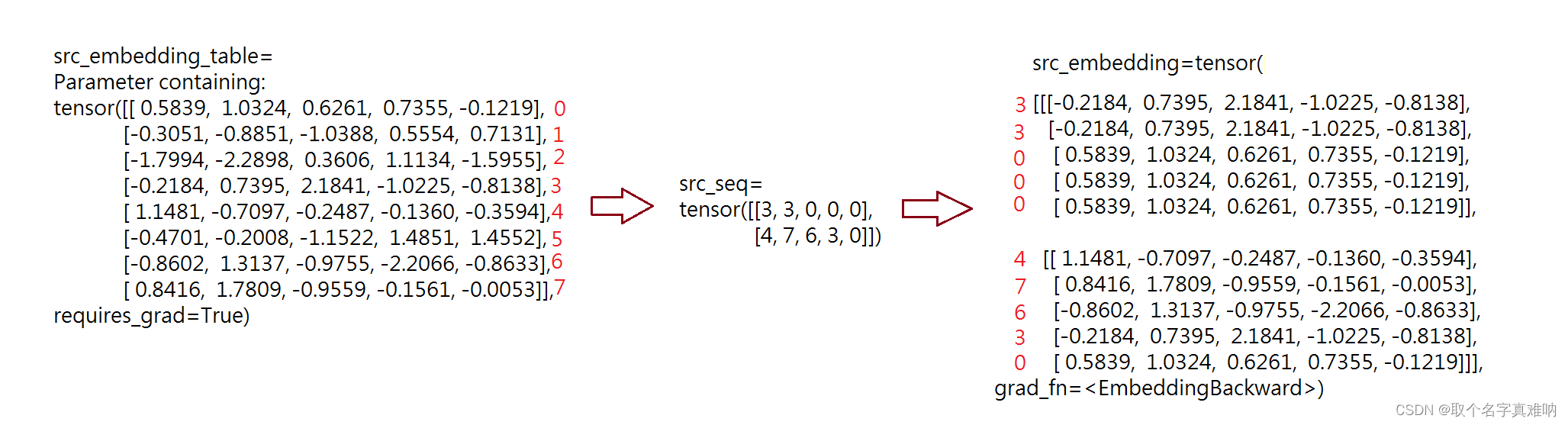
1.2 构造Word_Embedding

将填充好的源序列序号依次从对应的单词表中取出对应的行
在这里插入图片描述

import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F

# 目标：word_embedding
# 考虑source sentence和 target sentence
# 对原始数据长度进行填充操作，
# 最后不同长度的源句子和目标句子整合成同等长度的句子
# 构建序列，序列的字符以其在词表中的索引的形式表示

# 定义源句子的长度source_length,目标句子的长度 target_length
src_len = torch.Tensor([2, 4]).to(torch.int32)
tgt_len = torch.Tensor([4, 3]).to(torch.int32)

# 定义相关参数
# 批量大小
batch_size = 2

# 模型的特征大小
model_dim = 5

# 序列的最大长度
max_src_seq_len = 5
max_tgt_seq_len = 5

# 定义单词表的大小
max_num_src_words = 8
max_num_tgt_words = 8

# 1.将不同长度的源句子填充成统一长度/
# 2.将源句子张量按行堆叠起来
# src_seq 单词索引构成的句子

src_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_src_words, (L,)), (0, max_src_seq_len - L)), 0) for L in src_len], 0)
tgt_seq = torch.cat([torch.unsqueeze(F.pad(torch.randint(1, max_num_tgt_words, (L,)), (0, max_tgt_seq_len - L)), 0) for L in tgt_len], 0)
print(f"src_seq=\n{src_seq}")
print(f"tgt_seq=\n{tgt_seq}")

# 构造 word_Embedding;
# source_embedding和target_embedding
# 1.创建单词表；
# 2.通过序号去单词表中取出对应行数

src_embedding_table = nn.Embedding(max_num_src_words,model_dim)
tgt_embedding_table = nn.Embedding(max_num_tgt_words,model_dim)
print(f"src_embedding_table=\n{src_embedding_table.weight}")
print(f"tgt_embedding_table=\n{tgt_embedding_table.weight}")

# 通过src_seq的序号来从src_embedding_table中取出行数
src_embedding = src_embedding_table(src_seq)
# 通过tgt_seq的序号来从tgt_embedding_table中取出行数
tgt_embedding = tgt_embedding_table(tgt_seq)
print(f"src_embedding={src_embedding}")
print(f"tgt_embedding={tgt_embedding}")

2. position embedding

因为transformer模型既没有RNN也没有Conv卷积,为了使得模型具有顺序序列的信息，我们需要对模型进行顺序位置编码，按如下公式可得，对于奇数列和偶数列进行不同的位置编码，通过正余弦表示可以得到序列的绝对和相对位置信息；
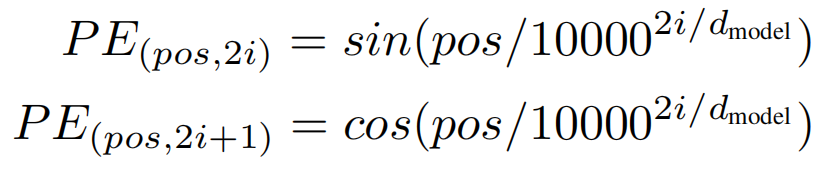
在这里插入图片描述

思路：

（1）创建一个pos_mat列向量表示pe_embedding_table的行

（2）创建一个i_mat行向量表示pe_embedding_table的列

（3）通过广播机制得到 $pos/10000^{2i/d_{model}}$

（4）创建一个全零的列表pe_embedding_table = torch.zeros(max_position_len, model_dim)

（5）将偶数列填充sin,奇数列填充cos；得到含值的pe_embedding_table

（6）实例化一个新的pe_embedding

（7）将pe_embedding.weight = pe_embedding_table

（8）完成

import torch
import torch.nn as nn
import numpy as np
import torch.nn.functional as F

# 目标：word_embedding
# 考虑source sentence和 target sentence
# 对原始数据长度进行填充操作，
# 最后不同长度的源句子和目标句子整合成同等长度的句子
# 构建序列，序列的字符以其在词表中的索引的形式表示

# 定义源句子的长度source_length,目标句子的长度 target_length
src_len = torch.Tensor([2, 4]).to(torch.int32)
tgt_len = torch.Tensor([4, 3]).to(torch.int32)

# 定义相关参数
# 批量大小
batch_size = 2

# 模型的特征大小
model_dim = 8

# 序列的最大长度
max_src_seq_len = 5
max_tgt_seq_len = 5
max_position_len = 5

# 定义单词表的大小
max_num_src_words = 8
max_num_tgt_words = 8

# 1.将不同长度的源句子填充成统一长度/
# 2.将源句子张量按行堆叠起来
# src_seq 单词索引构成的句子

src_seq = torch.cat(
	[torch.unsqueeze(F.pad(torch.randint(1, max_num_src_words, (L,)), (0, max_src_seq_len - L)), 0) for L in src_len],
	0)
tgt_seq = torch.cat(
	[torch.unsqueeze(F.pad(torch.randint(1, max_num_tgt_words, (L,)), (0, max_tgt_seq_len - L)), 0) for L in tgt_len],
	0)
print(f"src_seq=\n{src_seq}")
print(f"tgt_seq=\n{tgt_seq}")

# 构造 word_Embedding;
# source_embedding和target_embedding
# 1.创建单词表；
# 2.通过序号去单词表中取出对应行数

src_embedding_table = nn.Embedding(max_num_src_words, model_dim)
tgt_embedding_table = nn.Embedding(max_num_tgt_words, model_dim)
print(f"src_embedding_table=\n{src_embedding_table.weight}")
print(f"tgt_embedding_table=\n{tgt_embedding_table.weight}")

# 通过src_seq的序号来从src_embedding_table中取出行数
src_embedding = src_embedding_table(src_seq)
# 通过tgt_seq的序号来从tgt_embedding_table中取出行数
tgt_embedding = tgt_embedding_table(tgt_seq)
print(f"src_embedding={src_embedding}")
print(f"tgt_embedding={tgt_embedding}")

# 构造position_Embedding
pos_mat = torch.arange(max_position_len).reshape((-1, 1))
i_mat = torch.pow(10000, torch.arange(0, 8, 2).reshape((1, -1)) / model_dim)
pe_embedding_table = torch.zeros(max_position_len, model_dim)
print(f"pos_mat.shape={pos_mat.shape}")
print(f"pos_mat={pos_mat}")
print(f"i_mat.shape={i_mat.shape}")
print(f"i_mat={i_mat}")
print(f"pe_embedding_table.shape={pe_embedding_table.shape}")
pe_embedding_table[:, 0::2] = torch.sin(pos_mat / i_mat)
pe_embedding_table[:, 1::2] = torch.cos(pos_mat / i_mat)
print(f"pe_embedding_table={pe_embedding_table}")

# 实例化一个Embedding,并将我们定义的好的pe_embedding_table赋值实例化pe_embedding.weight
pe_embedding = nn.Embedding(max_position_len, model_dim)
pe_embedding.weight = nn.Parameter(pe_embedding_table, requires_grad=False)
print(f"pe_embedding_table={pe_embedding_table}")
print(f"pe_embedding.weight={pe_embedding.weight}")

# 通过字符的位置从单词表中获取
src_pos = torch.cat([torch.unsqueeze(torch.arange(max(src_len)),0)for _ in src_len],0)
tgt_pos = torch.cat([torch.unsqueeze(torch.arange(max(tgt_len)),0)for _ in tgt_len],0)
print(f"src_pos={src_pos}")
print(f"tgt_pos={tgt_pos}")
src_pe_embedding = pe_embedding(src_pos)
tgt_pe_embedding = pe_embedding(tgt_pos)
print(f"src_pe_embedding={src_pe_embedding}")
print(f"tgt_pe_embedding={tgt_pe_embedding}")

3. encoder self-attention mask

背景：
对于Encoder self-attention 来说我们希望没有数据的部分不参与梯度更新，也希望值经过softmax后概率就默认为0了。所以我们希望有一个encoder self-attention mask ，通过将部分padding填充的值赋值为负无穷，通过softmax后概率值为0；本质上是求得关系矩阵mask；
$f(x)=softmax(x_i)=\frac{e^{x_i}}{\sum_{i=1}^N e^{x_i}}$
$f(-inf)=softmax(-inf)=\frac{e^{-inf}}{e^{-inf}+C}=0$

3.1 softmax函数中值的大小对概率分布的影响

Scaled Dot-Product Attention:

为了进行有效的计算，我们需要将 $QK^T$ 除以一个值 $\sqrt{d_k}$ 使得模型更好的进行训练；

3.1.1 从概率分布角度分析

结论 :pro = softmax(Ax)中 x 越大，导致prob分布越不均匀，越不易训练；所以我们尽可能的要保证x越小；
prob1_alpha_0.1 = tensor([0.2304, 0.2011, 0.1842, 0.1787, 0.2057])- 概率分布均匀
prob2_alpha_10 = tensor([9.9999e-01, 1.2274e-06, 1.9065e-10, 9.5897e-12, 1.1844e-05])- 概率分布不均匀
代码：

# -*- coding: utf-8 -*-
# @Project: zc
# @Author: zc
# @File name: self_attetion_test
# @Create time: 2022/4/3 18:50

import torch
from torch import nn
from torch.nn import functional as F

score = torch.randn(5)
alpha1 = 0.1
alpha2 = 10
score_alpha1 = score * alpha1
score_alpha2 = score * alpha2
print(f"score={score}")
print(f"alpha1={alpha1}")
print(f"alpha2={alpha2}\n")
print(f"score_alpha1={score_alpha1}")
print(f"score_alpha2={score_alpha2}")
prob1 = F.softmax(score_alpha1,dim=0)
prob2 = F.softmax(score_alpha2,dim=0)

print(f"score\t=\t{score}\n")
print(f"prob1_alpha_0.1\t=\t{prob1}")
print(f"prob2_alpha_10 \t=\t{prob2}")

结论：

score=tensor([ 1.4681,  0.1070, -0.7700, -1.0689,  0.3337])
alpha1=0.1
alpha2=10

score_alpha1=tensor([ 0.1468,  0.0107, -0.0770, -0.1069,  0.0334])
score_alpha2=tensor([ 14.6809,   1.0703,  -7.6997, -10.6894,   3.3372])
score	=	tensor([ 1.4681,  0.1070, -0.7700, -1.0689,  0.3337])

prob1_alpha_0.1	=	tensor([0.2304, 0.2011, 0.1842, 0.1787, 0.2057])
prob2_alpha_10 	=	tensor([9.9999e-01, 1.2274e-06, 1.9065e-10, 9.5897e-12, 1.1844e-05])

3.1.2 从雅克比角度分析

结论 :pro = softmax(Ax)中 x 越大，导致jacobian越小，从而越不易训练；所以我们尽可能的要保证x越小；

# -*- coding: utf-8 -*-
# @Project: zc
# @Author: zc
# @File name: self_attetion_test
# @Create time: 2022/4/3 18:50

import torch
from torch import nn
from torch.nn import functional as F

score = torch.randn(5)
alpha1 = 0.1
alpha2 = 10
score_alpha1 = score * alpha1
score_alpha2 = score * alpha2

def softmax_fun(x):
	return F.softmax(x)


jacobian_alpha_1 = torch.autograd.functional.jacobian(softmax_fun, score_alpha1)
jacobian_alpha_2 = torch.autograd.functional.jacobian(softmax_fun, score_alpha2)

print(f"jacobian_alpha_0.1={jacobian_alpha_1}")
print(f"jacobian_alpha_10 ={jacobian_alpha_2}")

结果


# 当 alpha=0.1时候，jacobian_alpha_0.1分布合理，模型可以有效的更新参数

jacobian_alpha_0.1=tensor([[ 0.1506, -0.0376, -0.0372, -0.0425, -0.0333],
        [-0.0376,  0.1620, -0.0409, -0.0468, -0.0367],
        [-0.0372, -0.0409,  0.1607, -0.0463, -0.0363],
        [-0.0425, -0.0468, -0.0463,  0.1772, -0.0415],
        [-0.0333, -0.0367, -0.0363, -0.0415,  0.1479]])


# 当 alpha=10 时候，jacobian_alpha_10 分布不合理，值太小，模型不能有效的更新参数

jacobian_alpha_10 =tensor([[ 2.8146e-10, -1.2089e-15, -3.9558e-16, -2.8145e-10, -7.7739e-21],
        [-1.2089e-15,  4.2950e-06, -6.0366e-12, -4.2950e-06, -1.1863e-16],
        [-3.9558e-16, -6.0366e-12,  1.4055e-06, -1.4055e-06, -3.8820e-17],
        [-2.8145e-10, -4.2950e-06, -1.4055e-06,  5.7220e-06, -2.7620e-11],
        [-7.7739e-21, -1.1863e-16, -3.8820e-17, -2.7620e-11,  2.7620e-11]])

3.2 Scaled-Dot-Product Attention

Scaled Dot-Product Attention 公式形式
Scaled-Dot-Product-Attention 和Multi-Head-Attention的关系
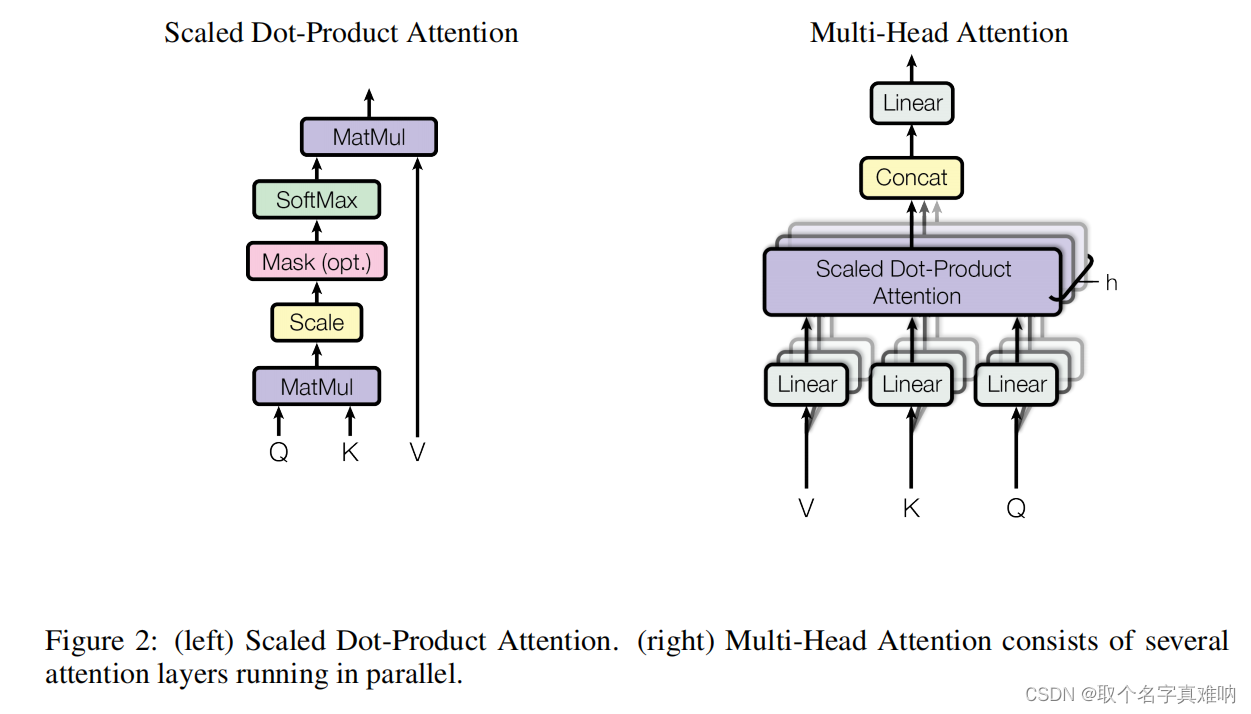
临接矩阵；计算样本两两矩阵的相关性
假设源句子的长度为src_len=torch.Tensor([2,4])，我们要得到一组mask矩阵，其作用是通过mask来表示关联性；

# 假设我们源句子的数据第一个样本有2个，第二个样本有4个
src_len=tensor([2, 4], dtype=torch.int32)
# 1.根据长度得到全1矩阵[1,1],[1,1,1,1]
# 2.根据max(src_len)得到填充矩阵[1,1,0,0],[1,1,1,1]
# 3.将[1,1,0,0]中每个单词拿出来跟其他单词进行比较，第一个1单词只跟本身和第二个单词有关，与其他无关
# 4. 所以第一个样本得到的结果为：
#        [[1., 1., 0., 0.],
#         [1., 1., 0., 0.],
#         [0., 0., 0., 0.],
#         [0., 0., 0., 0.]]
# 5.同理[1,1,1,1]都有值，都相关，所以全为1，结果如下：
#         [[1., 1., 1., 1.],
#          [1., 1., 1., 1.],
#          [1., 1., 1., 1.],
#          [1., 1., 1., 1.]]
valid_encoder_pos_matrix=
tensor([[[1., 1., 0., 0.],
         [1., 1., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])

代码

import torch
from torch import nn
from torch.nn import functional as F
import numpy as np

src_len = torch.Tensor([2, 4]).to(torch.int32)
tgt_len = torch.Tensor([3, 2]).to(torch.int32)

max_src_seq_len = 5
max_tgt_seq_len = 5
batch_size =2
# 构造一个encoder的self-attention的mask
# mask的shape：[batch_size,max_src_len,max_src_len]值为1或-inf负无穷

# valid_encoder_pos.shape=torch.Size([batch_size=2,1,max_src_len=4])
valid_encoder_pos = torch.unsqueeze(torch.cat([torch.unsqueeze(F.pad(torch.ones(L), (0, max(src_len) - L)), 0)
											   for L in src_len], 0), 2)

# 临接矩阵(2,4,4) = torch.bmm[(2,1,4),(2,4,1)]
# 表示每一个值A关于同行值B的关联性
valid_encoder_pos_matrix = torch.bmm(valid_encoder_pos, valid_encoder_pos.transpose(-1, -2))

print(f"valid_encoder_pos.shape={valid_encoder_pos.shape}")
print(f"valid_encoder_pos.transpose(-1,-2).shape={valid_encoder_pos.transpose(-1, -2).shape}")
print(f"valid_encoder_pos_matrix.shape={valid_encoder_pos_matrix.shape}")
print(f"src_len={src_len}")
invalid_encoder_pos_matrix = (1 - valid_encoder_pos_matrix)
# 得到mask的矩阵，通过mask矩阵的True可以看到哪些是填充的
mask_encoder_self_attention = invalid_encoder_pos_matrix.to(torch.bool)

print(f"valid_encoder_pos_matrix=\n{valid_encoder_pos_matrix}")
print(f"invalid_encoder_pos_matrix=\n{invalid_encoder_pos_matrix}")
print(f"mask_encoder_self_attention={mask_encoder_self_attention}")


score = torch.randn(batch_size,max(src_len),max(src_len))

# 将score里面的值，如果mask_encoder_self_attention里面值为True的赋值为负无穷或非常小的值
masked_score = score.masked_fill(mask_encoder_self_attention,-1e09)
prob = F.softmax(masked_score,-1)
print(f"score={score}")
print(f"masked_score={masked_score}")
print(f"prob={prob}")

结果：

valid_encoder_pos.shape=torch.Size([2, 4, 1])
valid_encoder_pos.transpose(-1,-2).shape=torch.Size([2, 1, 4])
valid_encoder_pos_matrix.shape=torch.Size([2, 4, 4])
src_len=tensor([2, 4], dtype=torch.int32)
valid_encoder_pos_matrix=
tensor([[[1., 1., 0., 0.],
         [1., 1., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]],

        [[1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]]])
invalid_encoder_pos_matrix=
tensor([[[0., 0., 1., 1.],
         [0., 0., 1., 1.],
         [1., 1., 1., 1.],
         [1., 1., 1., 1.]],

        [[0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.],
         [0., 0., 0., 0.]]])
mask_encoder_self_attention=tensor([[[False, False,  True,  True],
         [False, False,  True,  True],
         [ True,  True,  True,  True],
         [ True,  True,  True,  True]],

        [[False, False, False, False],
         [False, False, False, False],
         [False, False, False, False],
         [False, False, False, False]]])
score=tensor([[[-0.7478,  0.3740,  1.6095,  0.8876],
         [-0.0135,  1.1454, -2.0284, -0.4761],
         [ 0.4100, -0.0771,  1.1361, -2.2469],
         [-0.2719,  1.8155,  0.3797, -0.9952]],

        [[ 0.7262,  2.1460, -1.1438,  1.0181],
         [ 0.8990,  0.2356, -0.1258, -0.2997],
         [-0.1403,  0.9309,  0.6472, -1.1315],
         [ 0.2317, -1.0411, -2.2385,  0.6930]]])
masked_score=tensor([[[-7.4780e-01,  3.7398e-01, -1.0000e+09, -1.0000e+09],
         [-1.3502e-02,  1.1454e+00, -1.0000e+09, -1.0000e+09],
         [-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09],
         [-1.0000e+09, -1.0000e+09, -1.0000e+09, -1.0000e+09]],

        [[ 7.2624e-01,  2.1460e+00, -1.1438e+00,  1.0181e+00],
         [ 8.9903e-01,  2.3565e-01, -1.2584e-01, -2.9972e-01],
         [-1.4031e-01,  9.3090e-01,  6.4719e-01, -1.1315e+00],
         [ 2.3167e-01, -1.0411e+00, -2.2385e+00,  6.9296e-01]]])
prob=tensor([[[0.2457, 0.7543, 0.0000, 0.0000],
         [0.2389, 0.7611, 0.0000, 0.0000],
         [0.2500, 0.2500, 0.2500, 0.2500],
         [0.2500, 0.2500, 0.2500, 0.2500]],

        [[0.1508, 0.6239, 0.0232, 0.2020],
         [0.4597, 0.2368, 0.1649, 0.1386],
         [0.1541, 0.4499, 0.3388, 0.0572],
         [0.3389, 0.0949, 0.0287, 0.5375]]])