1.目标及步骤
- 步骤1:网上搜索实证网络;
- 步骤2:将收集的实证网络可视化(工具推荐:python+networkx);
- 步骤3:计算所收集到的网络性质(包括:度分布,聚类系数,网络直径,度关联性,权重分析)
- 步骤4: 分析
数据集说明:本项目数据源自2021年美赛数学建模D题所给予数据集的influence_data.csv。【 因为这个项目的目标是实证网络,所以我选取了其中的一份数据,这是一份42770*8的数据,,此数据描述的是一定时期内,各个音乐流派中的音乐家的追随关系,由于音乐家的追随方向实际上是影响一个音乐流派的发展方向,对此我们可以搭建网络探究各个音乐流派之间发展的影响】

2.理论基础 - 网络性质
2.1度分布
2.1.1性质
度(degree)是指网络(图)中一个点的与其他点的连接数量,度分布(Degree Distribution)就是整个网络中,各个点的度数量的概率分布。例如: 度分布P(k)是指,网络中度为k的节点的出现概率;对于有向图来说又分为入度分布和出度分布。如果网络中总共有n个节点,其中有nk个度为k的节点,那么
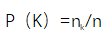
定义P(k)为网络中度为k的节点在整个网络中所占的比率
2.1.2数值/结果分析
- 规则网络:由于每个节点具有相同的度,所以其度分布集中在一个单一尖峰上,是一种Delta分布。
- 完全随机网络:度分布具有Poisson分布的形式,每一条边的出现概率是相等的,大多数节点的度是基本相同的,并接近于网络平均度<k>,远离峰值<k>,度分布则按指数形式急剧下降。把这类网络称为均匀网络
- 无标度网络:具有幂指数形式的度分布:P(k)∝k?γ 。 ?指数度分布网络: P(k)∝e?k/к,式中к>0为一常数

2.1.3代码
import matplotlib.pyplot as plt # 导入科学绘图包
import networkx as nx
import numpy as np
adj = np.loadtxt('adj.txt', dtype=np.int) # 邻接矩阵
G = nx.from_numpy_matrix(adj) # 网络图
degree = nx.degree_histogram(G) # 返回图中所有节点的度分布序列【核心】
x = range(len(degree)) # 生成X轴序列,从1到最大度
y = [z / float(sum(degree)) for z in degree] # 将频次转化为频率
plt.ylabel("Frequency", size=14) # Frequency
plt.xticks(fontproperties='Times New Roman', size=13)
plt.yticks(fontproperties='Times New Roman', size=13)
plt.loglog(x, y, '.')
plt.show() # 显示图表
2.2聚类系数
2.2.1性质 - 无向网络
假设节点vi与ki个节点直接连接,那么对于无向网络来说,这ki个节点间可能存在的最大边数为ki(ki-1)/2,而实际存在的边数为Mi,由此我们定义节点vi的集聚系数为
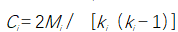
2.2.2性质 - 有向网络
对于有向网络来说,这ki个节点间可能存在的最大弧数为ki(ki-1),此时vi的集聚系数为
![Ci=Mi/[ki(ki-1)]](https://img-blog.csdnimg.cn/70cba1b440b74d6fa19e8aa84d2c062e.png)
将该集聚系数对整个网络作平均,可得网络的平均集聚系数为
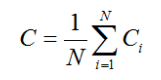
2.2.3结果分析
显然,0≤C≤1。
C=0:所有节点都是孤立节点,没有边连接。
C=1:网络为所有节点两两之间都有边连接的完全图
2.2.4代码
# cluster = nx.clustering(G)
# print("网络节点聚类系数为:", cluster)
# cluster = nx.clustering(G)
2.3网络直径
2.3.1性质
网络直径:网络的直径D定义为所有距离dij中的最大值,指网络中任意两个节点间距离的最大值,一般用链路数来度量,即
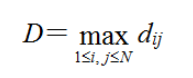
2.3.2代码
# nx.diameter(G)
2.4度关联性
2.4.1性质
度中心性分为节点度中心性和网络度中心性。前者指的是节点在其与之直接相连的邻居节点当中的中心程度,而后者则侧重节点在整个网络的中心程度,表征的是整个网络的集中或集权程度,即整个网络围绕一个节点或一组节点来组织运行的程度。节点vi的度中心性CD(vi)定义为
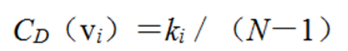
在所有含N节点的网络中,假设网络Goptimal使得下式达到最大值
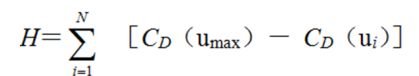
式中,ui为网络Goptimal的各个节点,u max表示网络Goptimal中拥有最大度中心性的节点
2.4.2结果分析
是整个网络的集中或集权程度,即整个网络围绕一个节点或一组节点来组织运行的程度
2.4.3代码
# nx.degree_centrality(G)
3.实证网络过程
3.1数据来源
本项目数据源自2021年美赛数学建模D题所给予数据集的influence_data.csv,此数据描述的是一定时期内,各个音乐流派中的音乐家的追随关系,由于音乐家的追随方向实际上是影响一个音乐流派的发展方向,对此我们可以搭建网络探究各个音乐流派之间发展的影响。流派数据大小为42771*8(42771含列名influencer_id、influencer_name、influencer_main_genre、influencer_active_start、follower_id、follower_name、follower_main_genre、follower_active_start)
表1 字段描述
字段名称 字段类型 字段说明
influencer_id 整型 影响者唯一编号
influencer_name 字符型 影响者音乐家姓名
influencer_main_genre 字符型 影响者所在流派
influencer_active_start 字符型 影响者出道时间
follower_id 整型 追随者唯一编号
follower_name 字符型 追随者音乐家姓名
follower_main_genre 字符型 追随者所在流派
follower_active_start 字符型 追随者出道时间
3.2数据处理
3.2.1获取音乐流派类型
获取音乐流派类型作为网络节点,创建数组k用来存储音乐类型,挨行遍历42770行,如果是k数组中没有的音乐流派数据类型,就追加数组,否则就舍弃,从而达到获取不同的音乐类型效果
代码👇

为避免后续每运行一次代码都跑一边类型,所以存储音乐流派类型👇
3.2.2无向图绘制
网络的初步搭建,依据音乐流派类型作为节点,循环遍历每个节点作为边
代码👇
结果 👇
*
3.2.3获取有向边权重
创建全零的二维数组weight,当我判断每一行的键是由哪两个流派所影响存在时,进行权重的累计并存储,其中可利用excel进行验证
代码👇

结果👇

验证👇

存储后的权重读取代码👇
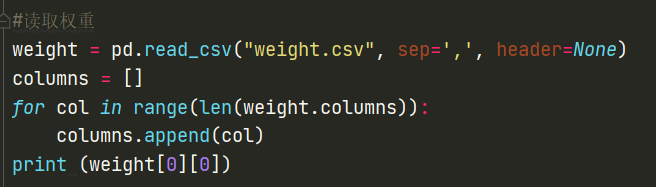
3.2.4绘制有向图
根据节点、权重可视化绘制有向图
代码👇
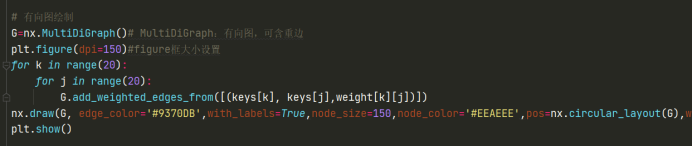
结果👇

3.3指标分析
3.3.1度分布
由于本实证网络是有向完全图,是符合规则网络【由于每个节点具有相同的度,所以其度分布集中在一个单一尖峰上,是一种Delta分布】
代码👇

结果👇


3.3.2网络直径
指网络中任意两个节点间距离的最大值,一般用链路数来度量,因为是完全图,所以每两个节点都相连,所以网络直径为1
代码👇

结果👇
3.3.3度中心性
每一个节点的度中心性均相等
代码👇

结果👇

3.3.4度聚类系数
C=1:网络为所有节点两两之间都有边连接的完全图
代码👇
结果👇
3.3.5权重以及入度分析
线越宽代表联系越紧密,点越大表示出现的次数越多
代码👇

结果👇

Pop/rock影响力大 Pop/Rock与R&B强关联
4.完整代码
import networkx as nx
import matplotlib.pyplot as plt
import numpy as np
import pandas as pd
file = "influence_data.csv"
influence=pd.read_csv(file,sep=',',encoding='utf-8')
influencer_genre=influence['influencer_main_genre'].values
# print(influencer_genre.shape[0])#42770
follower_genre=influence['follower_main_genre'].values
# # 得到csv中音乐流派类型
# k=[0]
# for i in range(influencer_genre.shape[0]-1):
# if influencer_genre[i]!=influencer_genre[i+1]:
# for j in range(len(k)):
# if influencer_genre[i+1]!=k[j]:
# k.append(influencer_genre[i+1])
# print(k)
dict={'Pop/Rock':0,'Country':0,'Classical':0,'Electronic':0,'Comedy/Spoken':0,'Easy Listening':0,'R&B;':0,'Stage & Screen':0,'Reggae':0,'Blues':0,'New Age':0,'Latin':0,'Vocal':0,'Jazz':0,'International':0,'Folk':0,'Religious':0,'Unknown':0,'Avant-Garde':0,'Children\'s':0}
keys=list(dict.keys())
# # 获取有向权重【流派之间的指向】
# dict_class={}
# dict_class_keys=list(dict_class.keys())
# weight =np.zeros((20, 20))
# for n in range(influencer_genre.shape[0]-1):
# for k in range(20):
# for j in range(20):
# if ((influencer_genre[n]==keys[k]) &(follower_genre[n]==keys[j]) ):
# weight[j][k] = weight[j][k] + 1
# dict_class[keys[k] + '-' + keys[j]] = weight[j][k]
#
# print(dict_class)#{'Pop/Rock-Pop/Rock': 22049.0, 'Electronic-Pop/Rock': 297.0, 'Reggae-Pop/Rock': 166.0, 'Jazz-Pop/Rock': 409.0, 'Country-Pop/Rock': 641.0, 'Comedy/Spoken-Pop/Rock': 33.0, 'R&B;-Pop/Rock': 1625.0, 'Country-Country': 2502.0, 'Classical-Classical': 17.0, 'Latin-Electronic': 7.0, 'Vocal-Comedy/Spoken': 4.0, 'Comedy/Spoken-Comedy/Spoken': 101.0, 'Folk-Comedy/Spoken': 5.0, 'Pop/Rock-Easy Listening': 9.0, 'Easy Listening-Easy Listening': 18.0, 'Latin-Easy Listening': 5.0, 'International-Easy Listening': 2.0, 'Vocal-Easy Listening': 2.0, 'Classical-Electronic': 16.0, 'Pop/Rock-Electronic': 504.0, 'Jazz-Electronic': 46.0, 'Avant-Garde-Electronic': 17.0, 'R&B;-R&B;': 3384.0, 'Blues-Pop/Rock': 689.0, 'Classical-Stage & Screen': 5.0, 'Stage & Screen-Stage & Screen': 80.0, 'Pop/Rock-Stage & Screen': 10.0, 'Reggae-Reggae': 584.0, 'Jazz-Blues': 33.0, 'New Age-New Age': 47.0, 'Jazz-R&B;': 176.0, 'Pop/Rock-Latin': 132.0, 'Latin-Latin': 405.0, 'R&B;-Latin': 31.0, 'Vocal-R&B;': 231.0, 'Pop/Rock-R&B;': 284.0, 'Classical-Pop/Rock': 43.0, 'Stage & Screen-Pop/Rock': 51.0, 'Vocal-Vocal': 537.0, 'Pop/Rock-Vocal': 75.0, 'Jazz-Vocal': 105.0, 'Jazz-Jazz': 1769.0, 'International-Jazz': 20.0, 'Electronic-Electronic': 372.0, 'Stage & Screen-Vocal': 23.0, 'R&B;-International': 11.0, 'Blues-International': 5.0, 'Blues-R&B;': 118.0, 'Vocal-Pop/Rock': 381.0, 'Folk-Pop/Rock': 553.0, 'Latin-Pop/Rock': 103.0, 'Pop/Rock-Country': 519.0, 'Blues-Jazz': 17.0, 'Comedy/Spoken-Country': 2.0, 'Blues-Blues': 372.0, 'Pop/Rock-Blues': 47.0, 'Pop/Rock-Jazz': 95.0, 'Religious-R&B;': 40.0, 'Pop/Rock-Comedy/Spoken': 30.0, 'R&B;-Comedy/Spoken': 4.0, 'R&B;-Jazz': 71.0, 'Electronic-New Age': 26.0, 'Pop/Rock-New Age': 37.0, 'Avant-Garde-New Age': 7.0, 'Folk-Folk': 271.0, 'Jazz-Religious': 2.0, 'Blues-Religious': 1.0, 'Vocal-Religious': 9.0, 'Pop/Rock-Folk': 166.0, 'International-Folk': 11.0, 'Latin-Jazz': 37.0, 'Religious-Religious': 155.0, 'Vocal-Country': 36.0, 'International-Pop/Rock': 116.0, 'Stage & Screen-Classical': 1.0, 'Pop/Rock-Classical': 25.0, 'New Age-Classical': 3.0, 'Electronic-Classical': 1.0, 'Religious-Pop/Rock': 37.0, 'Stage & Screen-Electronic': 12.0, 'New Age-Jazz': 5.0, 'Easy Listening-Pop/Rock': 31.0, 'Folk-Country': 108.0, 'Blues-Country': 6.0, 'Latin-R&B;': 8.0, 'New Age-Pop/Rock': 18.0, 'Comedy/Spoken-Folk': 5.0, 'Vocal-Folk': 16.0, 'Jazz-Country': 24.0, 'Pop/Rock-Reggae': 24.0, 'R&B;-Country': 39.0, 'Easy Listening-Jazz': 8.0, 'R&B;-Electronic': 88.0, 'R&B;-Blues': 50.0, 'Folk-Blues': 3.0, 'Blues-Electronic': 1.0, 'International-Electronic': 5.0, 'Pop/Rock-Religious': 83.0, 'Country-Religious': 6.0, 'Vocal-Electronic': 2.0, 'Reggae-Electronic': 34.0, 'Pop/Rock-International': 37.0, 'Avant-Garde-Pop/Rock': 42.0, 'R&B;-Religious': 74.0, 'Folk-R&B;': 8.0, 'R&B;-Reggae': 104.0, 'Easy Listening-Vocal': 4.0, 'Jazz-Classical': 5.0, 'Vocal-Jazz': 84.0, 'Country-Folk': 101.0, 'Reggae-R&B;': 8.0, 'International-Classical': 5.0, 'Folk-Latin': 1.0, 'Easy Listening-New Age': 5.0, 'Jazz-New Age': 28.0, 'Folk-Religious': 7.0, 'International-Religious': 1.0, 'Blues-Folk': 24.0, 'Jazz-Folk': 11.0, 'Country-International': 3.0, 'Vocal-Stage & Screen': 8.0, 'Country-R&B;': 7.0, 'Latin-Vocal': 8.0, 'International-Vocal': 10.0, 'Vocal-Classical': 15.0, 'R&B;-Classical': 2.0, 'Folk-Classical': 1.0, 'Vocal-Latin': 45.0, 'R&B;-Vocal': 38.0, 'International-International': 81.0, 'Jazz-International': 22.0, 'Latin-International': 41.0, 'Jazz-Comedy/Spoken': 5.0, 'Classical-Vocal': 10.0, 'Country-Jazz': 11.0, 'Religious-Vocal': 4.0, 'Folk-Vocal': 3.0, 'Vocal-Blues': 15.0, 'Folk-New Age': 17.0, 'International-Reggae': 11.0, 'Jazz-Reggae': 11.0, 'Vocal-International': 22.0, 'Folk-International': 29.0, 'Latin-Religious': 1.0, 'Stage & Screen-Jazz': 6.0, 'Comedy/Spoken-Vocal': 3.0, 'International-Latin': 37.0, 'Jazz-Latin': 41.0, 'Easy Listening-Latin': 3.0, 'Country-Unknown': 3.0, 'Pop/Rock-Unknown': 4.0, 'Electronic-R&B;': 12.0, 'International-New Age': 12.0, 'R&B;-New Age': 1.0, 'Country-Vocal': 7.0, 'New Age-Electronic': 10.0, 'Easy Listening-Stage & Screen': 5.0, 'New Age-Latin': 1.0, 'Religious-Country': 8.0, 'R&B;-Folk': 6.0, 'Reggae-Latin': 10.0, 'Vocal-New Age': 1.0, 'Classical-New Age': 4.0, 'Blues-Latin': 1.0, 'Country-Latin': 2.0, 'Classical-Avant-Garde': 11.0, 'Avant-Garde-Avant-Garde': 7.0, 'International-Avant-Garde': 2.0, 'Jazz-Avant-Garde': 2.0, 'Vocal-Reggae': 5.0, 'Country-Reggae': 1.0, 'Blues-Vocal': 5.0, 'Country-Blues': 10.0, 'Comedy/Spoken-R&B;': 4.0, 'Country-Comedy/Spoken': 1.0, 'New Age-Folk': 2.0, 'International-R&B;': 12.0, 'Jazz-Easy Listening': 12.0, 'Comedy/Spoken-Electronic': 1.0, 'Reggae-International': 2.0, 'New Age-International': 2.0, 'New Age-Vocal': 3.0, 'Jazz-Stage & Screen': 14.0, 'Stage & Screen-Folk': 2.0, 'Religious-Folk': 3.0, 'Latin-New Age': 3.0, 'International-Blues': 1.0, 'Classical-Country': 2.0, "Children's-Pop/Rock": 1.0, 'Latin-Country': 1.0, 'Easy Listening-Avant-Garde': 1.0, 'R&B;-Avant-Garde': 2.0, 'Pop/Rock-Avant-Garde': 11.0, 'Folk-Electronic': 3.0, 'Classical-International': 2.0, 'Stage & Screen-Country': 1.0, 'Comedy/Spoken-Stage & Screen': 1.0, 'Stage & Screen-International': 1.0, 'Classical-Jazz': 2.0, 'International-Unknown': 2.0, 'Easy Listening-International': 1.0, 'Stage & Screen-Easy Listening': 4.0, 'Classical-Easy Listening': 1.0, "Comedy/Spoken-Children's": 1.0, "Jazz-Children's": 1.0, 'Avant-Garde-Classical': 5.0, 'Latin-Classical': 1.0, "Children's-Children's": 2.0, 'Blues-Reggae': 3.0, 'Comedy/Spoken-Reggae': 1.0, 'Classical-Latin': 1.0, 'Folk-Jazz': 1.0, "Stage & Screen-Children's": 1.0, "Vocal-Children's": 1.0, 'Unknown-International': 1.0, 'New Age-Stage & Screen': 2.0, 'Country-New Age': 4.0, 'Country-Electronic': 2.0, 'Avant-Garde-Stage & Screen': 1.0, 'Latin-Stage & Screen': 1.0, 'Electronic-Stage & Screen': 1.0, 'Blues-New Age': 1.0, 'Reggae-Vocal': 1.0, 'Unknown-Pop/Rock': 1.0, 'Stage & Screen-Avant-Garde': 1.0, 'Electronic-Latin': 1.0, 'New Age-Easy Listening': 1.0}
#将权重存入‘weight.csv’
# np.savetxt("weight.csv", weight, delimiter=",")
#读取权重
weight = pd.read_csv("weight.csv", sep=',', header=None)
columns = []
for col in range(len(weight.columns)):
columns.append(col)
print (weight[0][0])
weight_plus=np.zeros([20])
# 有向图绘制
G=nx.MultiDiGraph()# MultiDiGraph:有向图,可含重边
plt.figure(dpi=150)#figure框大小设置
for k in range(20):
for j in range(20):
G.add_weighted_edges_from([(keys[k], keys[j],weight[k][j])])
# print(G.degree())
for n in range(20):
for i in range(20):
weight_plus[n] = weight[n][n]+weight[n][i]
line = '#EEAEEE #EEAEEE 0.8 0.8 0.8 0.8 #EEAEEE 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8 0.8' # 读取颜色向量
colors = (line.split(' ')) # 颜色向量
nx.draw(G, edge_color='#9370DB',node_color=colors,with_labels=True,pos=nx.circular_layout(G),
node_size=[v*0.1 for v in weight_plus],
width=[float(v['weight']/200) for (r, c, v) in G.edges(data=True)])
plt.show()
# # 度分布
# degree=nx.degree_histogram(G)
# print(degree)
# x=range(len(degree))
# y=[z/float(sum(degree))for z in degree]
# plt.loglog(x,y,color="blue",linewidth=2)
# plt.show()
#
# 网络直径
# 网络直径是指网络中任意两个节点间距离的最大值,一般用链路数来度量
print(nx.diameter(G))
# 度中心性
print(nx.degree_centrality(G))
# # 度聚类系数
# cluster = nx.clustering(G)
# print("网络节点聚类系数为:", cluster)