一.引言
多重信号分类(MUSIC)算法是 Schmidt RO等人在 1979 年提出的。这一算法的提出开创了空间谱估计算法研究的新时代,促进了特征结构类算法的兴起和发展,该算法已成为空间谱估计理论体系中的标志性算法。MUSIC算法的基本思想则是将任意阵列输出数据的协方差矩阵进行特征分解,从而得到与信号分量相对应的信号子空间和与信号分量相正交的噪声子空间,然后利用这两个子空间的正交性来估计信号的参数(入射方向、极化信息及信号强度等)。
下面简单推导一下MUSIC算法。
二.推导过程
窄带远场信号的DOA数学模型为(这部分内容读者可以参考有关阵列信号处理方面的书籍资料)
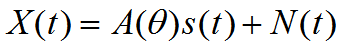
阵列数据的协方差矩阵为
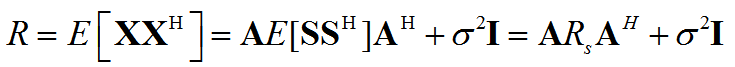
由于信号与噪声相互独立,数据协方差矩阵可分解为与信号、噪声相关的两部分,其中Rs是信号的协方差矩阵,ARsAH是信号部分。
对R进行特征分解有
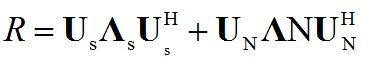
式中,Us是由大特征值对应的特征矢量张成的子空间也即信号子空间,而Un是由小特征值对应的特征矢量张成的子空间也即噪声子空间。
根据阵列模型的性质,理想条件下数据空间中的信号子空间与噪声子空间是相互正交的,即信号子空间中的导向矢量也与噪声子空间正交。
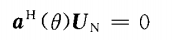
经典的 MUSIC算法正是基于上述这个性质提出的,但考虑到实际接收数据矩阵是有限长的,即数据协方差矩阵的最大似然估计为
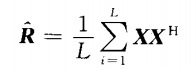
对R进行特征分解可以计算得到噪声子空间特征矢量矩阵Un。由于噪声的存在,a(0)与Un并不能完全正交。因此,实际上求DOA是以最小优化搜索实现的,即
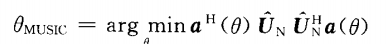
所以,MUSIC算法的谱估计公式为
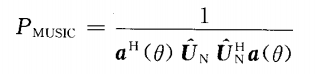
三.MUSIC算法详细步骤
1.由阵列的接收数据得到数据协方差矩阵R,即
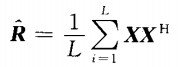
2.对R进行特征分解;
3.由R的特征值进行信号源数判断;
4.确定信号子空间Us与噪声子空间U、;
5.根据信号参数范围由
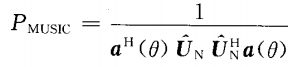
进行谱峰搜索;
6.找出极大值点对应的角度就是信号入射方向。
虽然波束空间算法的估计方差比阵元空间算法的要差,但波束空间算法存在如下优点∶一是计算量较低;二是提高了阵元空间谱估计算法的稳健性和鲁棒性;三是降低了系统的复杂性。某些波束空间算法比阵元空间算法具有更低的分辨力门限和估计偏差。
参考文献
[1] Schmidt RO. Multiple emitter location and signal parameter estimation.IEEE Trans. on AP,1986,34(3):276~280
[2] Stoica P,Nehorai A. MUSIC,maximum likelihood,and Cramer-Rao bound.IEEE Trans.on ASSP,1989,37(5); 720~741
[3] 王永良, 陈辉, 彭应宁, 万群, 空间谱估计理论与方法, 清华大学出版社, 2004.