[人工智能]机器学习_wed_01

1 线性回归

2.8 作业_01_线性回归

线性回归链接

6 逻辑回归

6.1 分类问题

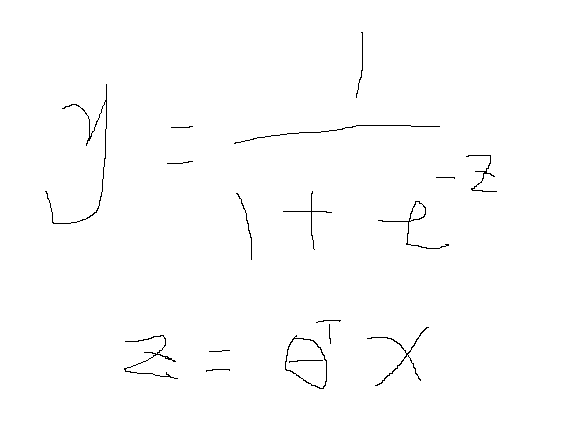
通过上面这个取值在[0，1]的函数，曲线类似arctan x进行拟合，通过数据计算出thyta向量值，然后让Z>0,解出x的范围如下图

6.3 决策边界

(thyda向量-3，1，1.)

6.4 代价函数

逻辑回归的代价函数不能使用之前的线性回归那样的平方做差之后当代价函数了，因为逻辑回归的待拟合的函数复杂，使用平方误差的方式写出来的代价函数是非凸的，有很多的局部最优解，不能使用梯度下降法解除全局最优解，如下图

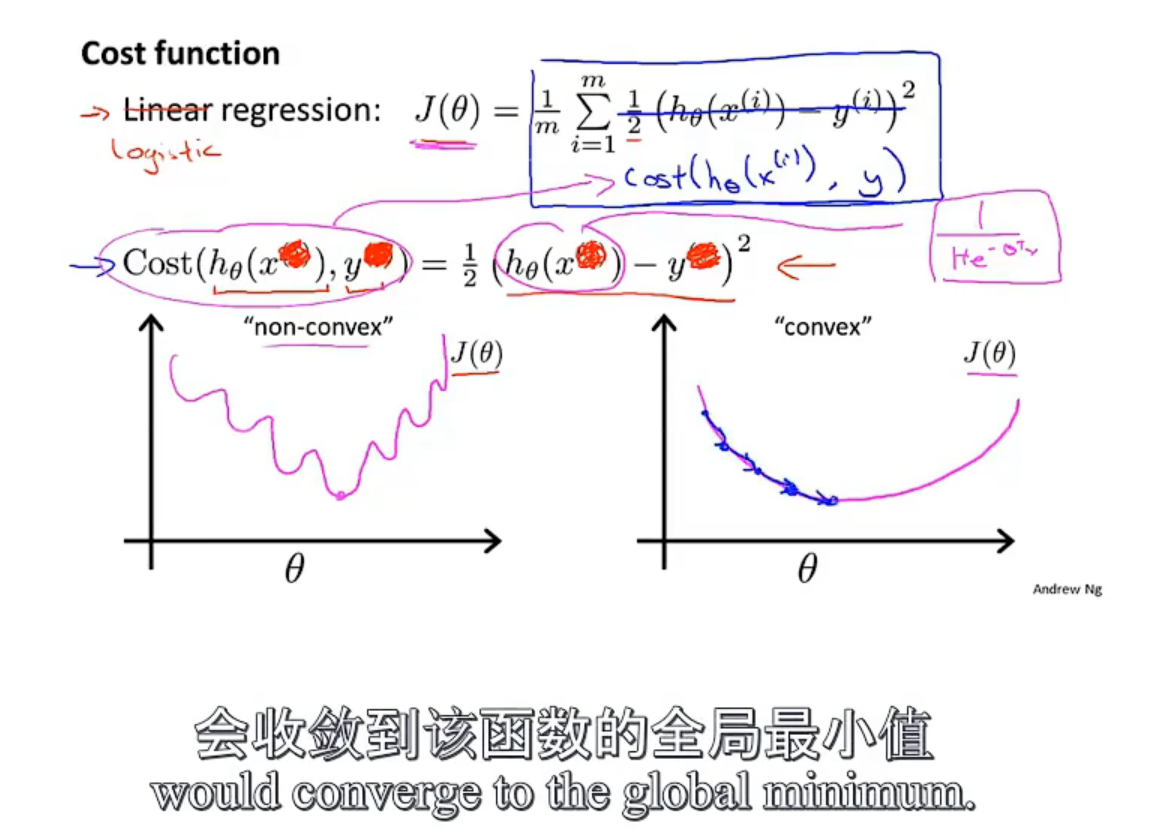
使用新的代价函数，如下图：

下边这个

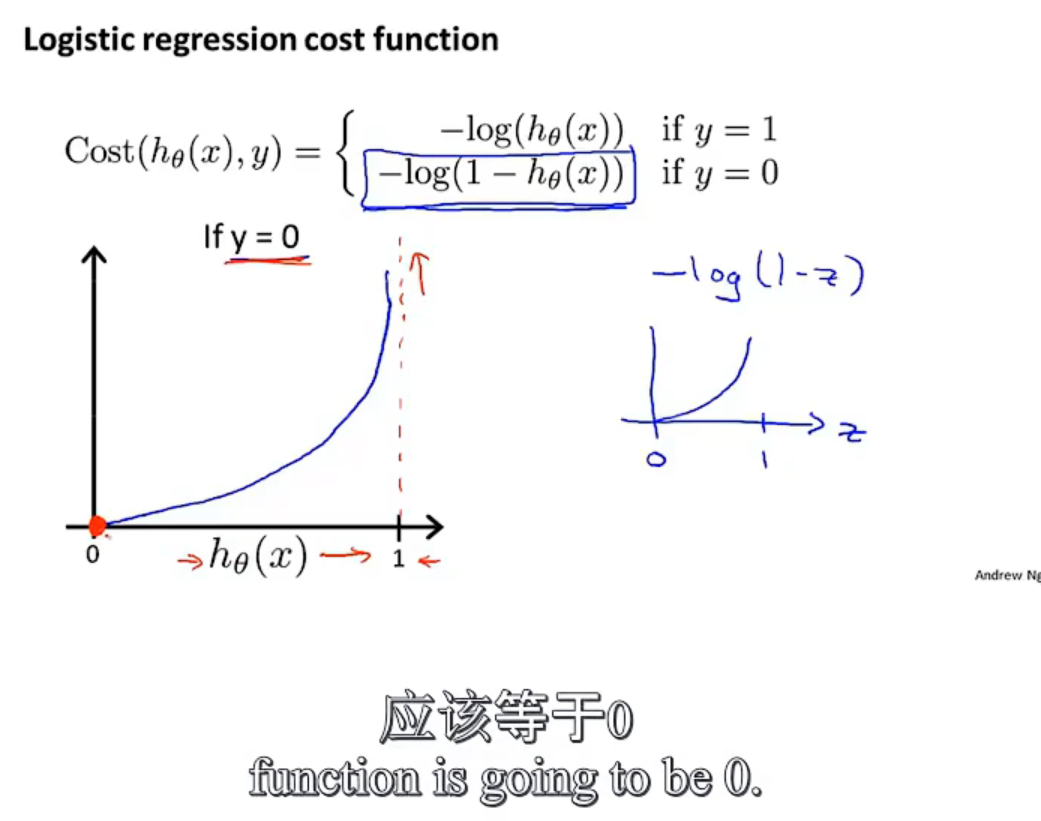
6.5 简化代价函数与梯度下降

使用一个式子代表逻辑回归的代价函数

然后执行梯度下降，每一个theta的更新都是当前值减去学习率 * 偏导项，虽然更新的式子是一样的，但是表达的是不一样的，因为原来的线性回归和逻辑回归的假设函数是不一样的，如下图所示：

6.6 高级优化

• gradient descent
• conjugate gradient
• BFGS
• L-BFGS
  相应语言有相应的高级算法的库，自己需要写一个适配的函数，来调用这个库里的函数。

6.7 多分类

多分几次

6.8 作业

参考

自己github链接

7 过拟合

7.1 过拟合

• 减少特征变量
• 正则化

7.2 代价函数

为了防止过拟合项，会通过增加惩罚项来减少各个特征的属性，修改之后的代价函数如下：

7.3 线性回归正则化

1、使用梯度下降求解

2、当使用矩阵求解时，通过正则化，可以使得中间产生的那个矩阵一定是可逆的。

7.4 逻辑回归的正则化

总结：
学了线性回归
学了逻辑回归
学了高级算法
学了正则化

8 非线性假设