具体来说,给定节点特征 H ( l ) = h 1 ( l ) 、 h 2 ( l ) 、 . . . , h n ( l ) H^{(l)}={h^{(l)}_1、h^{(l)}_2、...,h^{(l)}_n} H(l)=h1(l)?、h2(l)?、...,hn(l)?,我们计算从 j j j到 i i i的每条边的multi-head attention如下:
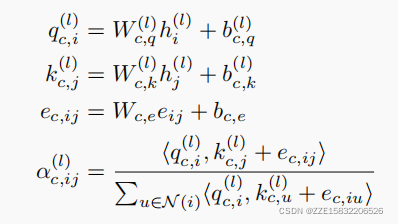
对于第C个head attention,,我们首先使用不同的可训练参数,将源特征
h
i
(
l
)
h^{(l)}_i
hi(l)?、终点特征
h
j
(
l
)
h^{(l)}_j
hj(l)?转换为query vector
q
c
,
i
(
l
)
q^{(l)}_ {c,i}
qc,i(l)?,key vector
k
c
,
j
(
l
)
k^{(l)}_{c,j}
kc,j(l)?,分别使用不同的可训练参数
W
c
,
q
(
l
)
W^{(l)}_{c,q}
Wc,q(l)?、
W
c
,
k
(
l
)
W^{(l)}_{c,k}
Wc,k(l)?、
b
c
,
q
(
l
)
b^{(l)}_{c,q}
bc,q(l)?、
b
c
,
k
(
l
)
b^{(l)}_{c,k}
bc,k(l)?。
所提供的边缘特征
e
i
j
e_{ij}
eij?将被编码并添加到关键向量中,作为每个层的附加信息
在得到了图的多头关注后,我们进行了从终点j到源点i的一个消息聚合。

其中,
∣
∣
||
∣∣是C头注意的连接操作,
此外,我们使用层间的门控残差连接以防止我们的模型过度平滑。

我们通过简单地将节点特征和标签向量相加,作为传播信息
H
0
=
X
+
Y
d
H_0=X+Y_d
H0?=X+Yd?,将标签传播结合到图变换器中。我们的模型在一个共享的消息传递框架中统一了标签传播和特征传播。

下面是整个图形的流程:
1.V,K,Q是一个三维矩阵
(
1
?
10
?
512
)
(1*10*512)
(1?10?512)
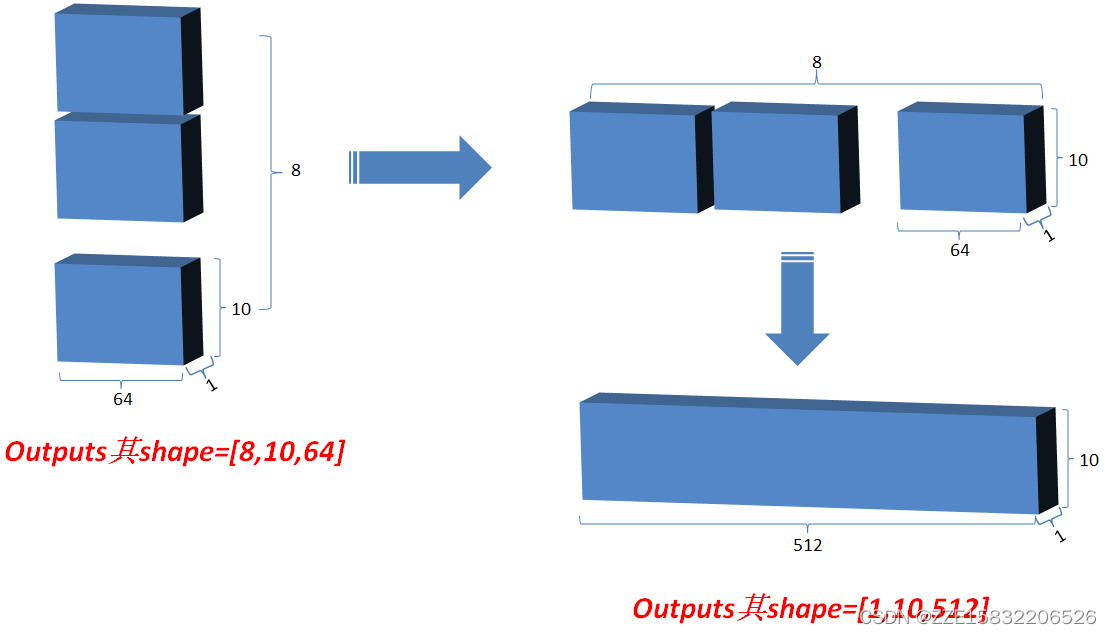
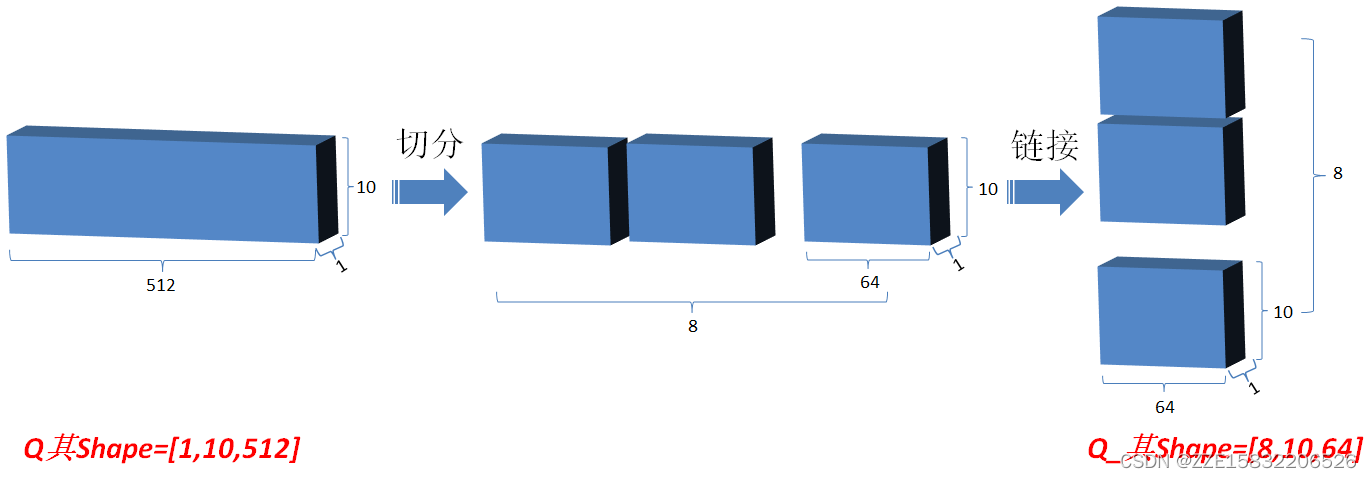
2.然后将Q在最后一维上进行切分为num_heads(假设为8)段,然后对切分完的矩阵在axis=0维上进行concat链接起来;对V和K都进行和Q一样的操作;操作后的矩阵记为Q_,K_,V_;
(
8
?
10
?
64
)
(8*10*64)
(8?10?64)
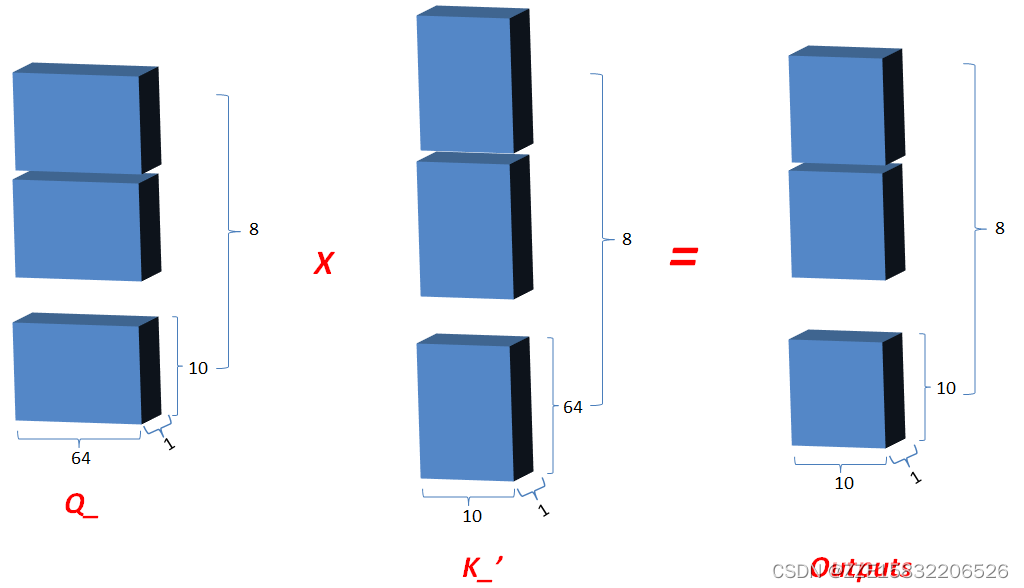
3. Q_矩阵相乘 K_的转置(对最后2维),生成结果记为outputs,然后对outputs 进行scale一次更新为outputs。
(
8
?
10
?
64
)
?
(
8
?
64
?
10
)
=
(
8
?
10
?
10
)
(8*10*64)*(8*64*10)=(8*10*10)
(8?10?64)?(8?64?10)=(8?10?10)
4.对outputs进行softmax运算,更新outputs,即outputs=softmax(outputs);
5.最新的outputs(即K和Q的相关性) 矩阵相乘 V_, 其值更新为outputs;
(
8
?
10
?
10
)
?
(
8
?
10
?
64
)
=
(
8
?
10
?
64
)
(8*10*10)*(8*10*64)=(8*10*64)
(8?10?10)?(8?10?64)=(8?10?64)
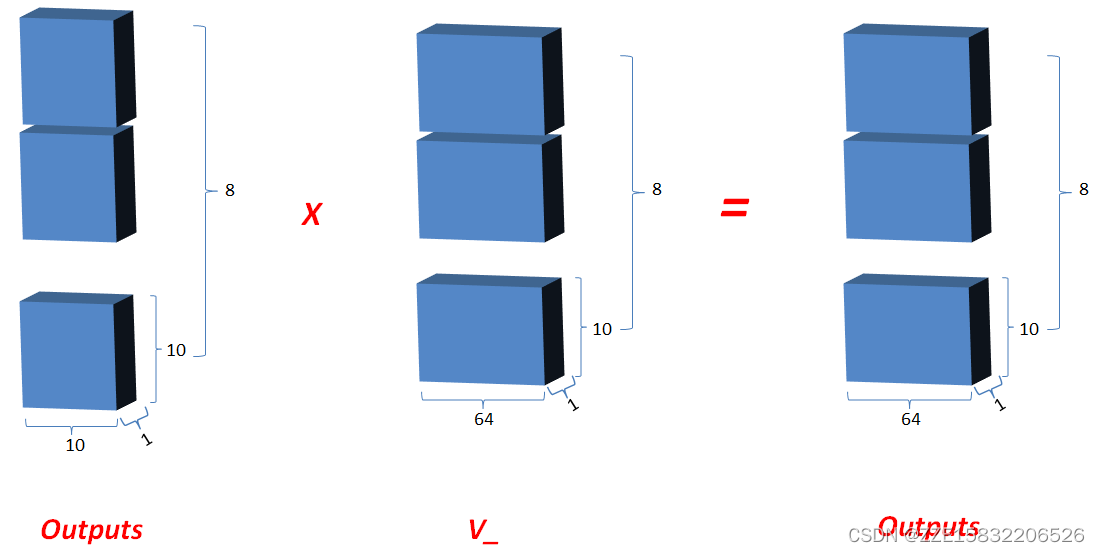
6.最后将outputs在axis=0维上切分为num_heads段,然后在axis=2维上合并, 恢复原来Q的维度;
(
1
?
10
?
512
)
(1*10*512)
(1?10?512)