[人工智能]On the Integration of Self-Attention and Convolution

论文链接：https://arxiv.org/pdf/2111.14556.pdf
本文首先证明了k×k的传统卷积可以分解为$k^2$个单独的1×1卷积。然后，将selfattention模块中queries, keys, and values的投影解释为多个1×1卷积，然后计算注意权重和values的聚合。因此，两个模块的第一阶段包括类似的操作。更重要的是，与第二阶段相比，第一阶段的计算复杂度占主导地位（通道大小的平方）。这一观察结果可以促使这两种看似截然不同的范式的完美结合，即一种既享受自我注意力又享受卷积（ACmix）好处的混合模型，同时与纯卷积或自我注意力对应模型相比，具有最小的计算开销。

一、文章改进

考虑到卷积和自注意力的不同和互补性质，通过整合这些模块，有可能从这两种范式中获益。早期阶段的研究，例如SENet，CBAM，表明自注意力机制可以作为卷积模块的增强。最近，自注意力模块被提议作为单独的模块来替代CNN模型中的传统卷积，例如SAN，BoTNet。另一个研究方向侧重于将自注意力和卷积结合在单个块中，例如AA-ResNet，Container，而该体系结构在为每个模块设计独立路径方面受到限制。因此，现有的方法仍然将自注意力和卷积视为不同的部分，它们之间的潜在关系尚未得到充分利用。
在这篇论文中，作者试图发掘自注意力和卷积之间更密切的关系。通过分解这两个模块的运算，发现它们严重依赖于相同的1×1卷积运算。基于这一观察，作者开发了一个名为ACmix的混合模型，并以最小的计算开销将自注意力和卷积巧妙地结合起来。具体来说，首先用1×1卷积投影输入特征映射，并获得丰富的中间特征。然后，按照不同的范式，即分别以自注意力和卷积的方式，重用和聚合中间特征。通过这种方式，ACmix可以享受这两个模块的好处，并有效地避免两次执行昂贵的投影操作。
本文的贡献有两个方面：
（1）揭示了自注意力和卷积之间的强大潜在关系，为理解两个模块之间的联系提供了新的视角，并为设计新的学习范式提供了启示。
（2） 自我注意和卷积模块的完美结合体现了这两个方面的优点。经验证据表明，混合模型始终优于纯卷积或自注意力模型。

（一）、Attention enhanced Convolution

多个先前提出的图像注意机制表明，它可以克服卷积网络的局部性限制。因此，许多研究人员探索了使用注意力模块或利用更多相关信息来增强卷积网络功能的可能性。特别是，SE和Gather-Excite (GE) 为每个通道重新赋予一个权重。BAM和CBAM分别对通道和空间位置重新加权，以更好地细化特征图。AA Resnet通过连接来自另一个独立的自注意力网络的注意力图来增强某些卷积层。BoTNet在模型的后期阶段用自注意力模块替代卷积。这些工作的目的是通过聚集更大范围像素的信息来设计更灵活的特征提取器。

（二）、Attention enhanced Convolution

随着Vision Transformer 的出现，许多基于Transformer的变体被提出，并在计算机视觉任务上取得了显著的改进。其中有一些研究侧重于用卷积运算补充Transformer模型，以引入额外的归纳偏置。CvT在 tokenization化过程中采用卷积，并利用步幅卷积来降低自注意力的计算复杂度。具有卷积主干的ViT建议在早期阶段增加卷积，以实现更稳定的训练。CSwinTransformer采用基于卷积的位置编码技术，并显示下游任务的改进。Conformer将Transformer与一个独立的CNN模型相结合，以整合这两个功能。

二、文章细节

（一）、Convolution

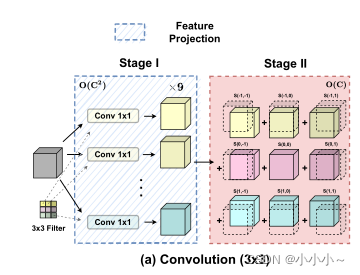
卷积是现代网络中最基本的部分之一。首先回顾标准卷积运算，并从不同的角度对其进行了重新表述。下图所示。为简单起见，我们假设卷积的步长为1。

一个标准卷积K，$K\in R^{C_{out}\times C_{in}\times k\times k}$，其中k是内核大小，$C_{in}，C_{out}$是输入和输出通道大小。给定张量$F\in R^{C_{in}\times H\times W}$，$G\in R^{C_{out}\times H\times W}$作为输入和输出特征映射，其中H，W表示高度和宽度，$f_{ij}\in R^{C_{in}}$, $g_{ij}\in R^{C_{out}}$是分别对应于F和G的像素$（i，j）$的特征张量。标准卷积可以表示为：

其中$K_{p,q}\in R^{C_{out}\times C_{in}}$， p , q ∈ { 0 , 1 ， … ， k ? 1 } p,q∈ \{0,1，…，k?1\} p,q∈{0,1，…，k?1}，表示与核位置$(p，q)$相关的核权重。
可以将等式（1）重写为内核不同位置的特征映射的总和：


为了进一步简化公式，定义移位运算$\tilde{f}?Shift(f,?x,?y)$：

$?x、?y$对应于水平和垂直位移。然后，等式（3）可以改写为：

标准卷积可以总结为两个阶段：

在第一阶段，输入特征映射是线性投影。核权重来自位置，即（p，q）。这与标准的1×1卷积相同。而在第二阶段，投影的特征映射会根据内核位置进行移动，并最终聚合在一起。可以很容易地观察到，大多数计算成本是在1×1卷积中执行的，而下面的移位和聚合是轻量级的。

(二)、Self-Attention

注意机制在视觉任务中也被广泛采用。与传统的卷积相比，注意力允许模型在更大范围内关注重要区域。如下。

一个具有n个头部的标准自注意力模块。$F\in R^{C_{in}\times H\times W}$，$G\in R^{C_{out}\times H\times W}$表示输入和输出特性。$f_{ij}\in R^{C_{in}}，g_{ij}\in R^{C_{out}}$表示像素$(i,j)$的相应张量。然后，注意力模块的输出计算为：

$||$是N个注意头输出的串联，$W_l^{(q)}、W_l^{(k)}、W_l^{(v)}$是queries, keys ,values的投影矩阵。$N_k(i，j)$表示像素的局部区域，其空间范围k以(i，j)为中心，并且$A（W_l^{(q)}{f}_{ij}、W_l^{(k)}{f}_{ab}）$是关于$N_k(i，j)$内的特征的相应注意权重。
广泛采用的自我注意模块，注意权重计算如下：

其中d是$W_q^{(l)}{f}_{ij}$的特征尺寸。
此外，多头自我注意可以分解为两个阶段，并重新表述为：

类似于传统卷积。第一阶段首先进行1×1卷积，将输入特征投影为查询、键和值。第二阶段包括注意力权重的计算和价值矩阵的聚合，即收集局部特征。与第一阶段相比，相应的计算成本也被证明是较小的，遵循与卷积相同的模式。

(三)、Computational Cost

为了充分了解卷积和自注意力模块的计算瓶颈，本文分析了每个阶段的浮点运算（FLOPs）和参数数量，并在下表中进行了总结。
1.研究表明，卷积第一阶段的理论FLOPs 和参数对于通道大小C具有二次复杂性，而第二阶段的计算成本与C呈线性关系，不需要额外的训练参数。
在自注意力模块中也有同样的情况，其中所有的训练参数被保存在阶段I。至于理论得到FLOPs，考虑正常情况下，在ReNET模型中，其中$K_a＝7$，对于不同的层深度有C＝64, 128, 256，512。结果表明，当$3C^2>2k_a^{2}C$时，第一阶段消耗的操作更重，并且随着通道大小的增加，差异更明显。

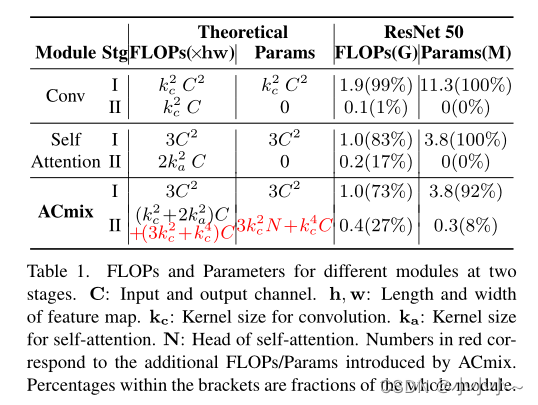
(四)、Relating Self-Attention with Convolution

自注意力和卷积模块这两个阶段的作用非常相似。第一阶段是特征学习模块，两种方法通过执行1×1卷积来共享相同的操作，从而将特征投影到更深的空间。另一方面，第二阶段对应于特征聚合的过程，尽管他们的学习范式不同。
从计算角度来看，在卷积模块和自注意力模块的第一阶段进行的1×1卷积需要理论的FLOPs和的参数与通道大小C有关的。相比之下，在第二阶段，两个模块都是轻量级的或几乎没有计算。
综上所述，上述分析表明：
（1）卷积和自注意力在通过1×1卷积投影输入特征图时实际上共享相同的操作，这也是两个模块的计算开销。
（2） 虽然对于捕获语义特征至关重要，但第二阶段的聚合操作是轻量级的，并且不会获得额外的学习参数。

（五）、Integration of Self-Attention and Convolution

上述观察结果自然会形成卷积和自注意力的完美结合。由于两个模块共享相同的1×1卷积运算，只能执行一次投影，并将这些中间特征映射分别用于不同的聚合操作。本文提出的混合模块ACmix的示意图如下所示。

ACmix包括两个阶段。在第一阶段，输入特征通过三个1×1卷积投影，并分别reshape为N个片段。因此，获得了一组包含3×N特征映射的丰富中间特征。
在第二阶段，它们按照不同的范式被使用。对于自注意力路径，将中间特征集合为N组，每组包含三个特征，每个1×1卷积一个。相应的三个特征图作为查询、键和值，遵循传统的多头自我注意模块。对于核大小为k的卷积路径，采用全连接层并生成$k^2$特征映射。因此，通过移动和聚合生成的特征，以卷积的方式处理输入特征，并像传统的那样从局部感受野收集信息。
最后，两条路径的输出相加，强度由两个可学习的标量控制：

(四)、Improved Shift and Summation

卷积路径中的中间特征遵循传统卷积模块中执行的移位和求和操作。尽管张量理论上很轻，但向不同方向移动张量实际上会破坏数据的局部性，很难实现矢量化实现。这可能会极大地损害模块在推理时的实际效率。
作为补救措施，采用固定核的深度卷积来代替低效的张量移位，如下所示。取值为（f，?1.?1） 移位特征的计算公式为：

其中c代表输入特性的每个通道。

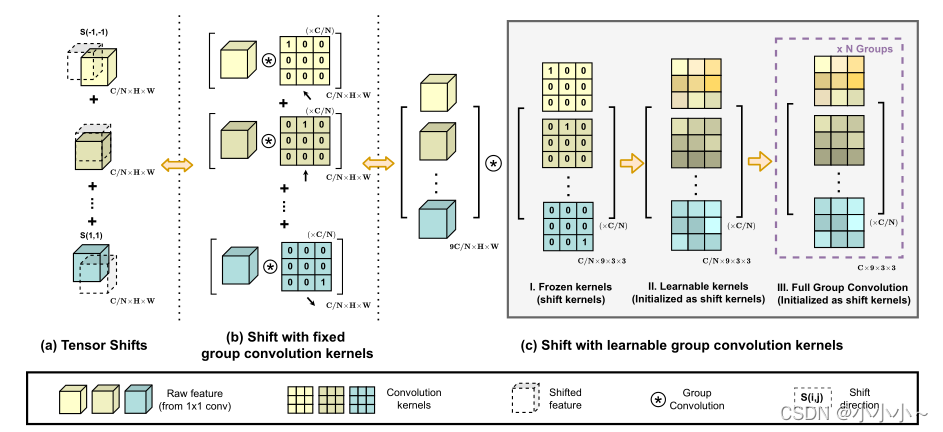
另一方面，如果我们将卷积核（核大小k=3）表示为：

相应的输出可以表示为：

因此，通过针对特定移位方向精心设计的核权重，卷积输出相当于简单的张量移位。为了进一步结合来自不同方向的特征之和，将所有输入特征和卷积核分别连接起来，并将移位运算表示为单组卷积，如上图所示。这种修改使模块具有更高的计算效率。
在此基础上，作者还引入了一些调整，以增强模块的灵活性。如上图（c.II）所示，将卷积核作为可学习的权重释放，并将移位核作为初始化。这提高了模型容量，同时保持了原始轮流操作的能力。作者还使用多组卷积核来匹配卷积和自注意力路径的输出通道维度，如上图（c.III）所示。

（五）、Generalization to Other Attention Modes

随着自注意力机制的发展，许多研究都集中在探索注意力算子的变化，以进一步提高模型的性能。。Swin Transformer采用的窗口注意力在同一个局部窗口中保持tokens的相同接受域，以节省计算成本并实现快速推理。VIT和DEIT，考虑在单个层内保持长距离依赖的全局注意力。这些修改在特定的模型架构下被证明是有效的。
在这种情况下，值得注意的是，本文提出的ACmix独立于自我注意力方法，并且可以很容易地用于上述变体。具体而言，注意力权重可以总结为：

$[?]$表示特征串联，$?(?)$表示两个具有中间非线性激活函数的线性投影层，$W_k(i，j)$表示每个查询标记的专用接收域，W表示整个特征图。然后，计算出的注意力权重可应用于等式（12），并符合一般公式。

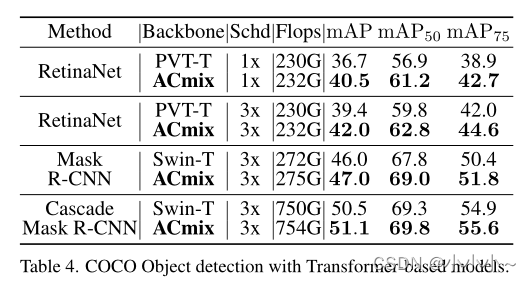
三、实验验证