视觉机器学习20讲-MATLAB源码示例(11)-流形学习算法
1. 流形学习算法
流形学习是一类借鉴了拓扑流形概念的降维方法,与核PCA的目的一样,它想要在低维空间中尽量保持在高维空间中的结构。一个形象的流形降维过程如下图,我们有一块卷起来的布,我们希望将其展开到一个二维平面,我们希望展开后的布能够在局部保持布结构的特征,其实也就是将其展开的过程,就像两个人将其拉开一样。
流形学习方法有很多种,但是他们具有一些共同的特征:首先构造流形上样本点的局部邻域结构,然后用这些局部邻域结构来将样本点全局的映射到一个低维空间。它们之间的不同之处主要是在于构造的局部邻域结构不同,以及利用这些局部邻域结构来构造全局的低维嵌入方法的不同。
2. Matlab仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:演示流形学习算法在计算机视觉中的应用
%基于流形学习实现目标分类;
%环境:Win7,Matlab2018a
%Modi: C.S
%时间:2022-04-05
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
% SWISS ROLL DATASET
N=2000;
K=12;
d=2;
clf; colordef none; colormap jet; set(gcf,'Position',[200,400,620,200]);
% PLOT TRUE MANIFOLD
tt0 = (3*pi/2)*(1+2*[0:0.02:1]); hh = [0:0.125:1]*30;
xx = (tt0.*cos(tt0))'*ones(size(hh));
yy = ones(size(tt0))'*hh;
zz = (tt0.*sin(tt0))'*ones(size(hh));
cc = tt0'*ones(size(hh));
subplot(1,3,1); cla;
surf(xx,yy,zz,cc);
view([12 20]); grid off; axis off; hold on;
lnx=-5*[3,3,3;3,-4,3]; lny=[0,0,0;32,0,0]; lnz=-5*[3,3,3;3,3,-3];
lnh=line(lnx,lny,lnz);
set(lnh,'Color',[1,1,1],'LineWidth',2,'LineStyle','-','Clipping','off');
axis([-15,20,0,32,-15,15]);
% GENERATE SAMPLED DATA
tt = (3*pi/2)*(1+2*rand(1,N)); height = 21*rand(1,N);
X = [tt.*cos(tt); height; tt.*sin(tt)];
% SCATTERPLOT OF SAMPLED DATA
subplot(1,3,2); cla;
scatter3(X(1,:),X(2,:),X(3,:),12,tt,'+');
view([12 20]); grid off; axis off; hold on;
lnh=line(lnx,lny,lnz);
set(lnh,'Color',[1,1,1],'LineWidth',2,'LineStyle','-','Clipping','off');
axis([-15,20,0,32,-15,15]); drawnow;
% RUN LLE ALGORITHM
Y=lle(X,K,d);
% SCATTERPLOT OF EMBEDDING
subplot(1,3,3); cla;
scatter(Y(1,:),Y(2,:),12,tt,'+');
grid off;
set(gca,'XTick',[]); set(gca,'YTick',[]);
3. 仿真结果
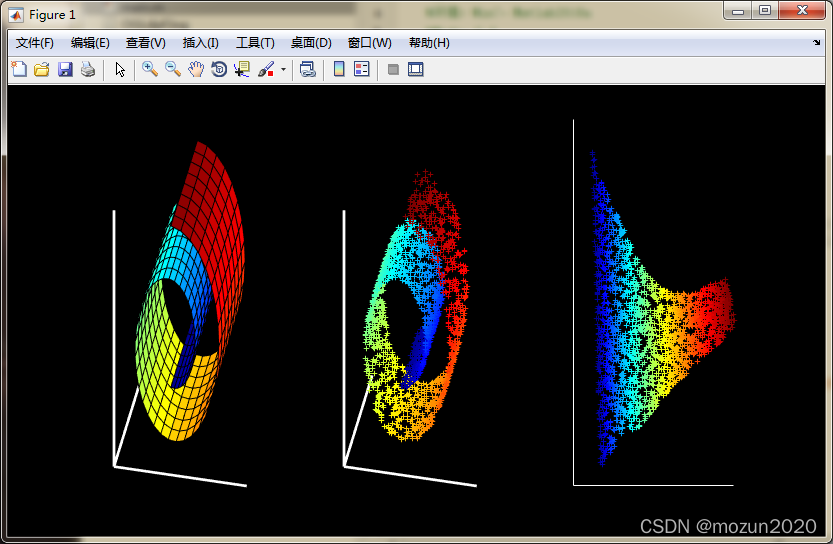
4. 小结
两种最常见的流形学习方法:Isomap和局部线性嵌入(LLE)。
局部线性嵌入(LLE)是广泛使用的图形图像降维方法,它实现简单,但是对数据的流形分布特征有严格的要求。比如不能是闭合流形,不能是稀疏的数据集,不能是分布不均匀的数据集等等,这限制了它的应用。
优点:
(1)可以学习任意维的局部线性的低维流形。
(2)算法归结为稀疏矩阵特征分解,计算复杂度相对较小,实现容易。
缺点:
(1)算法所学习的流行只能是不闭合的,且样本集是稠密均匀的。
(2)算法对最近邻样本数的选择敏感,不同的最近邻数对最后的降维结果有很大影响。
有兴趣的推荐去仔细查看全文《机器学习20讲》中第十一讲内容,以及网上关于流形学习讲解比较好的课程,深入学习了解,MATLAB仿真源码在分享的资源中已打包好,欢迎取用。