[人工智能]opencv （五十七）相机模型与投影

小白学视觉，笔记，扩展

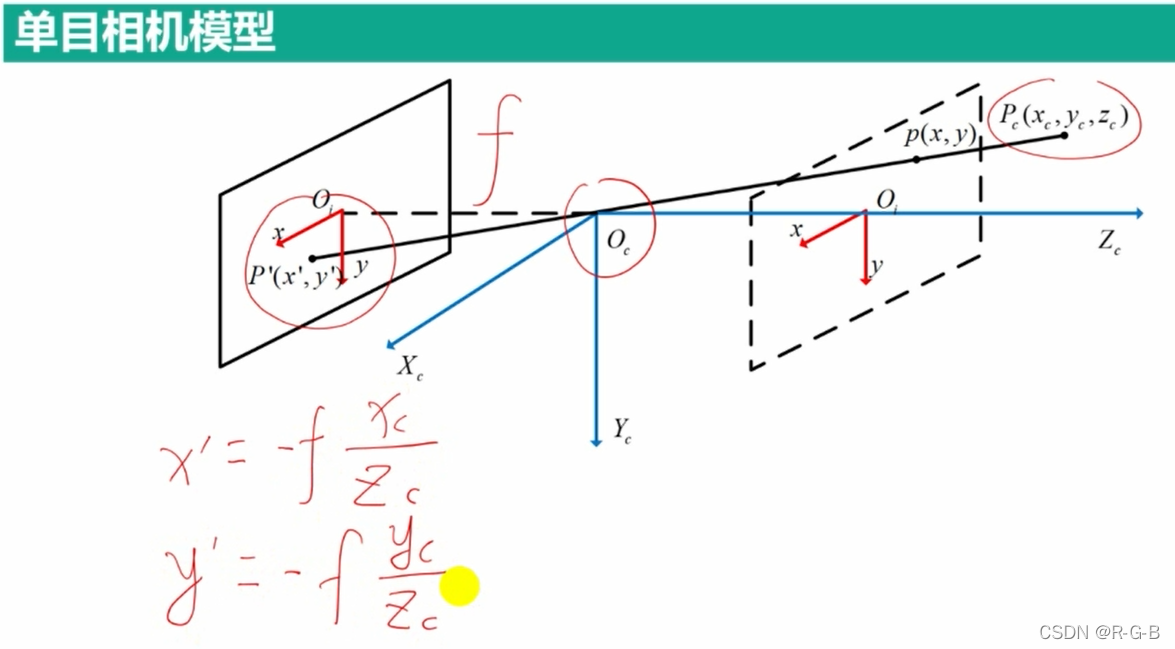
由于，x’,y’是负数，为了便于计算，将相机成像平面转放到物体同侧（光心与物体之间）
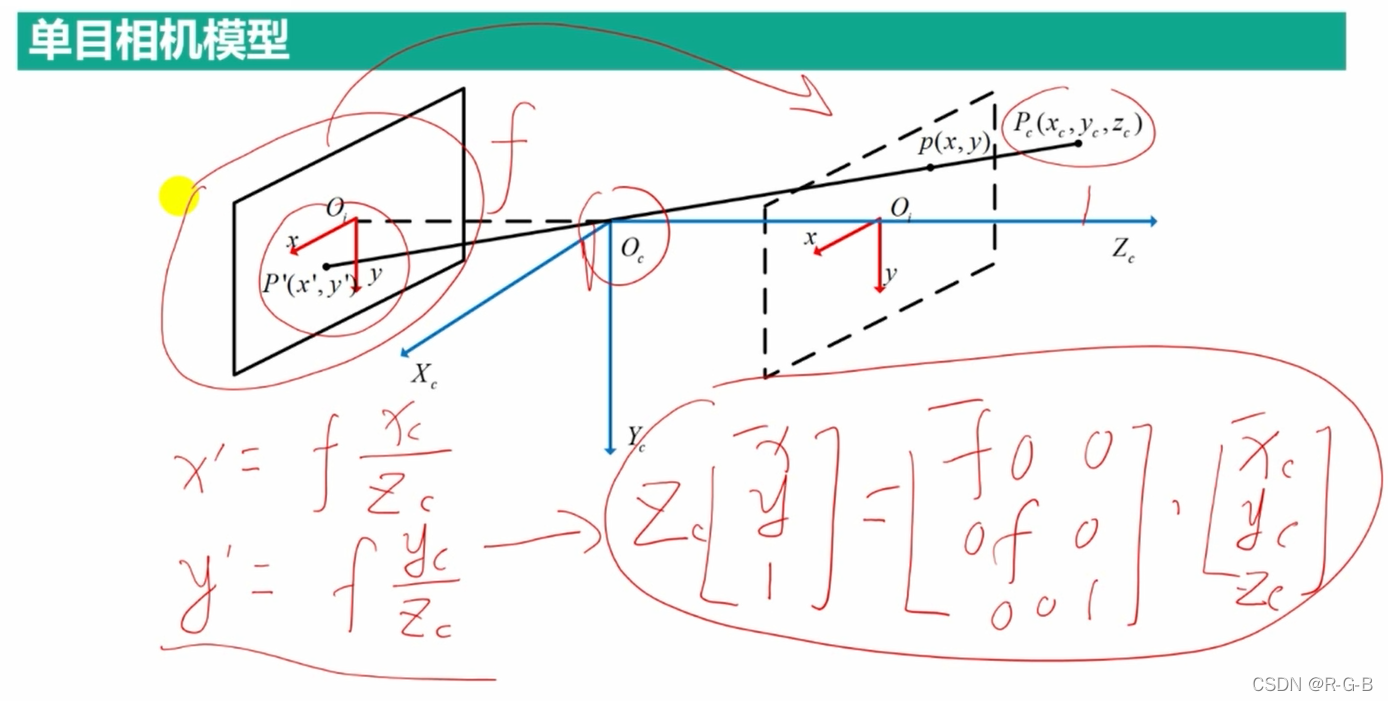
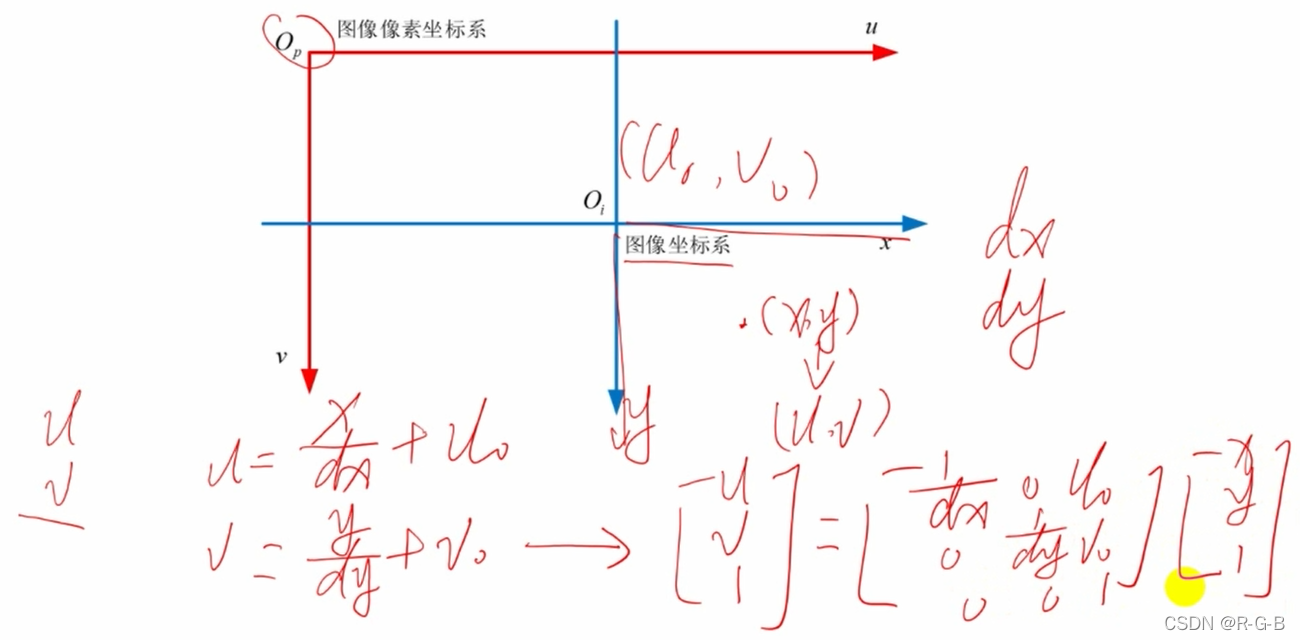
转换为齐次坐标


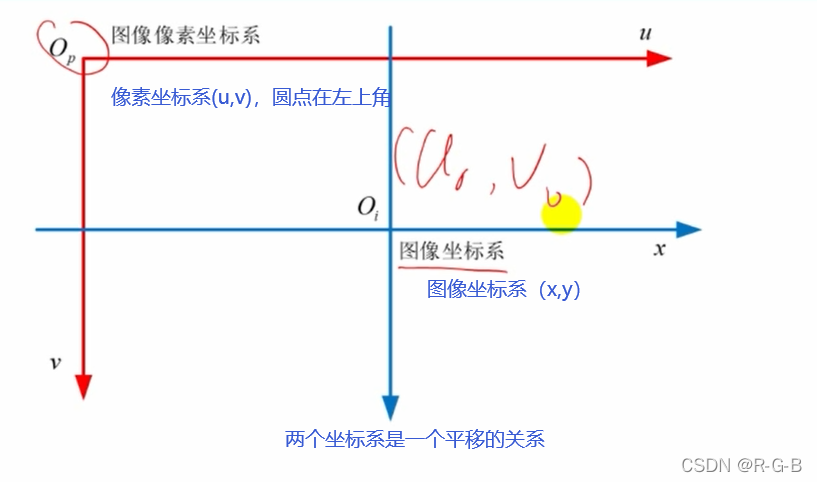
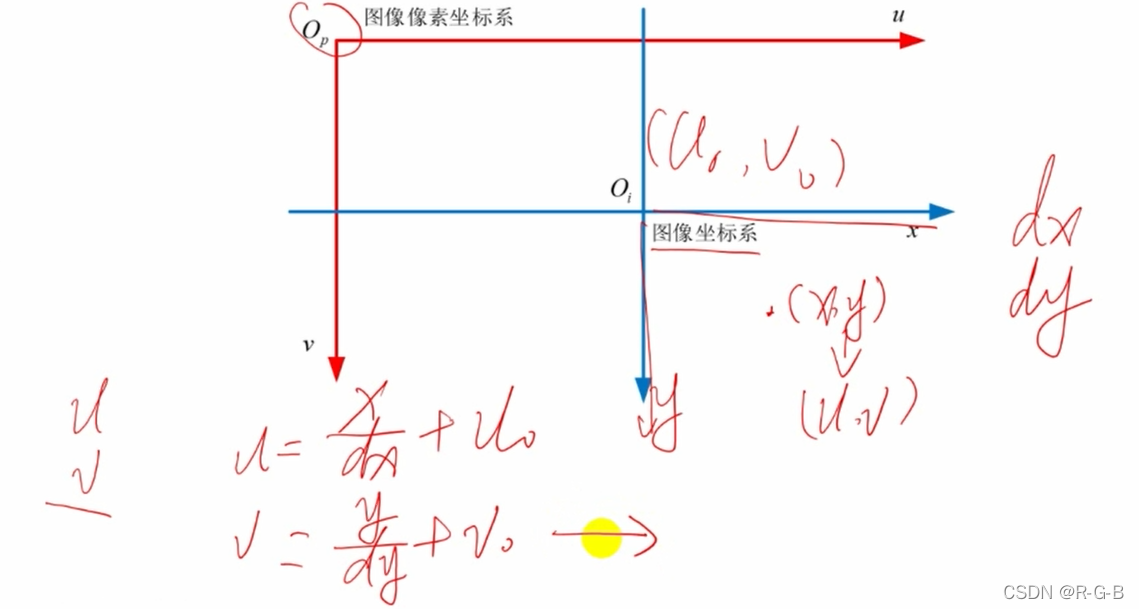
两个坐标系是一个平移的关系
假设一个像素长度和高度对应实际长度的关系为dx,dy

将空间坐标（x,y）坐标转换为像素坐标

转换为齐次坐标

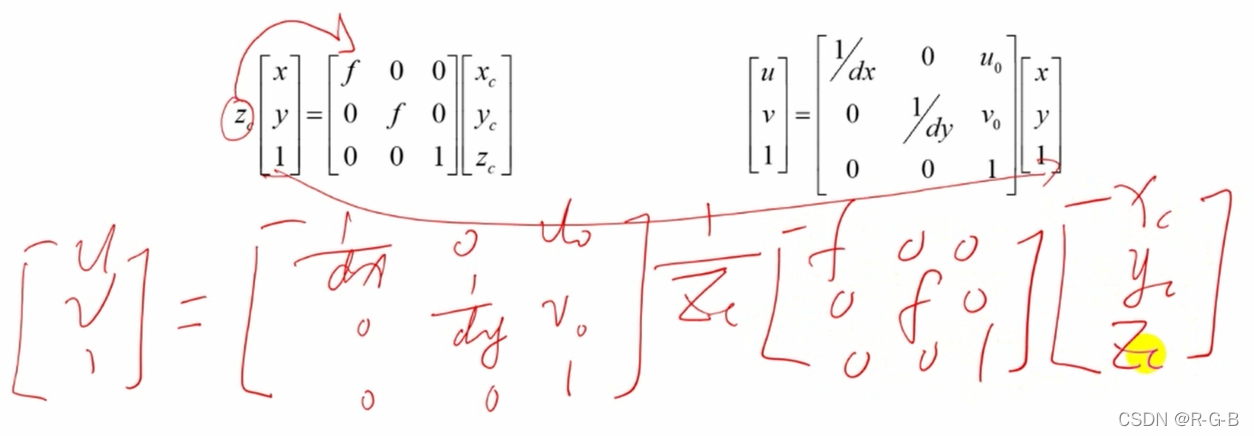
三维空间映射到二维平面

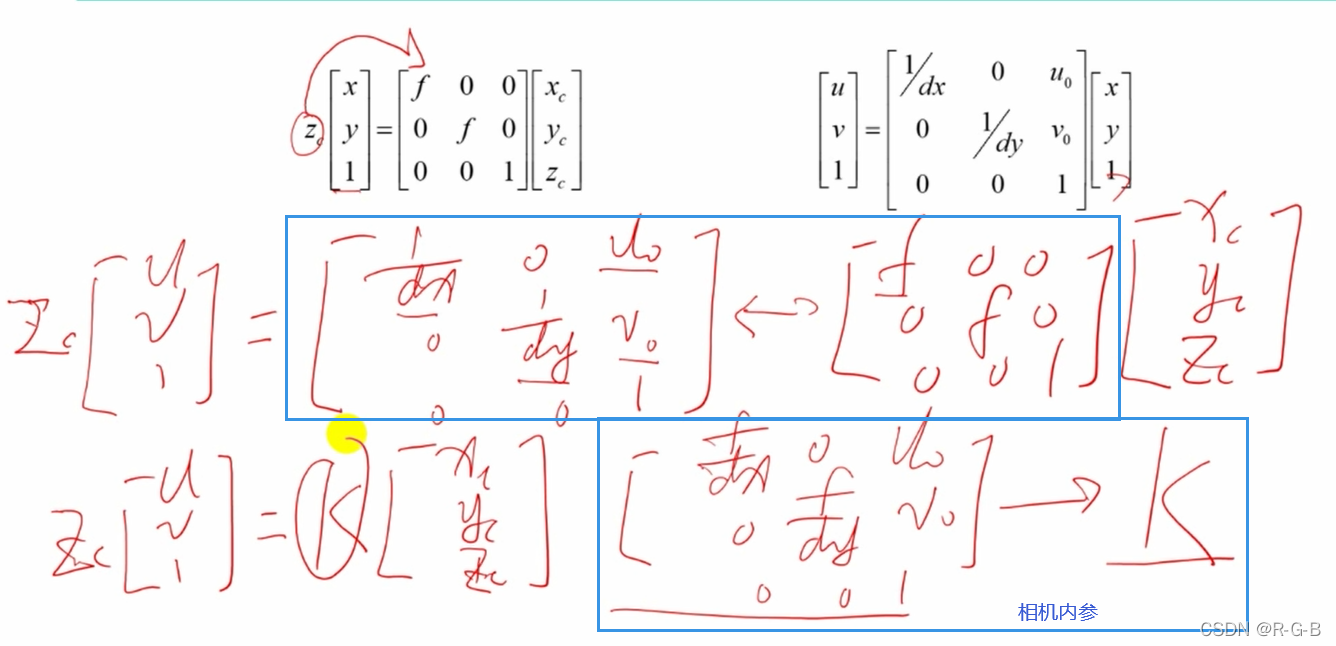
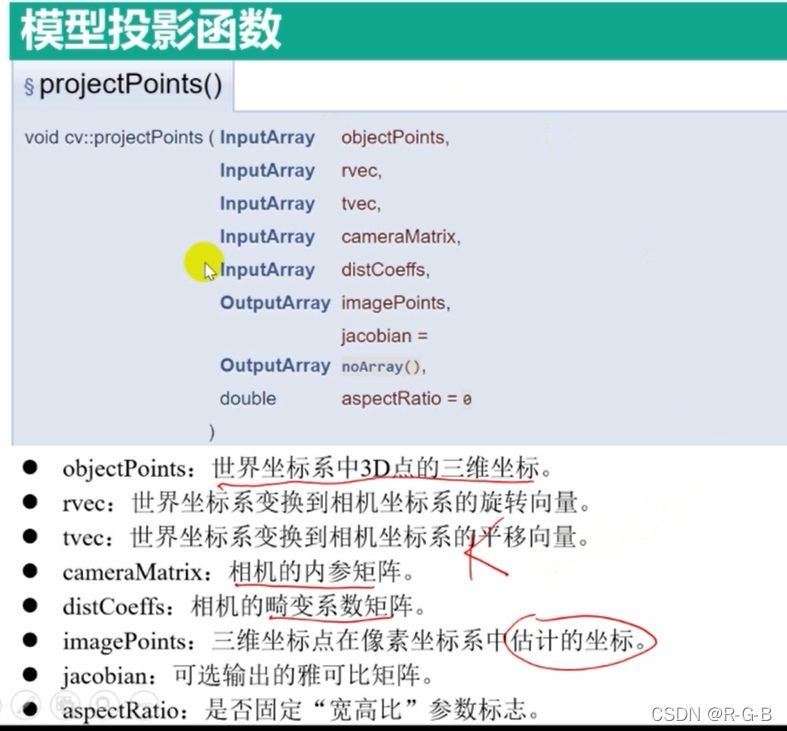
include <opencv2\opencv.hpp>
#include <iostream>
#include <vector>

using namespace std;
using namespace cv;

int main()
{

	//输入计算得到的内参矩阵和畸变矩阵（相机商家会提供，但最好还是标定一遍）
	Mat cameraMatrix = (Mat_<float>(3, 3) << 532.016297, 0, 332.172519,
		0, 531.565159, 233.388075,
		0, 0, 1);
	Mat distCoeffs = (Mat_<float>(1, 5) << -0.285188, 0.080097, 0.001274,
		-0.002415, 0.106579);
	//前面已经计算好的
	//代码清单10-10中计算的第一张图像相机坐标系与世界坐标系之间的关系
	Mat rvec = (Mat_<float>(1, 3) << -1.977853, -2.002220, 0.130029);
	Mat tvec = (Mat_<float>(1, 3) << -26.88155, -42.79936, 159.19703);

	//生成第一张图像中内角点的三维世界坐标
	Size boardSize = Size(9, 6);//标定板的内角点数目
	Size squareSize = Size(10, 10);  //棋盘格每个方格的真实尺寸
	vector<Point3f> PointSets;
	for (int j = 0; j < boardSize.height; j++)
	{
		for (int k = 0; k < boardSize.width; k++)
		{
			Point3f realPoint;
			// 假设标定板为世界坐标系的z平面，即z=0
			realPoint.x = j * squareSize.width;
			realPoint.y = k * squareSize.height;
			realPoint.z = 0;
			PointSets.push_back(realPoint);
		}
	}

	//根据三维坐标和相机与世界坐标系时间的关系估计内角点像素坐标
	vector<Point2f> imagePoints;
	projectPoints(PointSets, rvec, tvec, cameraMatrix, distCoeffs, imagePoints);

	for (int i = 0; i < imagePoints.size(); i++)
	{
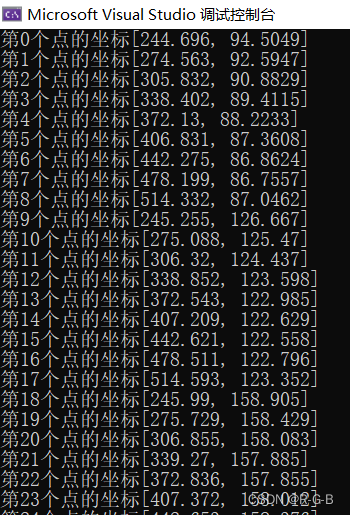
		cout << "第" << to_string(i) << "个点的坐标" << imagePoints[i] << endl;

	}
	waitKey(0);
	return 0;
}

输出6*9=54个像素点