[人工智能]乘同余法(Congruential Method)

乘同余法(Congruential Method)

乘同余法(Congruential Method)如今比较流行并且用得最多的是同余产生器。乘同余法是由Lehmer在1951年提出来的，它的一般形式是:

对于任一初始值$x_1$，伪随机数序列由下面递推公式确定:

$$x_n=a?x_{n?1}(\mathrm{m}\mathrm{o}\mathrm{d}M)$$
$${\xi }_n=\frac{x_n}{M}n=1,2,?$$ 其中：

$x_0$–种子（或初始值seed）

$a$–乘子（乘法器multiplier）

$M$–模 (模数modulus)

$\mathrm{m}\mathrm{o}\mathrm{d}$–取模运算

利用乘同余法,选$A=5^6$,$M=256$,递推100次,产生(-1,1)均匀分布随机数。采用MATLAB仿真语言编程,程序运行结果如图1所示。

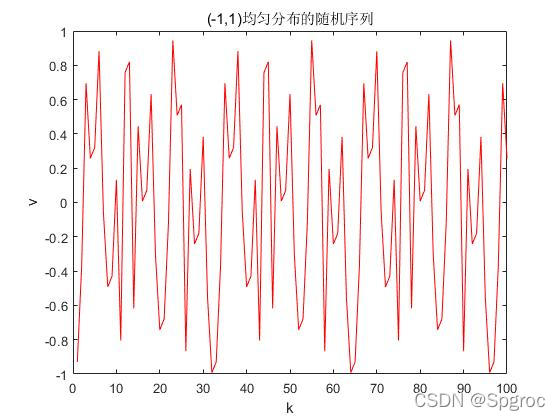
产生的(-1,1)均匀分布随机序列如下:

-0.92969   -0.36719   0.695313   0.257813   0.320313   0.882813   -0.05469   -0.49219   -0.42969   0.132813
-0.80469   0.757813   0.820313   -0.61719   0.445313   0.007813   0.070313   0.632813   -0.30469   -0.74219
-0.67969   -0.11719   0.945313   0.507813   0.570313   -0.86719   0.195313   -0.24219   -0.17969   0.382813
-0.55469   -0.99219   -0.92969   -0.36719   0.695313   0.257813   0.320313   0.882813   -0.05469   -0.49219
-0.42969   0.132813   -0.80469   0.757813   0.820313   -0.61719   0.445313   0.007813   0.070313   0.632813
-0.30469   -0.74219   -0.67969   -0.11719   0.945313   0.507813   0.570313   -0.86719   0.195313   -0.24219
-0.17969   0.382813   -0.55469   -0.99219   -0.92969   -0.36719   0.695313   0.257813   0.320313   0.882813
-0.05469   -0.49219   -0.42969   0.132813   -0.80469   0.757813   0.820313   -0.61719   0.445313   0.007813
0.070313   0.632813   -0.30469   -0.74219   -0.67969   -0.11719   0.945313   0.507813   0.570313   -0.86719
0.195313   -0.24219   -0.17969   0.382813   -0.55469   -0.99219   -0.92969   -0.36719   0.695313   0.257813

乘同余法MATLAB代码:

%% 同余法产生白噪声
clear all;
close all;
A=5^6;N=100;x0=1;k=8;M=2.^k; %参数初始化
for k=1:N %乘同余法递推100次开始
    x2=A*x0;
    x1=mod(x2,M); %将x2存储器的数除以M,取余数放入x1中
    v1=x1/M;      %将x1存储器中的数除以u得到随机数
    x0=x1;
    v0=2*(v1-0.5); %映射到（-1，1）
    v(:,k)=v0;    %将v1中的数存放在矩阵v中的第k列
end   %递推100次结束
v2=reshape(v,5,20)'; %将矩阵v中的随机数存放在v2中
% grapher 绘图
k1=k;
k=1:k1;
plot(k,v,'r');
xlabel('k'),ylabel('v');
title('(-1,1)均匀分布的随机序列')

本文是数据驱动智能建模方法的作业记录，同时记录一下LATEX模板，表格、代码的插入，主要参考 系统辨识理论及MATLAB仿真__刘金琨编

\documentclass[UTF8]{ctexart}

\title{数据驱动智能建模方法-作业}
\author{xxx}
\date{\today}
\usepackage{cases}
\usepackage{color}
\usepackage{listings} 
\usepackage{xcolor}
\usepackage{graphicx}
\usepackage{geometry}
\geometry{a4paper,scale=0.8}
\usepackage{fancyhdr}
\pagestyle{fancy}
\lfoot{}%这条语句可以让页码出现在下方

\lstset{
  language=Matlab,  %代码语言使用的是matlab
  frame=shadowbox, %把代码用带有阴影的框圈起来
  rulesepcolor=\color{red!20!green!20!blue!20},%代码块边框为淡青色
  keywordstyle=\color{blue!90}\bfseries, %代码关键字的颜色为蓝色，粗体
  commentstyle=\color{red!10!green!70}\textit,    % 设置代码注释的颜色
  showstringspaces=false,%不显示代码字符串中间的空格标记
  numbers=left, % 显示行号
  numberstyle=\tiny,    % 行号字体
  stringstyle=\ttfamily, % 代码字符串的特殊格式
  breaklines=true, %对过长的代码自动换行
  extendedchars=false,  %解决代码跨页时，章节标题，页眉等汉字不显示的问题
%   escapebegin=\begin{CJK*},escapeend=\end{CJK*},      % 代码中出现中文必须加上，否则报错
  texcl=true}
\begin{document} 
\maketitle 
\section*{乘同余法(Congruential Method)}    
乘同余法(Congruential Method)
如今比较流行并且用得最多的是同余产生器。乘同余法是由Lehmer在1951年提出来的，它的一般形式是:


对于任一初始值$x_1$，伪随机数序列由下面递推公式确定:

$$
x_{n}=a \cdot x_{n-1}(\bmod M) 
$$
$$
\xi_{n}=\frac{x_{n}}{M}\qquad n=1,2, \cdots
$$
其中：


\centerline{$x_{0}$--种子（或初始值seed）}
\centerline{${a}$--乘子（乘法器multiplier）}
\centerline{${M}$--模 (模数modulus)}
\centerline{$\bmod$--取模运算}

利用乘同余法,选$A=5^6$,$M=256$,递推100次,产生(-1,1)均匀分布随机数。采用MATLAB仿真语言编程,程序运行结果如图1所示。

\begin{figure}[htb]
	\centering
	\centerline{\includegraphics[scale=0.5]{photo.jpg}}
	\caption{均匀分布白噪声曲线}
	\label{fig}	
\end{figure}
\clearpage
产生的(-1,1)均匀分布随机序列如下:
% Table generated by Excel2LaTeX from sheet 'Sheet1'
\begin{table}[htbp]
  \centering
  \caption{均匀分布随机序列}
    \begin{tabular}{rrrrrrrrrr}
    -0.92969 & -0.36719 & 0.695313 & 0.257813 & 0.320313 & 0.882813 & -0.05469 & -0.49219 & -0.42969 & 0.132813 \\
    -0.80469 & 0.757813 & 0.820313 & -0.61719 & 0.445313 & 0.007813 & 0.070313 & 0.632813 & -0.30469 & -0.74219 \\
    -0.67969 & -0.11719 & 0.945313 & 0.507813 & 0.570313 & -0.86719 & 0.195313 & -0.24219 & -0.17969 & 0.382813 \\
    -0.55469 & -0.99219 & -0.92969 & -0.36719 & 0.695313 & 0.257813 & 0.320313 & 0.882813 & -0.05469 & -0.49219 \\
    -0.42969 & 0.132813 & -0.80469 & 0.757813 & 0.820313 & -0.61719 & 0.445313 & 0.007813 & 0.070313 & 0.632813 \\
    -0.30469 & -0.74219 & -0.67969 & -0.11719 & 0.945313 & 0.507813 & 0.570313 & -0.86719 & 0.195313 & -0.24219 \\
    -0.17969 & 0.382813 & -0.55469 & -0.99219 & -0.92969 & -0.36719 & 0.695313 & 0.257813 & 0.320313 & 0.882813 \\
    -0.05469 & -0.49219 & -0.42969 & 0.132813 & -0.80469 & 0.757813 & 0.820313 & -0.61719 & 0.445313 & 0.007813 \\
    0.070313 & 0.632813 & -0.30469 & -0.74219 & -0.67969 & -0.11719 & 0.945313 & 0.507813 & 0.570313 & -0.86719 \\
    0.195313 & -0.24219 & -0.17969 & 0.382813 & -0.55469 & -0.99219 & -0.92969 & -0.36719 & 0.695313 & 0.257813 \\
    \end{tabular}%
  \label{tab:addlabel}%
\end{table}%




乘同余法MATLAB代码:
\begin{lstlisting}
%% 同余法产生白噪声
clear all;
close all;
A=5^6;N=100;x0=1;k=8;M=2.^k; %参数初始化
for k=1:N %乘同余法递推100次开始
    x2=A*x0;
    x1=mod(x2,M); %将x2存储器的数除以M,取余数放入x1中
    v1=x1/M;      %将x1存储器中的数除以u得到随机数
    x0=x1;
    v0=2*(v1-0.5); %映射到（-1，1）
    v(:,k)=v0;    %将v1中的数存放在矩阵v中的第k列
end   %递推100次结束
v2=reshape(v,5,20)'; %将矩阵v中的随机数存放在v2中
% grapher 绘图
k1=k;
k=1:k1;
plot(k,v,'r');
xlabel('k'),ylabel('v');
title('(-1,1)均匀分布的随机序列')
\end{lstlisting}



\end{document}