论文地址:https://arxiv.org/abs/1902.07153
一、简介
? 图卷积神经网络( Graph?Convolutional?Networks,GCNs \text{Graph Convolutional Networks,GCNs} Graph?Convolutional?Networks,GCNs)是卷积神经网络在图数据上的变体,其通过在非线性函数前堆叠若干个一阶谱过滤器来学习图数据的表示。近期, GCNs \text{GCNs} GCNs及其变体在各种图应用领域都实现了state-of-the-art。但是,由于 GCNs \text{GCNs} GCNs是在神经网络“复兴”后提出的,因此不可避免的继承了神经网络的复杂性和难以解释性。
? 本文认为对于那些需求低的应用来说, GCNs \text{GCNs} GCNs继承自神经网络的复杂性是不必要的。因此,本文的目标是推断出在 GCN \text{GCN} GCN之前基于"传统"路径能够获得的最简单模型。具体来说,本文通过移除 GCNs \text{GCNs} GCNs层之间的非线性并简化结果函数为单一线性变换,从而减少了 GCNs \text{GCNs} GCNs的额外复杂性。实验显示,最终得到的模型可以与 GCNs \text{GCNs} GCNs像媲美,且计算效率更高、拟合参数更少。本文将这个模型称为 SGC(Simple?Graph?Convolution) \text{SGC(Simple Graph Convolution)} SGC(Simple?Graph?Convolution)。
? 直觉上, SGC \text{SGC} SGC是可解释的,且本文从图卷积的角度提供了理论分析。 SGC \text{SGC} SGC中的特征抽取对应于单个固定的过滤器。 Kipf&Welling \text{Kipf\&Welling} Kipf&Welling发现 renormalization?trick \text{renormalization trick} renormalization?trick能够改善任务准确率,本文证明这个方法能够有效的缩小图的谱域,且应用在 SGC \text{SGC} SGC上能够产生低通过滤器。
? 通过在基准数据集上的评估,展示了 SGC \text{SGC} SGC能够与 GCNs \text{GCNs} GCNs及其他state-of-the-art图神经网络媲美。然而, SGC \text{SGC} SGC的速度会快很多,甚至在最大的评估数据集上比 FastGCN \text{FastGCN} FastGCN快2个数量集。此外,本文还证明了 SGC \text{SGC} SGC能够有效的扩展至下游任务中。
二、方法
? GCNs \text{GCNs} GCNs将带有部分标签的节点作为输入,并为图中的所有节点生成预测标签。形式化地,定义一个图为 G = ( V , A ) \mathcal{G}=(\mathcal{V},\textbf{A}) G=(V,A),其中 V \mathcal{V} V表示由节点 { v 1 , … , v n } \{v_1,\dots,v_n\} {v1?,…,vn?}组成的顶点集合; A ∈ R n × n \textbf{A}\in\mathbb{R}^{n\times n} A∈Rn×n是对称邻接矩阵,其中 a i j a_{ij} aij?表示节点 v i v_i vi?和 v j v_j vj?的权重,缺失的边通过 a i j = 0 a_{ij}=0 aij?=0来表示。定义度矩阵 D = diag ( d 1 , … , d n ) \textbf{D}=\text{diag}(d_1,\dots,d_n) D=diag(d1?,…,dn?)为一个对角矩阵,其对角线上的每个分量是等于邻接矩阵的行求和 d i = ∑ j a i j d_i=\sum_j a_{ij} di?=∑j?aij?。
? 图中的每个节点 v i v_i vi?对应一个 d d d维特征向量 x i ∈ R d \textbf{x}_i\in\mathbb{R}^d xi?∈Rd。整个特征矩阵 X ∈ n × d \textbf{X}\in\mathbb{n\times d} X∈n×d则是堆叠了 n n n个特征向量,即 X = [ x 1 , … , x n ] ? \textbf{X}=[\textbf{x}_1,\dots,\textbf{x}_n]^\top X=[x1?,…,xn?]?。每个节点都属于 C C C个类别中的一个,并使用 C C C维one-hot编码向量 y i ∈ { 0 , 1 } C \textbf{y}_i\in\{0,1\}^C yi?∈{0,1}C表示。
? 模型仅知道一部分节点的标签,并希望预测节点的未知标签。
1. 图卷积神经网络 GCN \text{GCN} GCN
? 类似于
CNN
\text{CNN}
CNN或者
MLP
\text{MLP}
MLP,
GCN
\text{GCN}
GCN也是通过多个层来从每个节点的特征
x
i
\textbf{x}_i
xi?中学习新的特征表示,并用线性分类器进行分类。对于第
k
k
k个图卷积层来说,所有节点的输入表示为矩阵
H
(
k
?
1
)
\textbf{H}^{(k-1)}
H(k?1),输出节点表示为
H
(
k
)
\textbf{H}^{(k)}
H(k)。自然而然地,初始化节点表示就是原始输入的特征:
H
(
0
)
=
X
(1)
\textbf{H}^{(0)}=\textbf{X} \tag{1}
H(0)=X(1)
其作为第1个
GCN
\text{GCN}
GCN的输入。
? 一个 K \text{K} K层的 GCN \text{GCN} GCN等同于在图中的每个节点特征 x i \textbf{x}_i xi?上应用 K \text{K} K层的 MLP \text{MLP} MLP,且每个节点的向量表示都是平均了其邻居节点的表示。在每个图卷积层中,节点的向量表示会在三个阶段被更新:(1) 特征传播;(2) 线性变换; (3) 非线性激活函数。
1.1 特征传播
?
GCN
\text{GCN}
GCN与
MLP
\text{MLP}
MLP的主要区别就是特征传播。在每层的开始,每个节点
v
i
v_i
vi?的特征
h
i
\textbf{h}_i
hi?是平均了它局部邻居的特征向量
h
ˉ
i
(
k
)
←
1
d
i
+
1
h
i
(
k
?
1
)
+
∑
j
=
1
n
a
i
j
(
d
i
+
1
)
(
d
j
+
1
)
h
j
(
k
?
1
)
(2)
\bar{\textbf{h}}_i^{(k)}\leftarrow\frac{1}{d_i+1}\textbf{h}_i^{(k-1)}+\sum_{j=1}^n\frac{a_{ij}}{\sqrt{(d_i+1)(d_j+1)}}\textbf{h}_j^{(k-1)} \tag{2}
hˉi(k)?←di?+11?hi(k?1)?+j=1∑n?(di?+1)(dj?+1)?aij??hj(k?1)?(2)
为了更加紧凑,这里将整个图上的更新表示为简单的矩阵操作。具体来说,令
S
\textbf{S}
S表示规范化邻接矩阵
S
=
D
~
?
1
/
2
A
~
D
~
?
1
/
2
(3)
\textbf{S}=\tilde{\textbf{D}}^{-1/2}\tilde{\textbf{A}}\tilde{\textbf{D}}^{-1/2} \tag{3}
S=D~?1/2A~D~?1/2(3)
其中,
A
~
=
A+I
\tilde{\textbf{A}}=\textbf{A+I}
A~=A+I且
D
~
\tilde{\textbf{D}}
D~是
A
~
\tilde{\textbf{A}}
A~的度矩阵。那么,等式
(
2
)
(2)
(2)中所有节点的同步更新能够简化为一个稀疏矩阵乘法
H
~
(
k
)
←
SH
(
k
?
1
)
(4)
\tilde{\textbf{H}}^{(k)}\leftarrow \textbf{SH}^{(k-1)} \tag{4}
H~(k)←SH(k?1)(4)
直觉上,这步操作沿着图的边平滑了局部向量表示,并且鼓励局部的点具有相似的预测。
1.2 线性变换与非线性激活
? 经过局部平滑后,
GCN
\text{GCN}
GCN层与
MLP
\text{MLP}
MLP层等价。每个层都被关联一个可学习权重
Θ
(
k
)
\Theta^{(k)}
Θ(k),用于对经过平滑的特征向量进行线性变换。最后,在特征向量
H
(
k
)
\textbf{H}^{(k)}
H(k)输出前,使用
ReLU
\text{ReLU}
ReLU这样的非线性激活函数对输出进行变换。整体来说,第
k
k
k层的向量表示更新规则为
H
(
k
)
←
ReLU
(
H
~
(
k
)
Θ
(
k
)
)
(5)
\textbf{H}^{(k)}\leftarrow \text{ReLU}(\tilde{\textbf{H}}^{(k)}\Theta^{(k)}) \tag{5}
H(k)←ReLU(H~(k)Θ(k))(5)
1.3 分类器
? 类似于
MLP
\text{MLP}
MLP,对于节点分类任务,
GCN
\text{GCN}
GCN会在最后一层使用
softmax
\text{softmax}
softmax分类器预测标签概率。
n
n
n个节点的类别预测表示为
Y
^
∈
R
n
×
C
\hat{\textbf{Y}}\in\mathbb{R}^{n\times C}
Y^∈Rn×C,其中
y
^
i
c
\hat{y}_{ic}
y^?ic?表示节点
i
i
i属于类别
c
c
c的概率。
GCN
\text{GCN}
GCN第
K
K
K层的类别预测记为
Y
^
GCN
=
softmax
(
SH
(
K
?
1
)
Θ
(
K
)
)
(6)
\hat{\textbf{Y}}_{\text{GCN}}=\text{softmax}(\textbf{SH}^{(K-1)}\Theta^{(K)}) \tag{6}
Y^GCN?=softmax(SH(K?1)Θ(K))(6)
其中,
softmax
(
x
)
=
exp
(
x
)
/
∑
c
=
1
C
exp
(
x
c
)
\text{softmax}(\textbf{x})=\text{exp}(\textbf{x})/\sum_{c=1}^C\text{exp}(x_c)
softmax(x)=exp(x)/∑c=1C?exp(xc?)。
2. SGC(Simple?Graph?Convolution) \text{SGC(Simple Graph Convolution)} SGC(Simple?Graph?Convolution)
? 在传统的 MLP \text{MLP} MLP层中,更深的层能够增加表达能力。因此,深层的 MLP \text{MLP} MLP能够构建特征的层次结构,即第二层的特征是在第一层特征的基础上构建的。在 GCNs \text{GCNs} GCNs中,这些层还有第二个重要作用:每层的隐藏表示会被其一跳邻居平均。这也意味着,一个经过 k k k层的阶段特征来源于其在图中的所有 k k k跳邻居。这种方式类似于卷积神经网络,模型深度增加的同时也增加了特征的感知域。虽然随着深度的增加,卷积网络的效果会变好,但是典型的 MLP \text{MLP} MLP在3或4层之后就收益很小了。
2.1 线性化
? 假设两个
GCN
\text{GCN}
GCN层间的非线性变换并不是必须的,模型的收益主要来自于局部平均。那么,移除每层的非线性变换并保留最后的
softmax
\text{softmax}
softmax。这样得到的模型仍然是线性的,且与
K
K
K层的
GCN
\text{GCN}
GCN具有相同的感知域
Y
^
=
softmax
(
S
…
SSX
Θ
(
1
)
Θ
(
2
)
…
Θ
(
k
)
)
(7)
\hat{\textbf{Y}}=\text{softmax}(\textbf{S}\dots\textbf{SSX}\Theta^{(1)}\Theta^{(2)}\dots\Theta^{(k)}) \tag{7}
Y^=softmax(S…SSXΘ(1)Θ(2)…Θ(k))(7)
为了简化表示,将规范化邻接矩阵的重复乘法表示为
S
\textbf{S}
S的
K
K
K次方法
S
K
\textbf{S}^K
SK。此外,将权重矩阵重新参数化为单一的矩阵
Θ
=
Θ
(
1
)
Θ
(
2
)
…
Θ
(
K
)
\Theta=\Theta^{(1)}\Theta^{(2)}\dots\Theta^{(K)}
Θ=Θ(1)Θ(2)…Θ(K)。那么最终的分类器表示为
Y
^
SGC
=
softmax
(
S
K
X
Θ
)
(8)
\hat{\textbf{Y}}_{\text{SGC}}=\text{softmax}(\textbf{S}^K\textbf{X}\Theta) \tag{8}
Y^SGC?=softmax(SKXΘ)(8)
本文将其称为
SGC(Simple?Graph?Convolution)
\text{SGC(Simple Graph Convolution)}
SGC(Simple?Graph?Convolution)。
2.2 Logistic回归
? 通过观察等式 ( 8 ) (8) (8)能够获得 SGC \text{SGC} SGC的直觉解释:分离特征抽取和分类器。即 SGC \text{SGC} SGC可以看做是由一个固定的特征抽取/平滑组件 X ˉ = S K X \bar{\textbf{X}}=\textbf{S}^K\textbf{X} Xˉ=SKX,后面跟一个线性 logistic \text{logistic} logistic回归分类器 Y ^ = softmax ( X ˉ Θ ) \hat{\textbf{Y}}=\text{softmax}(\bar{\textbf{X}}\Theta) Y^=softmax(XˉΘ)组成。由于 X ˉ \bar{\textbf{X}} Xˉ不需要权重,因此计算 X ˉ \bar{\textbf{X}} Xˉ就等价于特征预处理步骤。整个模型的训练就变成了在预处理特征 X ˉ \bar{\textbf{X}} Xˉ上的直接进行多类别 logistic \text{logistic} logistic回归。
三、谱分析( Spectral?Analysis \text{Spectral Analysis} Spectral?Analysis)
1. 图卷积
? 图数据上的 Fourier \text{Fourier} Fourier分析依赖于图 Laplacian \text{Laplacian} Laplacian算子的谱分解。
? 图
Laplacian
\text{Laplacian}
Laplacian矩阵
Δ
=
D-A
\Delta=\textbf{D-A}
Δ=D-A(规范化版本
Δ
s
y
m
=
D
?
1
/
2
Δ
D
?
1
/
2
\Delta_{sym}=\textbf{D}^{-1/2}\Delta\textbf{D}^{-1/2}
Δsym?=D?1/2ΔD?1/2)为对称正定矩阵。该矩阵的特征分解为
Δ
=
U
Λ
U
?
\Delta=\textbf{U}\Lambda\textbf{U}^\top
Δ=UΛU?,其中
U
∈
R
n
×
n
\textbf{U}\in\mathbb{R}^{n\times n}
U∈Rn×n是由正交特征向量组成,且
Λ
=
diag
(
λ
1
,
…
,
λ
n
)
\Lambda=\text{diag}(\lambda_1,\dots,\lambda_n)
Λ=diag(λ1?,…,λn?)为特征值对角矩阵。
Laplacian
\text{Laplacian}
Laplacian矩阵的特征分解能够允许在图域上定义等价的傅里叶变换,特征向量对应
Fouries
\text{Fouries}
Fouries的模,特征值对应图上的频率。基于此,令
x
∈
R
n
\textbf{x}\in\mathbb{R}^n
x∈Rn表示定义在图上顶点的信号,那么
x
\textbf{x}
x的图上
Fouries
\text{Fouries}
Fouries变换为
x
^
=
U
?
x
\hat{\textbf{x}}=\textbf{U}^\top\textbf{x}
x^=U?x且逆操作为
x
=
U
x
^
\textbf{x}=\textbf{U}\hat{\textbf{x}}
x=Ux^。因此,信号
x
\textbf{x}
x和过滤器
g
\textbf{g}
g的图卷积操作定义为
g
?
x
=
U
(
(
U
?
g
)
⊙
(
U
?
x
)
)
=
U
G
^
U
?
x
(9)
\textbf{g}*\textbf{x}=\textbf{U}((\textbf{U}^\top\textbf{g})\odot(\textbf{U}^\top\textbf{x}))=\textbf{U}\hat{\textbf{G}}\textbf{U}^\top\textbf{x} \tag{9}
g?x=U((U?g)⊙(U?x))=UG^U?x(9)
其中,
G
^
=
diag
(
g
^
1
,
…
,
g
^
n
)
\hat{\textbf{G}}=\text{diag}(\hat{g}_1,\dots,\hat{g}_n)
G^=diag(g^?1?,…,g^?n?)表示对角矩阵,其对角线元素对应谱过滤器系数。
? 图卷积能够通过
Laplacian
\text{Laplacian}
Laplacian的k阶多项式完成近似,
U
G
^
U
?
x
≈
∑
i
=
0
k
θ
i
Δ
i
x
=
U
(
∑
i
=
0
k
θ
i
Λ
i
)
U
?
x
(10)
\textbf{U}\hat{\textbf{G}}\textbf{U}^\top\textbf{x}\approx\sum_{i=0}^k\theta_i\Delta^i\textbf{x}=\textbf{U}\Big(\sum_{i=0}^k\theta_i\Lambda^i\Big)\textbf{U}^\top\textbf{x} \tag{10}
UG^U?x≈i=0∑k?θi?Δix=U(i=0∑k?θi?Λi)U?x(10)
其中,
θ
i
\theta_i
θi?表示系数。在这个例子中,过滤器系数对应于
Laplacian
\text{Laplacian}
Laplacian特征值的多项式,即
G
^
=
∑
i
θ
i
Λ
i
\hat{\textbf{G}}=\sum_i\theta_i\Lambda^i
G^=∑i?θi?Λi或者相当于
g
^
(
λ
i
)
=
∑
i
θ
i
λ
j
i
\hat{g}(\lambda_i)=\sum_i\theta_i\lambda_j^i
g^?(λi?)=∑i?θi?λji?。
? 图卷积神经网络利用了等式
(
10
)
(10)
(10)的线性近似,该线性近似具有系数
θ
0
=
2
θ
\theta_0=2\theta
θ0?=2θ和
θ
1
=
?
θ
\theta_1=-\theta
θ1?=?θ。得到基本的
GCN
\text{GCN}
GCN卷积操作
g
?
x
=
θ
(
I
+
D
?
1
/
2
AD
?
1
/
2
)
x
(11)
\textbf{g}*\textbf{x}=\theta(\textbf{I}+\textbf{D}^{-1/2}\textbf{AD}^{-1/2})\textbf{x} \tag{11}
g?x=θ(I+D?1/2AD?1/2)x(11)
在其最终的设计中,将矩阵
I
+
D
?
1
/
2
AD
?
1
/
2
\textbf{I}+\textbf{D}^{-1/2}\textbf{AD}^{-1/2}
I+D?1/2AD?1/2替换为规范化版本
D
~
?
1
/
2
A
~
D
~
?
1
/
2
\tilde{\textbf{D}}^{-1/2}\tilde{\textbf{A}}\tilde{\textbf{D}}^{-1/2}
D~?1/2A~D~?1/2,其中
A
~
=
A+I
\tilde{\textbf{A}}=\textbf{A+I}
A~=A+I且
D
~
=
D+I
\tilde{\textbf{D}}=\textbf{D+I}
D~=D+I。
2. SGC \text{SGC} SGC和低通滤波
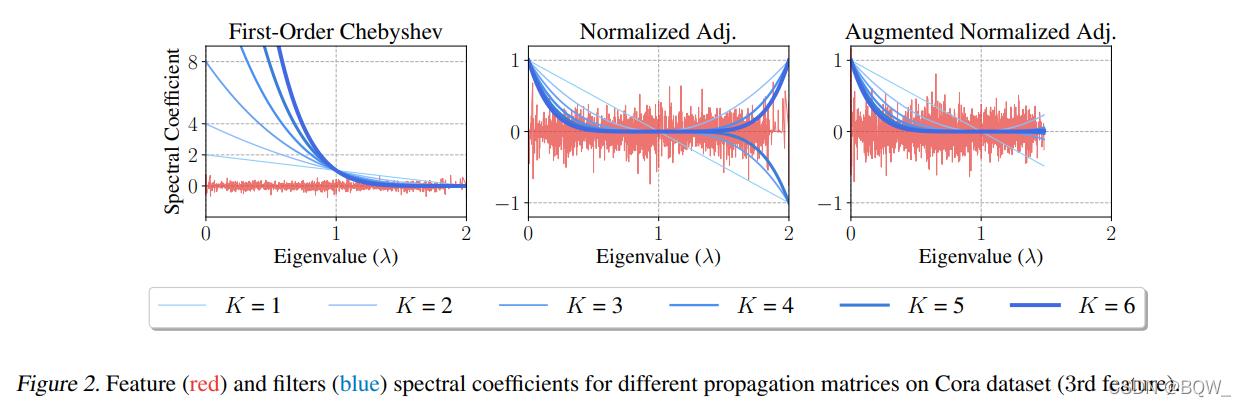
? GCN \text{GCN} GCN中初始的过滤器对应于传播矩阵 S 1-order = I + D ? 1 / 2 A D ? 1 / 2 \textbf{S}_{\text{1-order}}=\textbf{I}+\textbf{D}^{-1/2}\textbf{A}\textbf{D}^{-1/2} S1-order?=I+D?1/2AD?1/2。规范化拉普拉斯算子为 Δ sym = I ? D ? 1 / 2 AD ? 1 / 2 \Delta_{\text{sym}}=\textbf{I}-\textbf{D}^{-1/2}\textbf{AD}^{-1/2} Δsym?=I?D?1/2AD?1/2,那么 S 1-order = 2 I ? Δ sim \textbf{S}_{\text{1-order}}=2\textbf{I}-\Delta_{\text{sim}} S1-order?=2I?Δsim?。因此,特征传播 S 1-order K \textbf{S}_{\text{1-order}}^K S1-orderK?意味着过滤系数 g ^ i = g ^ ( λ i ) = ( 2 ? λ i ) K \hat{g}_i=\hat{g}(\lambda_i)=(2-\lambda_i)^K g^?i?=g^?(λi?)=(2?λi?)K,其中 λ i \lambda_i λi?表示 Δ sym \Delta_{\text{sym}} Δsym?的特征值。上图展示了传播步骤 K ∈ { 1 , … , 6 } K\in \{1,\dots,6\} K∈{1,…,6}的变化与 S 1-order \textbf{S}_{\text{1-order}} S1-order?过滤操作的关系。可以观察到,高阶 S 1-order \textbf{S}_{\text{1-order}} S1-order?将会导致过滤系数的爆炸并在频率 λ i < 1 \lambda_i<1 λi?<1上过度放大。
? 为了解决一阶过滤器的问题, Kipf&Welling \text{Kipf\&Welling} Kipf&Welling等人提出了 renormalization?trick \text{renormalization trick} renormalization?trick。该方法通过为所有节点加入自循环后的归一化邻接矩阵来替换 S 1-order \textbf{S}_{\text{1-order}} S1-order?。本文称得到的传播矩阵为增强的归一化邻接矩阵 S ~ a d j = D ~ ? 1 / 2 A ~ D ~ ? 1 / 2 \tilde{\textbf{S}}_{adj}=\tilde{\textbf{D}}^{-1/2}\tilde{\textbf{A}}\tilde{\textbf{D}}^{-1/2} S~adj?=D~?1/2A~D~?1/2,其中 A ~ = A+I \tilde{\textbf{A}}=\textbf{A+I} A~=A+I且 D ~ = D+I \tilde{\textbf{D}}=\textbf{D+I} D~=D+I。相应的,定义增强规范化 Laplacian \text{Laplacian} Laplacian矩阵 Δ ~ s y m = I ? D ~ ? 1 / 2 A ~ D ~ ? 1 / 2 \tilde{\Delta}_{sym}=\textbf{I}-\tilde{\textbf{D}}^{-1/2}\tilde{\textbf{A}}\tilde{\textbf{D}}^{-1/2} Δ~sym?=I?D~?1/2A~D~?1/2。这样,就可以将关于 S ~ a d j \tilde{\textbf{S}}_{adj} S~adj?的谱过滤器描述为 Laplacian \text{Laplacian} Laplacian矩阵特征值的多项式,即 g ^ ( λ ~ i ) = ( 1 ? λ ~ i ) K \hat{g}(\tilde{\lambda}_i)=(1-\tilde{\lambda}_i)^K g^?(λ~i?)=(1?λ~i?)K,其中 λ ~ i \tilde{\lambda}_i λ~i?是 Δ ~ s y m \tilde{\Delta}_{sym} Δ~sym?的特征值。
-
定理1
令 A \textbf{A} A是一个无向、有权且无孤立点的简单图的邻接矩阵,其对应的度矩阵为 D \textbf{D} D。令 A ~ = A + γ I \tilde{\textbf{A}}=\textbf{A}+\gamma\textbf{I} A~=A+γI为增强邻接矩阵( γ > 0 \gamma>0 γ>0),其对应的度矩阵为 D ~ \tilde{\textbf{D}} D~。令 λ 1 \lambda_1 λ1?和 λ n \lambda_n λn?表示 Δ s y m = I ? D ? 1 / 2 AD ? 1 / 2 \Delta_{sym}=\textbf{I}-\textbf{D}^{-1/2}\textbf{AD}^{-1/2} Δsym?=I?D?1/2AD?1/2的最小特征这和最大特征值。类似地, λ ~ 1 \tilde{\lambda}_1 λ~1?和 λ ~ n \tilde{\lambda}_n λ~n?则是 Δ ~ s y m = I ? D ~ ? 1 / 2 A ~ D ~ ? 1 / 2 \tilde{\Delta}_{sym}=\textbf{I}-\tilde{\textbf{D}}^{-1/2}\tilde{\textbf{A}}\tilde{\textbf{D}}^{-1/2} Δ~sym?=I?D~?1/2A~D~?1/2的最小特征性和最大特征值。则有
0 = λ 1 = λ ~ 1 < λ ~ n < λ n (12) 0=\lambda_1=\tilde{\lambda}_1<\tilde{\lambda}_n<\lambda_n \tag{12} 0=λ1?=λ~1?<λ~n?<λn?(12)
定理1表明,在加入自循环 γ > 0 \gamma>0 γ>0后,规划化 Laplacian \text{Laplacian} Laplacian矩阵的最大值变小。