文章目录
3 灰度变换与空间滤波
3.1 图像处理
3.1.1 图像处理增强
增强的首要目标是处理图像,使其比原始图像更适合与特定应用。
“特定”:适合X光成像的处理,突出骨骼、肌肉,不适合于“磨皮”。
图像增强的方法分为两大类: 空间域方法和频域方法。
- 空间域:指图像平面自身,这类方法是以对图像 的像素直接处理为基础的
- 频域处理技术是以修改图像的傅氏变换为基础的
3.2 某些基本灰度变换
**s = T(r)**表达式的函数T是把像素值 r 映射到值 s 的一种变换。
由于处理的数字量,变换函数的值通常存储在一个一维矩阵中,并且通过查表得到映射。
对于 8 比特环境,一个包含 T 值的可查阅的表需要有256个记录,称为:查找表 LUT(Look Up Table)
图像增城常用的三个基本类型函数: 线性的(正比和反比)、对数的(对数和反对数变换)、幂次的(n次幂和n次方根变换)
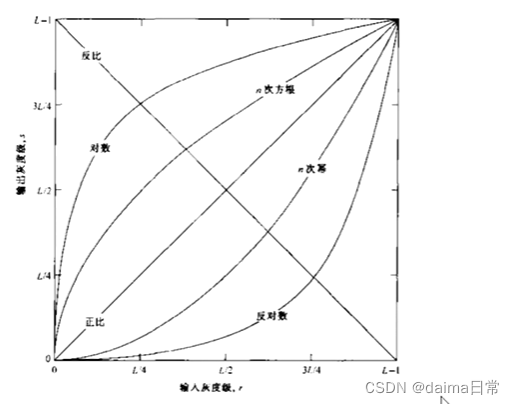
图1 用于图像增强的某些基本灰度变换函数
3.2.1 图像翻转
灰度级范围为 [0,L-1] 的图像翻转表达式为 (黑白底片的照片)
s = L -1 -r
3.2.2 对数变换(动态范围扩散/压缩)
对数变换的一般表达式为:
s = clog(1+r),其中c是常数,并假设 c >= 0
(加1的目的:防止对数真值部分出现0,s等于负无穷现象)
对数使一个窄带低灰度输出图像值映射为一个宽带输出值,
- 大部分原图中的低灰度像素结果映射灰度值集中在高亮区域
- 将原理很大动态范围的 r 转换为动态范围很小的 s
典型例子就是傅里叶频谱,它的像素值有很大的动态范围。
- 当计算机处理像这样的大数字时,图像显示系统通常不能如实第再现如此大范围的强度值
- 最后的效果是有很多的细节会在典型的傅里叶频谱显示时丢失
- 利用对数变换调整后的图像的细节可见程度更好
3.2.3 幂次(伽马)变换
1、幂次变换的基本形式
s = cr^γ,其中 c 和 γ为正常数。
如对数变换的情况一样, γ < 1的幂次曲线把输入窄带暗值映射到宽带输出值。
- γ > 1的曲线 和 γ < 1 的曲线有相反的效果
- 当 c = γ = 1时,将退化为正比变换
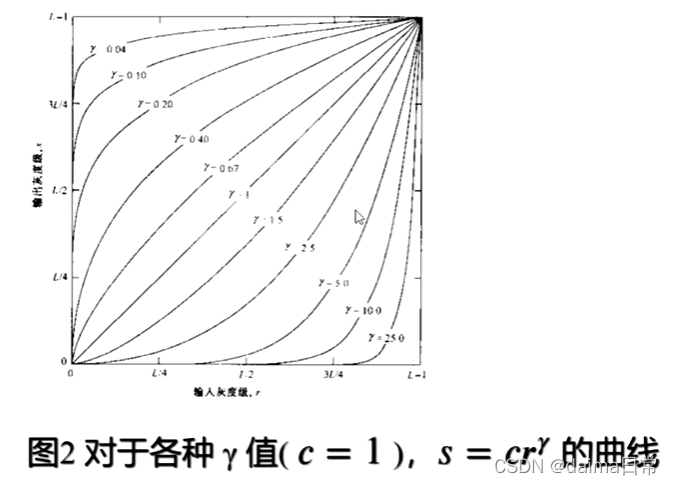
2、幂次变换用于伽马校正
用于图像获取、打印和显示的各种装置根据幂次规律进行响应。用于修正幂次响应现象的过程称为伽马校正。
例如:阴极射线管(CRT)显示的校正
3、幂次变换用于对比度增强
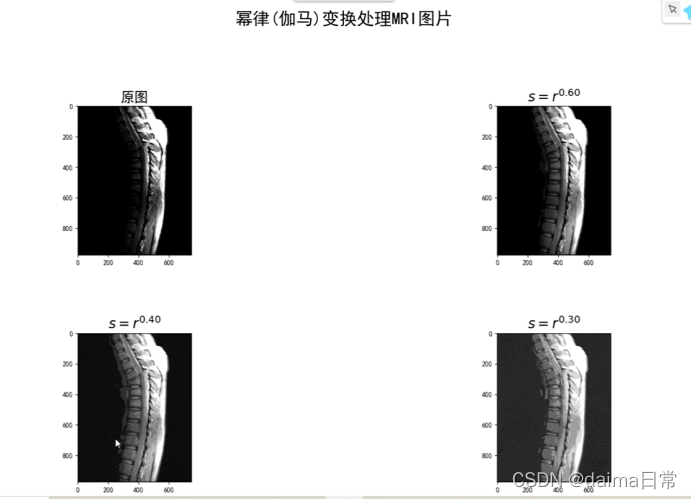
压缩灰度级:γ > 1

问:对数、幂次,从效果上来讲,有太大区别吗?
答:没有太大的区别
按对比线性拉伸可以将原始输入图像中的灰度值不加区别地扩展
3.2.4 分段线性变换函数
按比例线性拉伸可以将原始输入图像中的灰度值不加区别地扩展
实际应用中,为了突出图像中感兴趣的研究对象,常常
- 要求局部扩展拉伸某一范围的灰度值
- 对不同范围的灰度值进行不同的拉伸处理即分段性拉伸
一般来讲,分段线性拉伸实际是
- 仅将某一范围的灰度值进行拉伸
- 其余范围的灰度值实际上是被压缩了
优点:可以任意组合需要的形式,可以用线性函数拟合对数函数
缺点:其需要更多的用户输入
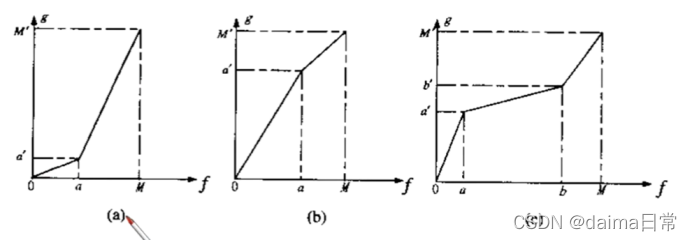
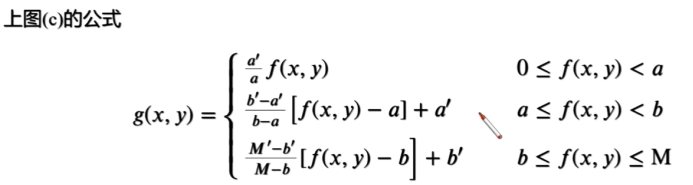
1、 对比拉伸
照明不足、成像传感器动态范围太小,甚至在图像获取过程中透镜光圈设置错误,产生低对比图像。对比拉伸的思想是提高图像处理时灰度级的动态范围。

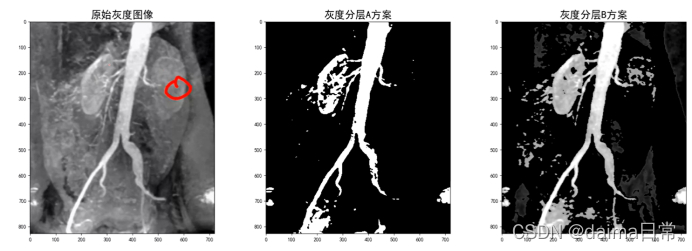
2、灰度切割
提高特定灰度范围的亮度。应用包括增强特征(如卫星图像中大量的水)和增强x射线图中的缺陷 p69
两种基本方法:
- 为关心的范围内所有灰度指定一个较高值,而为其他灰度指定一个较低值。如 p68变换产生二进制图像
- 使所需范围的灰度变亮,但是仍保持了图像的背景和灰度色调
3、位图切割/比特平面分层 p84
不提高灰度范围的亮度,而提高对特定位提高亮度
8 比特图像由 8个比特平面(低有效应的位平面0 ~ 高有效位的位平面7)组成
- 平面 0 包含像素的最低位,平面 7 包含最高位
- 较高阶位(特别是前四位)包含了多数在视觉上很重要的数据,其他位对微小细节有作用。
把数字图像分解成为位平面,对于分析每一个位在图像中的相对重要性是有用的,这种分解在第 8 章所讨论的图像压缩中很有用。


3.3 直方图的处理(必考)
灰度级为 [ 0,L - 1]范围的数字图像的直方图是离散函数 h(rk)= nk ,这里 rk是第k级灰度,nk是图像中灰度级为 rk 的像素个数。
以图像中像素的总数(用 n 表示)来除它的每一个值得到归一化的直方图(normalized histogram)
归一化的直方图由 P(rk)=nk/n给出,这里 k = 0,1,2…,L-1。
或者说数字图像的直方图定义为一个离散函数,它表示数字图像中每一灰度级与其出现概率的统计关系:
- p(rk)给出了灰度级为 rk 发生的概率估计值
- 归一化的直方图其所有部分之和是 1
3.3.0 基本图像类型与直方图的对应关系
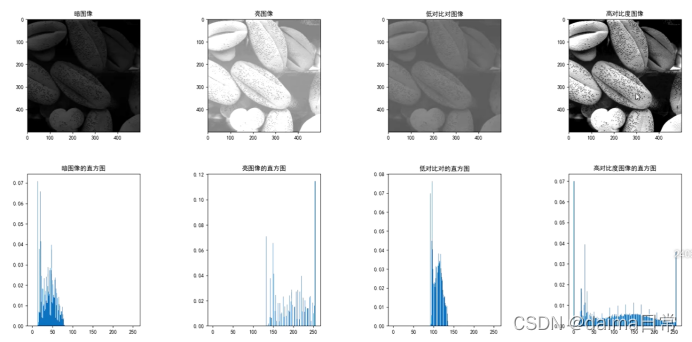
由上图可总结得到四个基本灰度级特征(暗、亮、低对比度和高对比度)
- 暗色图像中,直方图的组成成分集中在灰度级低(暗)的一侧
- 高亮图像中,直方图的组成成分集中在灰度级高(亮)的一侧
- 低对比度图像的直方图窄而集中于灰度级的中部
- 高对比度的图像中,直方图的成分覆盖了灰度级很宽的范围,而且像素的分布相对均匀,只有少量垂线比其他的高许多。
结论:
若一幅图像其像素占有全部可能的灰度级并且分布均匀,则这样的图像
- 有高对比度和多变的灰度色调
- 是一幅灰度级丰富且大豆肽范围大的图像
3.3.1 直方图均衡化 p72
s = T(r),0 <= r <= L-1 (0–黑,L-1----白)
假设变化函数 T 满足下列条件:
(a)、T(r)在区间 0 <= r <= L-1中为严格单调递增函数
如何为严格递增函数:
-
若 r2 > r1,则 T(r2)=> T(r1):T为单调递增函数
-
若 r2 > r1,则 T(r2)> T(r1):T为严格单调递增函数
(b)、当0 <= r <= L-1时, 0 <= T? <= L-1
**条件(a)**中要求T?为严格单调递增函数,是保证反变换存在,单调条件保持输出图像从黑到白顺序增加。不会函数不单调增加将导致至少有一部分亮度范围被颠倒,从而输出图像中产生一下反转灰度级
**条件(b)**保证输出灰度级与输入有相同的范围。
由s到r的反变换可以表示为:
r = T^(-1)(s),其中s 为自变量 0 <= s <= L-1
图像的灰度可以被视为区间 [0,L-1] 随机变量,可用概论密度函数PDF(Probability Distribution Function)描述
1、连续值
令 Pr(r)和Ps(s)分别代表随机变量 r 和 s 的概论密度函数,如果T?连续且在定义域内可微,则由概率论知识推导得到
Ps(s)Pr(r)|dr / ds|
及变换变量 s 的概论密度函数有输入图像的灰度级 PDF和所选择的变换函数决定。


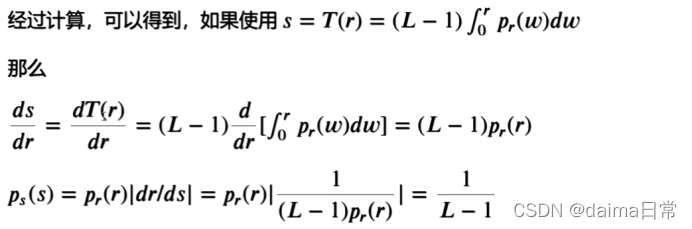
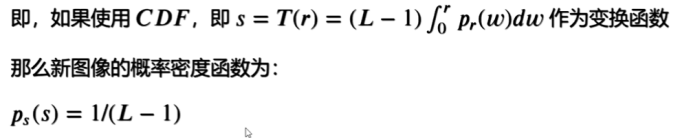
结论:
- CDF会得到以随机变量,其特征为均匀概论密度函数
- CDF 得到的 s PDF始终是均匀的,与Pr(r)的形式无关

2、离散值

这个变换(映射)称为直方图均衡化或者直方图线性化,它同时满足条件(a)和(b)
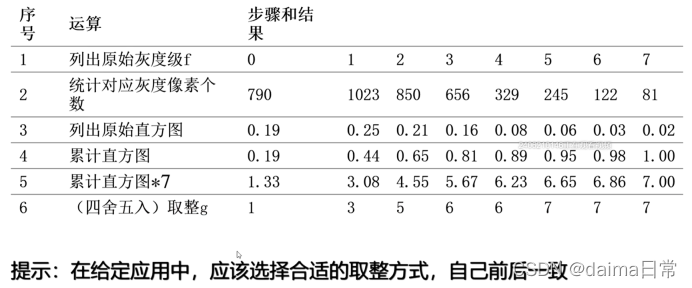

与连续形式不同:
- 一般不能证明离散变换能产生均匀概论密度函数的离散值
- 均衡化有展开输入图像直方图的趋势,以至于直方图均衡化过的图像灰度级能跨越较大的范围
- 直方图均衡化一般会使原始图像 的灰度等级减少,这是由于均衡化过程要进行近似合入所造成的,被合并的灰度级是原始图像上出现频率较低的灰度级
- 若这些灰度级构成的图像细节比较重要
- 采用局部自适应的直方图均衡化技术
- 用增加像素位数的方法减少由于灰度级简并造成的灰度层次的损失
例3 P75 :处理对象:利用不同变换函数(P76)得到不同对比度的图
直方图均衡化在第四幅图像中没有在视觉上产生重要不同,这是因为这幅图像的直方图已扩展了全部灰度级范围
直方图均衡化后的图像本身在视觉上很相似,这是因为左侧的一列图像之间的差异仅仅是一种简单对比,而不是内容上的。也就是说,因为图像有系统的内容,从直方图均衡化导致的对比增强足以使得结果图像中,在视觉上难以区分灰度级的差别。

注意:(学习过程中最怕就是提不出问题,要自己去问自己为什么是这样的)
高调摄影 High-key photography
- 明亮和高光以白色为主
- 非常小的黑色和中间色调
- 视觉上营造出乐观,年轻,轻盈,通风的感觉
- 这种能够很有效的消除皱纹和毛孔;多用于肖像,婚礼,新生儿和时尚摄影

低调摄影 Low-key photography
- 使用大量深黑色,深色调和阴影
- 非常少量的白色和中间色调减少光照
- 以产生具有鲜明对比的图像
- 能创作出戏剧性和神秘的照片

3.3.2 直方图匹配(规定化)
直方图均衡化能自动地确定变换函数,该函数力求产生均匀直方图的输出图像,当需要自动增强时
有时希望可以指定处理的图像所具有的直方图形状,这种用于生产处理后有特殊直方图的图像的方法,叫做直方图匹配或直方图规定化处理
遥感数字图像处理中常用直方图规定化,其目的并不是为了直接去增强一幅图像,而是为了使一幅图像与另一幅(相邻)图像的色调尽可能保持一致,一般称为直方图匹配,即以目标(参考)图像的直方图为参考对象,调整另一幅图像的直方图,使之尽可能与目标图像保持一致。例如,在进行两幅图像的镶嵌(拼接)时,由于两幅图像的时节不同会引起图像间色调差异,这就需要在镶嵌前进行直方图匹配,使两幅图像的色调尽可能保持一致,做到无缝拼接。
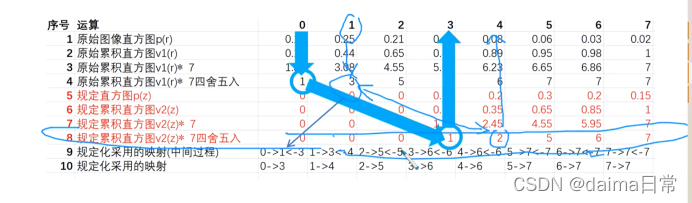
实际应用:
