[人工智能]机器学习之朴素贝叶斯模型

朴素贝叶斯

1、什么是朴素贝叶斯算法

（1）字面理解：朴素贝叶斯 = “朴素”+贝叶斯

朴素：假定特征之间都是条件独立的(这里理解起来比较抽象，后续使用具体实例说明)

贝叶斯：贝叶斯定理
$$\begin{gathered} p(y|x)=\frac{p(x|y)?p(y)}{p(x)} \\ 证明：p(x,y)=p(x|y)?p(y)=p(y|x)?p(x) \\ 移项得：p(y|x)=\frac{p(x|y)?p(y)}{p(x)} \end{gathered}$$
说明：

1）p(y|x)：后验概率

2）p(x|y)：似然概率

3）p(y)：先验概率

4）p(x):样本数据的所有特征

（2）官方解释：朴素贝叶斯分类（NBC）是以贝叶斯定理为基础并且假设特征条件之间相互独立的方法，先通过已给定的训练集，以特征词之间独立作为前提假设，学习从输入到输出的联合概率分布，再基于学习到的模型，输入X求出使得后验概率最大的输出Y。(来自于百度百科)

2、朴素贝叶斯的应用

1）各类文本分析的任务，比如垃圾邮件的分类，文本主题分类，情感分析

2）文字识别

3）图像识别

3、使用朴素贝叶斯对垃圾邮件进行分类

这里用一个具体的实例来分享朴素贝叶斯模型，能够更直观的理解朴素贝叶斯模型

3.1、朴素贝叶斯对垃圾邮件分类的两个步骤

1）统计出每一个单词对一个邮件成为垃圾邮件或正常邮件的概率

2）用这些统计的结果对一个新的邮件做预测

3.2、实现

1）例：现若干邮件，其中有正常邮件，有垃圾邮件，邮件中出现了”购买“，”物品“，”不是“，”广告“，”这“等词…我们分别统计这些词出现在正常邮件中的个数，出现在垃圾邮件中的个数

则正常邮件含有”购买“，”物品“，”不是“，”广告“，”这“词的概率为
$$\begin{array}{rl}p(购买|正常邮件)& =\frac{1}{80}\\ p(物品|正常邮件)& =\frac{1}{60}\\ p(不是|正常邮件)& =\frac{1}{60}\\ p(广告|正常邮件)& =\frac{1}{48}\\ p(这|正常邮件)& =\frac{1}{80}\\ p(正常)& =\frac{2}{3}(分子：所有邮件中正常邮件的个数；分母：邮件的总数)\end{array}$$
垃圾邮件含有”购买“，”物品“，”不是“，”广告“，”这“词的概率为
$$\begin{array}{rl}p(购买|垃圾邮件)& =\frac{7}{120}\\ p(物品|垃圾邮件)& =\frac{1}{30}\\ p(不是|垃圾邮件)& =\frac{1}{40}\\ p(广告|垃圾邮件)& =\frac{1}{30}\\ p(这|垃圾邮件)& =0\\ p(正常)& =\frac{2}{3}(分子：所有邮件中垃圾邮件的个数；分母：邮件的总数)\end{array}$$
收到了新的一份邮件E（购买物品这不是广告），属于垃圾邮件还是正常邮件？
$$\begin{array}{rl}p(E|正常邮件)& =\frac{p(购买，物品，这，不是，广告|正常邮件)?p(正常邮件)}{p(邮件内容)}\\ & =\frac{p(购买|正常邮件)?p(物品|正常邮件)?p(这|正常邮件)?p(不是|正常邮件)?p(广告|正常邮件)?p(正常邮件)}{p(邮件内容)}(在这里我们把联合概率转换成了条件概率，前提就是一开始我提到的“朴素”，如果没有这个条件，两式是不能划等号的)\\ & =\frac{\frac{1}{80}?\frac{1}{60}?\frac{1}{80}?\frac{1}{60}?\frac{1}{48}?\frac{2}{3}}{p(邮件内容)}\\ p(E|垃圾邮件)& =\frac{p(购买，物品，这，不是，广告|垃圾邮件)?p(垃圾邮件)}{p(邮件内容)}\\ & =\frac{p(购买|垃圾邮件)?p(物品|垃圾邮件)?p(这|垃圾邮件)?p(不是|垃圾邮件)?p(广告|垃圾邮件)?p(垃圾邮件)}{p(邮件内容)}\\ & =\frac{\frac{7}{120}?\frac{1}{30}?0?\frac{1}{40}?\frac{1}{30}?\frac{1}{3}}{p(邮件内容)}\end{array}$$
通过上面的计算，我们可以看到分母相同的情况下P(E|正常邮件)明显大于P(E|垃圾邮件)=0，大家认为这个结论合理嘛？明显是不合理的，原因是或许邮件包含某个垃圾邮件的关键词，但这封邮件并不一定是垃圾邮件，同理正常邮件也是如此，导致这个问题的罪魁祸首就是某个关键词的条件概率为0，如何解决这个问题呢？答案就是采用平滑

2）什么是平滑？不说废话直接上公式
$$\begin{gathered} p(w|y=c)=\frac{语料库中的单词w出现的次数+1}{类别为c的语料库中包含所有的单词个数+v} \\ v:词典的大小 \end{gathered}$$
这里分母为什么要加v(词典的大小)？

答：为了让每一个词的条件概率最终相加为1，假设有一个词库v=[a,b,c,d,…]^T(T:转置),

则p(a|y=c)+p(b|y=c)+p(c|y=c)+p(d|y=c)+… = 1

3）现在有一个新的需求：

①垃圾邮件，包含8个词

（1）点击 更多 信息

（2）最新 产品

（3）信息 点击 链接

②正常邮件，包含 6个词

（1）开会

（2）信息 详见 邮件

（3）最新 信息

新邮件：S = 最新 产品 点击 链接 产品

新邮件S是垃圾邮件还是正常邮件?

建立词库v={点击，更多，信息，最新，产品，链接，开会，详见，邮件}

单词数量n=9
$$\begin{array}{rl}p(点击|正常邮件)& =\frac{0+1}{6+9}\\ p(更多|正常邮件)& =\frac{0+1}{6+9}\\ p(信息|正常邮件)& =\frac{2+1}{6+9}\\ p(最新|正常邮件)& =\frac{1+1}{6+9}\\ p(产品|正常邮件)& =\frac{0+1}{6+9}\\ p(链接|正常邮件)& =\frac{0+1}{6+9}\\ p(开会|正常邮件)& =\frac{1+1}{6+9}\\ p(详见|正常邮件)& =\frac{1+1}{6+9}\\ p(邮件|正常邮件)& =\frac{1+1}{6+9}\\ p(正常邮件)=\frac{1}{2}& \end{array}$$

$$\begin{array}{rl}p(点击|垃圾邮件)& =\frac{2+1}{8+9}\\ p(更多|垃圾邮件)& =\frac{1+1}{8+9}\\ p(信息|垃圾邮件)& =\frac{2+1}{8+9}\\ p(最新|垃圾邮件)& =\frac{1+1}{8+9}\\ p(产品|垃圾邮件)& =\frac{1+1}{8+9}\\ p(链接|垃圾邮件)& =\frac{1+1}{8+9}\\ p(开会|垃圾邮件)& =\frac{0+1}{8+9}\\ p(详见|垃圾邮件)& =\frac{0+1}{8+9}\\ p(邮件|垃圾邮件)& =\frac{0+1}{8+9}\\ p(垃圾邮件)=\frac{1}{2}& \end{array}$$

在上述计算词库中每个词的条件概率，使用加1平滑后，分母加词库的大小n=9，使P(v|正常邮件)=1；P(v|垃圾邮件)=1，可以加加看！
$$\begin{array}{rl}p(S|正常邮件)& =\frac{p(最新,产品,点击,链接,产品|正常邮件)?p(正常邮件)}{p(邮件内容)}\\ & =\frac{p(最新|正常邮件)?p(产品|正常邮件)?p(点击|正常邮件)?p(链接|正常邮件)?p(产品|正常邮件)?p(正常邮件)}{p(邮件内容)}\\ & =\frac{\frac{2}{15}?\frac{1}{15}?\frac{1}{15}?\frac{1}{15}?\frac{1}{15}?\frac{1}{2}}{p(邮件内容)}\\ p(S|垃圾邮件)& =\frac{p(最新,产品,点击,链接,产品|垃圾邮件)?p(正常邮件)}{p(邮件内容)}\\ & =\frac{p(最新|垃圾邮件)?p(产品|垃圾邮件)?p(点击|垃圾邮件)?p(链接|垃圾邮件)?p(产品|垃圾邮件)?p(垃圾邮件)}{p(邮件内容)}\\ & =\frac{\frac{2}{17}?\frac{2}{17}?\frac{3}{17}?\frac{2}{17}?\frac{2}{17}?\frac{1}{2}}{p(邮件内容)}\end{array}$$
最后我们得出：

因为p(S|正常邮件)<p(S|垃圾邮件)，所以S为垃圾邮件的可能性会更大

**Tips：我们可以看到上述计算出的条件概率非常小，在计算机中容易出现”溢出的现象“，为了避免该问题我们加入log，这样log(p1 p2 p3) = logp1+logp2+log3，我就不在这里过多的赘述了！

4、朴素贝叶斯的最大似然估计

4.1、预备知识

1）最大似然估计：

最大似然的核心：假设未知参数为θ，已知的样本为D，最大似然估计通过最大化P(D|θ)来求解未知参数θ

最大似然估计的详细解释我在逻辑回归一文中做了详细阐述，就不过多赘述

2）带限制条件的优化

①无约束条件的优化：
$$\begin{array}{r}例1.求f(x)=x^2?2x?3的最小值\\ 解：f^{{}^{\prime }}(x)=2x?2\\ 令f^{{}^{\prime }}(x)=0\\ 得x=1\end{array}$$
②带约束条件的优化-拉格朗日惩罚项
$$\begin{gathered} 求f(x,y)=x+y的最大值，但有个条件是x^2+y^2=1 \\ 解:由x^2+y^2=1 \\ 得x^2+y^2?1=0 \\ 设f(x,y,\lambda )=x+y+\lambda (x^2+y^2?1) \\ ?\begin{array}{l}{f}_x^{{}^{\prime }}(x,y,\lambda )=1+2\lambda x=0\\ f_y^{{}^{\prime }}(x,y,\lambda )=1+2\lambda y=0\\ f_{\lambda }^{{}^{\prime }}(x,y,\lambda )=x^2+y^2?1=0\end{array} \\ 得：?\begin{array}{l}{\lambda }_1=\frac{\sqrt{2}}{2}\\ x_1=?\frac{\sqrt{2}}{2}\\ y_1=?\frac{\sqrt{2}}{2}\end{array}?\begin{array}{l}{\lambda }_2=?\frac{\sqrt{2}}{2}\\ x_2=\frac{\sqrt{2}}{2}\\ y_2=\frac{\sqrt{2}}{2}\end{array} \\ 综上：得令f(x,y)=x+y最大的值为 \\ ?\begin{array}{l}{\lambda }_2=?\frac{\sqrt{2}}{2}\\ x_2=\frac{\sqrt{2}}{2}\\ y_2=\frac{\sqrt{2}}{2}\end{array} \end{gathered}$$

4.2、得到朴素贝叶斯的目标函数

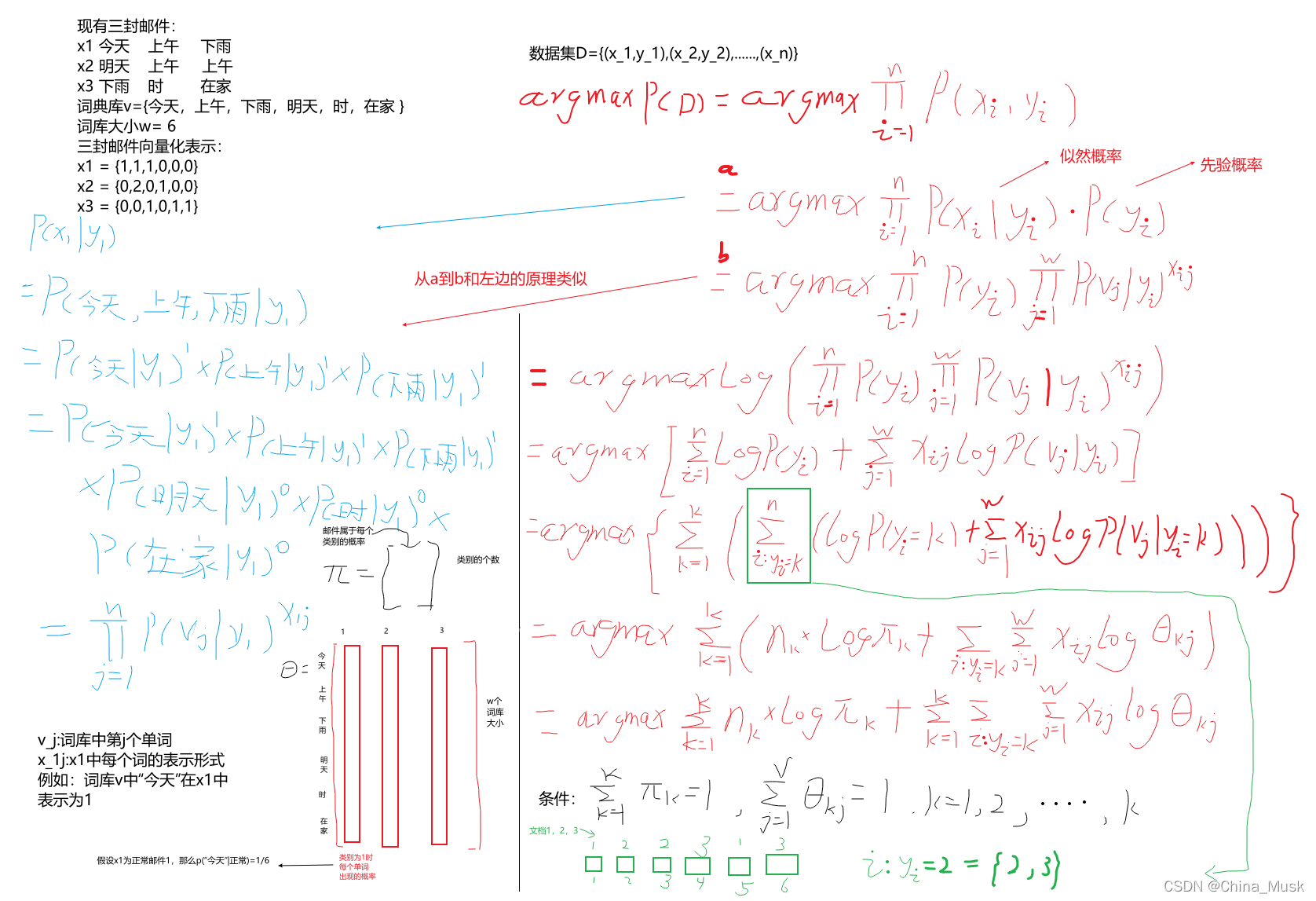
4.3、对目标函数的求解