1.1数学优化
形如:
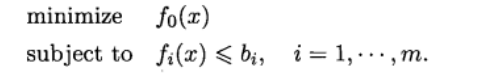
向量x =(x1…xn)称为问题的优化变量,
函数fxo∶Rn→R称为目标函数,
函数fi:R →R, i= 1,.… , m,称为(不等式)约束函数
常数 b1,…, bm称为约束上限或者约束边界。
对于任意满足约束fi(z)≤b1,…, fm(z)≤bm的向量z,有fo(z)≥ fo(a*),那么称*为问题(1.1)的最优解或者解。
线性优化:
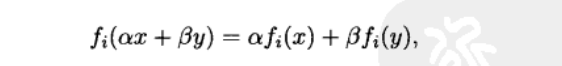
凸优化:(α>0,β>0,且α+β+1)
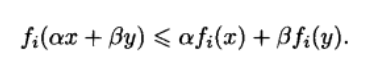
结论:线性优化条件更为苛刻,凸优化可以看作是线性优化的一种扩展。
凸优化的应用:
1.投资组合优化
2.器件尺寸问题
优化问题可以看成在向量空间Rn的一集备选解中选择最好的解。用x表示备选解,fi(x)≤b表示 x 必须满足的条件,目标函数fo(x)表示选择x的成本(同理也可以认为—fo(a)表示选择α 的效益或者效用)。优化问题的解即为满足约束条件的所有备选解中成本最小(或者效用最大)的那个解。
3.数据拟合
在数据拟合中,我们通常需要选择一个模型,而变量则是模型的参数,所以需要解决的问题就是寻找合适的模型参数,使得与真实模型之间偏差达到预期值(偏差最小值)。
1.2最小二乘法与线性规划
最小二乘问题:
没有约束条件(m=0),目标函数是若干项平方和。每一项都有具体的形式: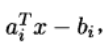
公式如下:
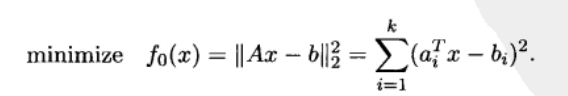
其中,A ∈ R的k×n次方(k ≥n),ai的转置是矩阵A的行向量,向量x∈ Rn是优化变量。
其中最小二乘问题的求解可以化成一组线性方程:
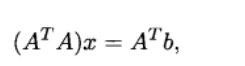
优化变量x=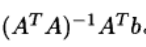
最小二乘应用:
判断一个优化问题是否是最小二乘问题方法:看目标函数是否为二次函数,然后检验函数是否是半正定函数。
加权最小二乘本: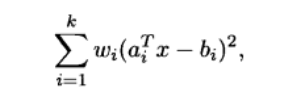
其中加权系数w均大于0.加权系数反应求和项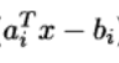
的重要程度。
正则化优化:
正则化是解决最小二乘问题的另一个技术,它通过在成本函数中增加一些多余的项来实现。一个最简单的形式是在成本函数中增加一项和变量平方和成正比的项

线性规划:
另一类较为重要的优化问题是线性规划,其目标函数和所有的约束函数均为线性函数,线性规划问题可以表述如下:
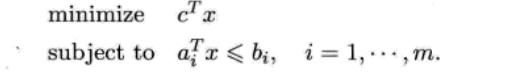
Chebyshev逼近问题
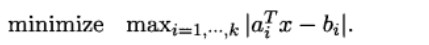
其中,优化变量a ∈ Rn,a1,…“,ak ∈ R”。b1,…,by ∈R为问题的参数,参数取值确定后即得到了一个具体问题。我们注意到,此问题与最小二乘问题式有着一定的相似性。对于这两个问题,目标函数中均含有ai的转置 - bi。不同的是,在最小二乘问题中,我们采用ai的转置 - bi的平方和作为目标函数,而在Chebyshev逼近问题中,我们优化ai的转置 - bi的绝对值中最大的一项。另外一个重要差别在于Chebyshev逼近问题式中的目标函数是不可微的;而最小二乘问题式中的目标函数是二次的,自然也是可微的。
可以等价为线性规划:
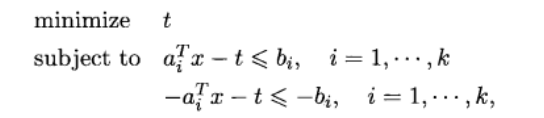
1.3凸优化
形如:
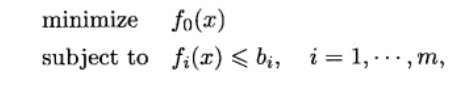
其中,函数fo,…,fm : Rn→R为凸函数。即对于任意x,y ∈ Rn,a,β ∈R且α +β = 1,α ≥ 0,β≥0,这些函数满足
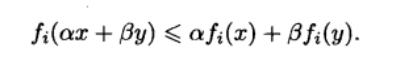
求解凸优化问题
凸优化问题的解并没有一个解析表达式,但是,和线性规划问题类似,存在很多有效的算法求解凸优化问题。在实际应用中,内点法就较为有效,在一些情况下,可以证明,内点法可以在多项式时间内以给定精度求解这些凸优化问题。
在凸优化问题中,每一步需要操作次数与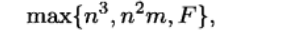 成正比
成正比
其中F是计算目标函数和约束函数fo;… ,fm的一阶导数和二阶导数所需要的计算量。
其他优化:
非线性优化:目标函数或者约束函数是非线性的,对于一般的非线性规划问题是很难解决的,即使变量个数很少,也很难求解;
局部优化:放宽对最优解的要求,寻找局部最优解,只保证在其小领域的所有可行解是目标函数最小,不保证在此领域的其他可行解。然而,除了(可能)不能找到全局最优解以外,局部优化方法还存在一些别的缺点。在局部优化中,需要确定优化变量的初始值,而初始值的选取非常重要,对最终得到的局部最优解有着很大的影响。而且,人们无法估计局部最优解相比(全局)最优解到底有多大的差距。此外,局部优化方法对算法的参数值一般也较为敏感,通常需要针对某个具体的问题或某类问题进行调整。
全局优化:致力于搜索全局最优解,代价则是效率,可能求解的复杂性随着n和m呈指数型增长,因此在变量个数少以及对时间要求不苛刻的问题中可以使用全局优化
非凸优化中的凸优化应用:
1.局部优化中利用凸优化进行初始值的选取
2.非凸优化中的凸启发式算法
3.全局优化的界:对于非凸问题的全局优化,很多方法都需要给出最优解的下界,而且计算代价必须较小。求解下界的两个标准方法都是基于凸优化。在松弛算法中,每个非凸约束都用一个松弛的凸约束代替。在 Lagrange松弛中,我们求解Lagrange对偶问题。此问题是凸的,并给出了原非凸问题最优解的一个下界。