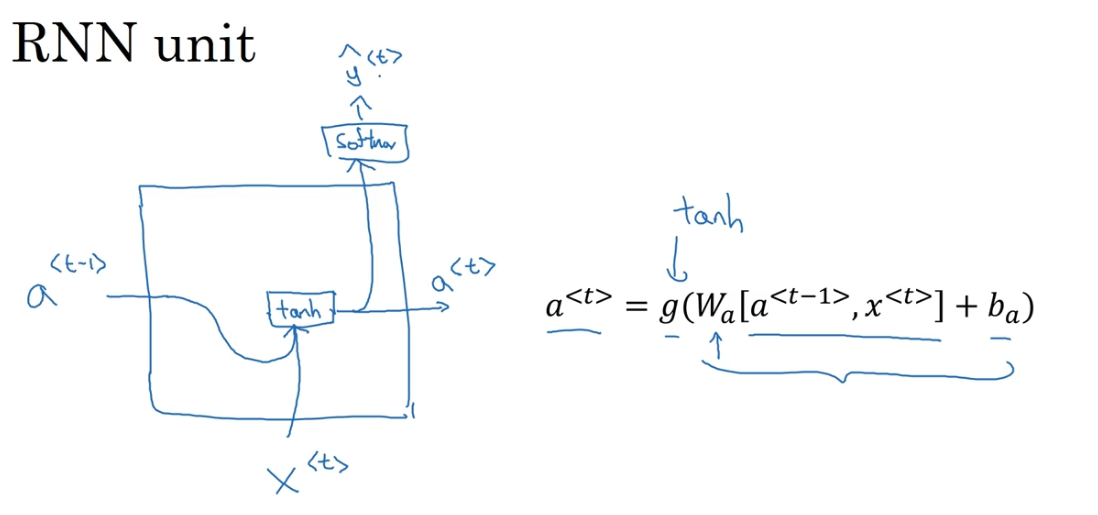
GRU和LSTM
LSTM与GRU的存在是为了解决简单RNN面临的长期依赖问题(由于反向传播存在的梯度消失或爆炸问题,简单RNN很难建模长距离的依赖关系),一种比较有效的方案是在RNN基础上引入门控机制来控制信息的传播。
更通俗地说,比如很长一句话,靠后的某个词和靠前的某个词存在某种关联,简单RNN模型很难把这个靠前的这个词的信息传递到后面
GRU门控循环单元
他能够让你可以在序列中学习非常深的连接
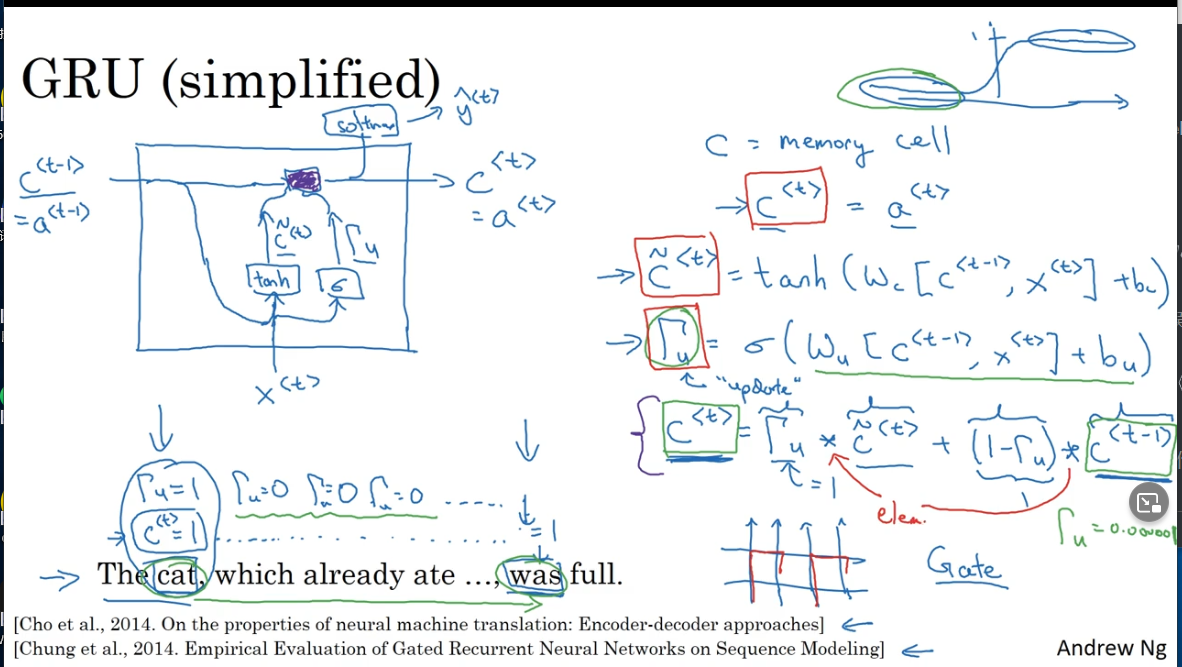
GRU相当于LSTM的简化版
基本原理
- 引入两个信息控制门
Γ u = σ ( ω u [ c ? t ? 1 ? , x ? t ? ] + b u ) \Gamma_{u}=\sigma\left(\omega_{u}\left[c^{\langle t-1\rangle}, x^{\langle t\rangle}\right]+b_{u}\right) Γu?=σ(ωu?[c?t?1?,x?t?]+bu?)
Γ r = σ ( ω u [ c ? t ? 1 ? , x ? t ? ] + b u ) \Gamma_{r}=\sigma\left(\omega_{u}\left[ {c^{\langle t-1\rangle}}, x^{\langle t\rangle}\right]+b_{u}\right) Γr?=σ(ωu?[c?t?1?,x?t?]+bu?)
(1) 更新门 Γ u \Gamma_{u} Γu? : 控制当前状态 c t c^t ct需要从上一时刻状态 c t ? 1 c^{t-1} ct?1中保留多少信息,以及需要从候选状态 c ~ ( t ) \tilde{\boldsymbol{c}}^{(t)} c~(t)中接收多少信息
(2)重置门 Γ u \Gamma_{u} Γu?: 控制候选状态 c ~ ( t ) \tilde{\boldsymbol{c}}^{(t)} c~(t)的计算是否依赖上一时刻 c < t ? 1 > c^{<t-1>} c<t?1>
- 生成候选状态
c ~ ( t ) = tanh ? ( ω c [ Γ r c ? t ? 1 ? , x ( t ) ] + b c ) \tilde {c}^{(t)}=\tanh \left(\omega_{c}\left[{\Gamma_r }c^{\langle t-1\rangle}, x^{(t)}\right]+b_{c}\right) c~(t)=tanh(ωc?[Γr?c?t?1?,x(t)]+bc?)
- 候选值即记忆细胞的候选值,存储的是新的信息,当 Γ u \Gamma_{u} Γu?等于1时,即完全抛弃旧值时, c ? t ? = c ~ ( t ) c^{\langle t\rangle} =\tilde{c}^{(t)} c?t?=c~(t),不严格的说,存储的就是当前层的激活值.
- Γ r {\Gamma_r } Γr?表示是否候选值是否依赖于上一时刻的值
c ? t ? = Γ u ? c ^ ( t ) + ( 1 ? Γ u ) ? c ? t ? 1 ) c^{\langle t\rangle}=\Gamma_{u} * \hat{c}^{(t)}+\left(1-\Gamma_{u}\right) * c^{\langle t-1)} c?t?=Γu??c^(t)+(1?Γu?)?c?t?1)
u u u表示update
Γ u \Gamma_{u} Γu?等于0时, 等于 c ? t ? 1 ) c^{\langle t-1)} c?t?1),即不要更新值,使用旧值
Γ u \Gamma_{u} Γu?等于1时,等于$ \tilde{c}^{(t)}$
作为一个门,如果这个门不开,即为0,那么说明记忆细胞还要存储之前存的信息,如果这门要开一点,那么就要"挤进"一点当前层的信息,"赶走"一点原来的信息,如果这个门完全打开,就用当前层的信息覆盖记忆细胞的信息
c ? t ? = a ? t ? c^{\langle t\rangle}=a^{\langle t\rangle} c?t?=a?t?
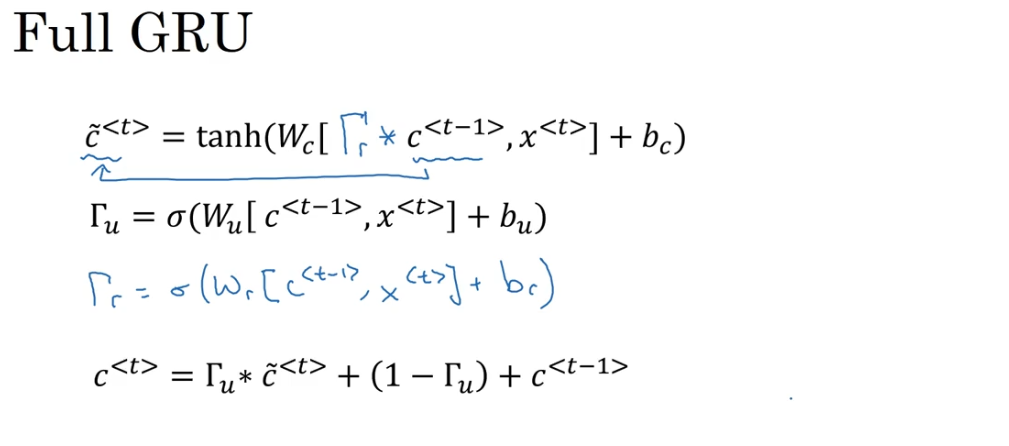
改进版
Γ r \Gamma_{r} Γr?其中 r r r表示相关性
长短时记忆网络LSTM (Long Short Term Memory )
传统RNN中的存储着历史信息 a t a_t at?,但是 a t a_t at?每个时刻都会被重写,因此可以看做一种短期记忆。长期记忆可以看做是网络内部的某些参数,隐含了从数据中学到的经验,其更新周期要远远比短期记忆慢。
比GRU更强大和通用
基本原理
为保持一致性,均使用吴恩达深度学习课程中的符号
h t ? 1 = a t ? 1 , Γ f = f t , Γ u = f i , Γ o = f t h_{t-1} =a_{t-1},\Gamma_{f} = f_t ,\Gamma_{u} = f_i,\Gamma_{o} = f_t ht?1?=at?1?,Γf?=ft?,Γu?=fi?,Γo?=ft?

- LSTM引入三个门来控制信息传递
(1) 遗忘门 Γ f \Gamma_{f} Γf? 控制上一时刻的内部状态 c t ? 1 c_{t-1} ct?1?,需要遗忘多少信息
(2) 输入门 Γ u \Gamma_{u} Γu? 控制当前时刻的候选状态 c ~ t \tilde{\boldsymbol{c}}_{t} c~t?,需要保留多少信息
(2) 输入门 Γ o \Gamma_{o} Γo? 控制当前时刻的内部状态 c t \boldsymbol{c}_{t} ct?,需要输出多少信息到外部状态 a t a_t at?
- 计算
Γ
u
=
σ
(
W
u
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
u
)
\Gamma_{u}=\sigma\left(W_{u}\left[a^{<t-1>}, x^{<t>}\right]+b_{u}\right)
Γu?=σ(Wu?[a<t?1>,x<t>]+bu?)
Γ
f
=
σ
(
W
f
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
f
)
\Gamma_{f}=\sigma\left(W_{f}\left[a^{<t-1>}, x^{<t>}\right]+b_{f}\right)
Γf?=σ(Wf?[a<t?1>,x<t>]+bf?)
Γ
o
=
σ
(
W
o
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
o
)
\left.\Gamma_{o}=\sigma(W_{o}\left[a^{<t-1>}, x^{<t>}\right]+b_{o}\right)
Γo?=σ(Wo?[a<t?1>,x<t>]+bo?)
c ~ < t > = tanh ? ( W c [ a < t ? 1 > , x < t > ] + b c ) \tilde{c}^{<t}>=\tanh \left(W_{c}\left[a^{<t-1>}, x^{<t>}\right]+b_{c}\right) c~<t>=tanh(Wc?[a<t?1>,x<t>]+bc?)
c
<
t
>
=
Γ
u
?
c
~
<
t
>
+
Γ
f
?
c
<
t
?
1
>
?
\left.c^{<t>}=\Gamma_{u} * \tilde{c}^{<t>}+\Gamma_{f} * c^{<t-1>}\right\rangle
c<t>=Γu??c~<t>+Γf??c<t?1>?
a
<
t
>
=
Γ
o
?
tanh
?
c
<
t
>
a^{<t>}=\Gamma_{o} * \tanh c^{<t>}
a<t>=Γo??tanhc<t>
(1) 先利用上一时刻外部状态 a t ? 1 a_{t-1} at?1?和当前时刻的输入,计算三个门和候选状态 c ~ < t > \tilde{c}^{<t>} c~<t>的值
(2) 结合遗忘门和输入门来更新内部状态(记忆单元) c t c_t ct?
(3) 结合输出门控制内部状态的信息传递到外部状态 h t h_t ht?
问题: 点乘,叉乘

GRU和LSTM对比
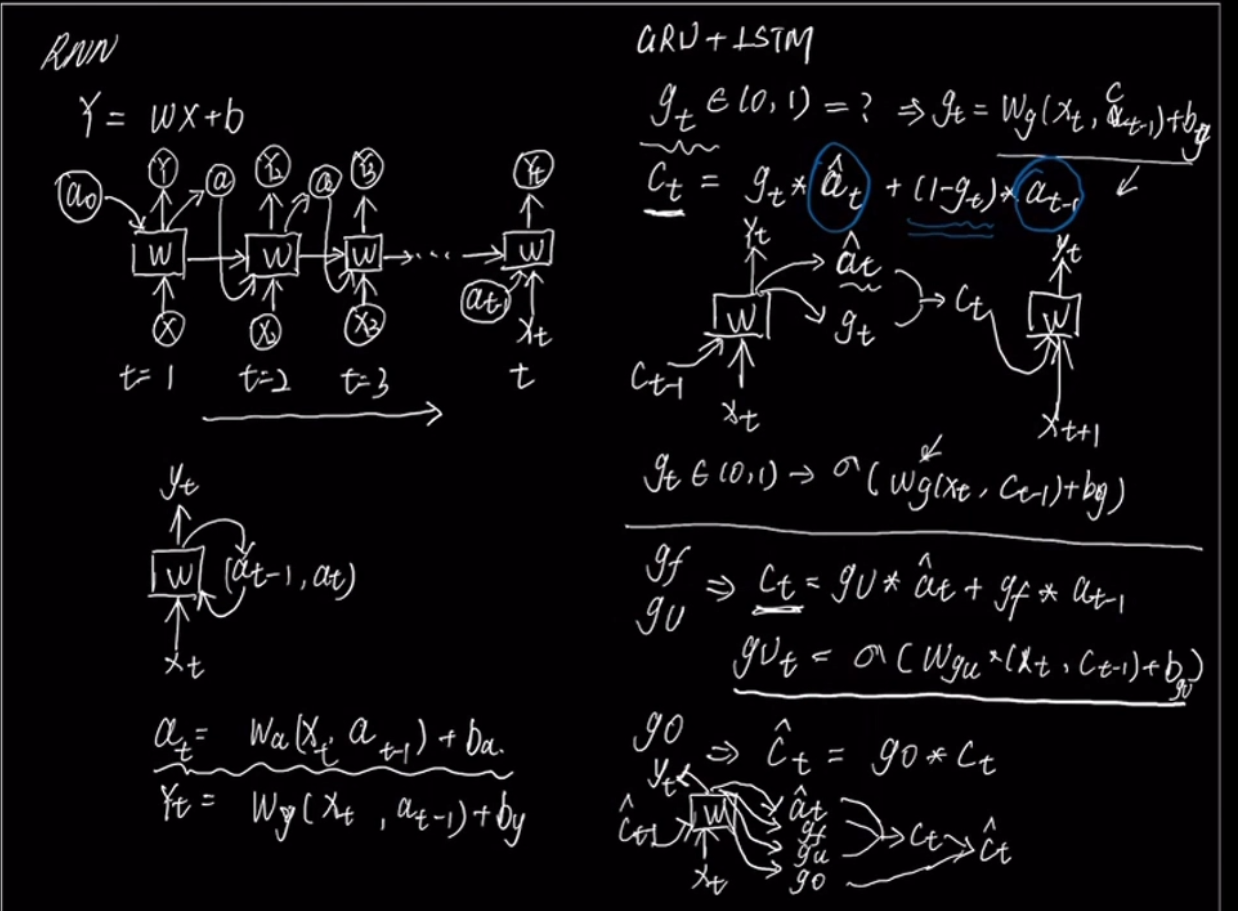
GRU在对于当前的信息和过去的信息面临着二选一的状况,选了90%的现在的信息,那么过去的信息大多就要被舍弃,只通过加入一个门 g t g_t gt?来实现
LSTM这点上是做的更全面,通过三个门 g u , g f , g o g_u,g_f,g_o gu?,gf?,go?来实现,以独立的门来控制当前层的信息需要多少,记忆细胞中原来的信息保留多少
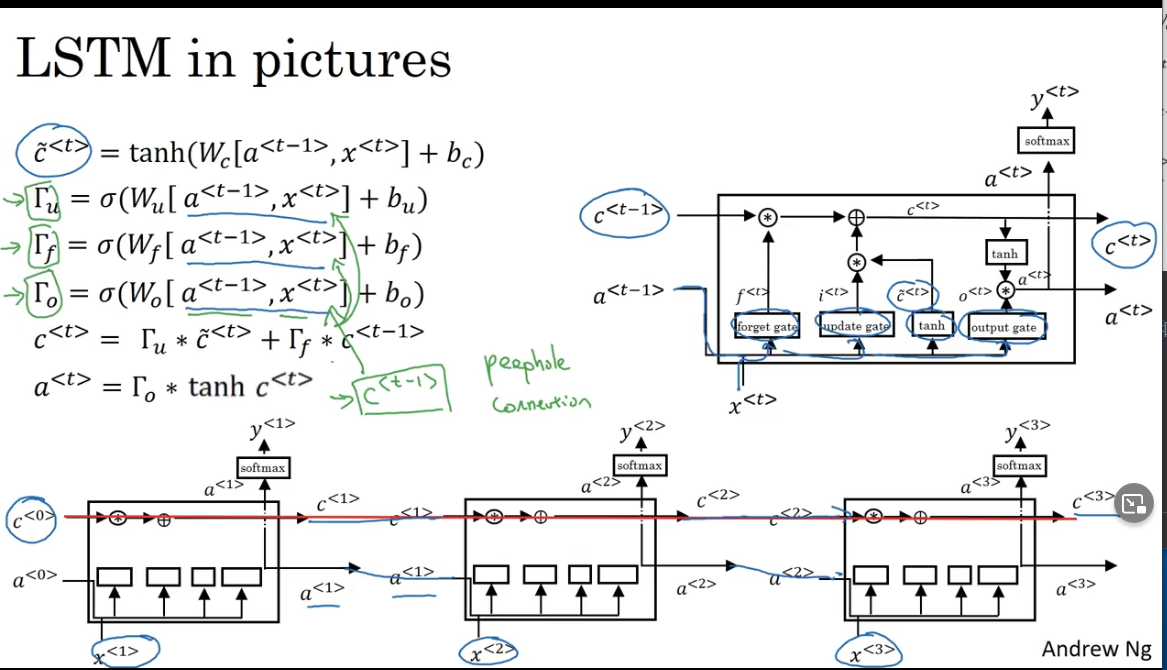
c < t > c^{<t>} c<t>是记忆单元,是LSTM的核心部分,可以在某个状态捕捉到关键信息,并有能力将此关键信息保存一定的时间间隔
如何保存关键信息可以通过遗忘门 Γ f \Gamma_{f} Γf?和输入门 Γ u \Gamma_{u} Γu?控制,因此内部状态 c < t > c^{<t>} c<t>保存信息的周期要长于短期记忆,但又短于长期记忆,(或者说,关键信息中既有长期记忆的部分,也有短期记忆的部分),因此成为长短期记忆
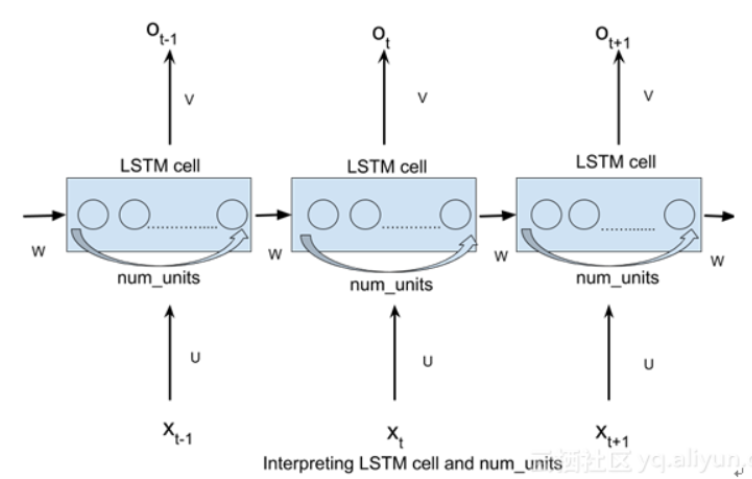

代码来看LSTM
LSTM的输入
- batch_size
- time_step
- input_embedding_size : 输入词向量维度
- num_units: 隐层神经元个数
对于每个时间步:
Γ
u
=
σ
(
W
u
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
u
)
\Gamma_{u}=\sigma\left(W_{u}\left[a^{<t-1>}, x^{<t>}\right]+b_{u}\right)
Γu?=σ(Wu?[a<t?1>,x<t>]+bu?)
Γ
f
=
σ
(
W
f
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
f
)
\Gamma_{f}=\sigma\left(W_{f}\left[a^{<t-1>}, x^{<t>}\right]+b_{f}\right)
Γf?=σ(Wf?[a<t?1>,x<t>]+bf?)
Γ
o
=
σ
(
W
o
[
a
<
t
?
1
>
,
x
<
t
>
]
+
b
o
)
\left.\Gamma_{o}=\sigma(W_{o}\left[a^{<t-1>}, x^{<t>}\right]+b_{o}\right)
Γo?=σ(Wo?[a<t?1>,x<t>]+bo?)
c ~ < t > = tanh ? ( W c [ a < t ? 1 > , x < t > ] + b c ) \tilde{c}^{<t}>=\tanh \left(W_{c}\left[a^{<t-1>}, x^{<t>}\right]+b_{c}\right) c~<t>=tanh(Wc?[a<t?1>,x<t>]+bc?)
c
<
t
>
=
Γ
u
?
c
~
<
t
>
+
Γ
f
?
c
<
t
?
1
>
?
\left.c^{<t>}=\Gamma_{u} * \tilde{c}^{<t>}+\Gamma_{f} * c^{<t-1>}\right\rangle
c<t>=Γu??c~<t>+Γf??c<t?1>?
a
<
t
>
=
Γ
o
?
tanh
?
c
<
t
>
a^{<t>}=\Gamma_{o} * \tanh c^{<t>}
a<t>=Γo??tanhc<t>
输入数据维度为 [batch_size*input-embedding_size]
矩阵 W x W_x Wx?维度为[input-embedding_size*num_untis]
隐层输出数据:[batch_size*num_units]
矩阵 W h W_h Wh?的维度为[num_units*num_units]
上一时刻的输出 h t ? 1 h_{t-1} ht?1?数据维度为**[num_units](实际上是[batch_size*num_units]**)
每个时间步都是这样的,所以隐层在所有时间步(堆叠)乘上权重后,形成的Tensor为
[time_step,batch_size,num_units]或者[batch_size,time_step,num_units]
LSTM内部网络

门gate即实际上就是一层全连接层,它的输入是一个向量,输出是一个0到1之间的实数向量
可以看到中间的cell 里面有四个黄色小框,每一个小黄框代表一个前馈网络层,num_units(即HIDDEN_SIZE, 隐藏层结点个数)就是这个层的隐藏神经元个数,其中1、2、4的激活函数是sigmoid,3的激活函数是tanh
cell的权重是共享的,这是什么意思呢?这是指这张图片上有三个绿色的大框,代表三个 cell对吧,但是实际上,它只是代表了一个 cell在不同时序时候的状态,所有的数据只会通过一个cell然后不断更新它的权重。
nn.LSTM()参数解析
参数
– input_size
– hidden_size
– num_layers
– bias
– batch_first
– dropout
– bidirectional
输入
input,( h 0 , c 0 h_0,c_0 h0?,c0?),其中,如果 h 0 , c 0 h_0,c_0 h0?,c0?未提供,那么以0矩阵为初始化矩阵
-
input (seq_len, batch, input_size)
-
h_0 (num_layers * num_directions, batch, hidden_size)
t=0时候没有上一时刻信息可用,所以通过随机初始化方式,定义 h 0 , c 0 h_0,c_0 h0?,c0?
h 0 h_0 h0?表示上一时刻的输出,是短期记忆信息
-
c_0 (num_layers * num_directions, batch, hidden_size)
h 0 h_0 h0?表示之前的记忆信息,是长期记忆信息
输出
-
output (seq_len, batch, num_directions * hidden_size)
-
h_n (num_layers * num_directions, batch, hidden_size)
-
c_n (num_layers * num_directions, batch, hidden_size)
参数详解
-
input_size:
输入x的向量里有多少个元素 输入的x一般为一个字的embedding 或者说 就是embedding size
-
hidden_size: The number of features in the hidden state
h -
num_layers: Number of recurrent layers. E.g., setting
num_layers=2would mean stacking two LSTMs together to form astacked LSTMwith the second LSTM taking in outputs of the first LSTM and computing the final results. Default: 1LSTM 堆叠的层数,默认值是1层,如果设置为2,第二个LSTM接收第一个LSTM的计算结果。
相当于多个Lstm串联
-
batch_first: If
True, then the input and output tensors are provided as(batch, seq, feature)instead of(seq, batch, feature).Note that this does not apply to hidden or cell states. See the Inputs/Outputs sections below for details. Default:False判断输入输出的第一维是否为 batch_size,默认值 False。故此参数设置可以将 batch_size 放在第一维度。
torch.LSTM 中 batch_size 维度默认是放在第二维度,故此参数设置可以将 batch_size 放在第一维度。
-
dropout: If non-zero, introduces a
Dropoutlayer on the outputs of each LSTM layer except the last layer, with dropout probability equal to :attr:dropout. Default: 0
默认值0。是否在除最后一个 RNN 层外的其他 RNN 层后面加 dropout 层。输入值是 0-1 之间的小数,表示概率。0表示0概率dripout,即不dropout
- bidirectional – If True, becomes a bidirectional LSTM. Default: False
num_layers: Number of recurrent layers. E.g., setting ``num_layers=2``
would mean stacking two LSTMs together to form a `stacked LSTM`,
with the second LSTM taking in outputs of the first LSTM and
computing the final results. Default: 1
bias: If ``False``, then the layer does not use bias weights `b_ih` and `b_hh`.
Default: ``True``
bidirectional: If ``True``, becomes a bidirectional LSTM. Default: ``False``
proj_size: If ``> 0``, will use LSTM with projections of corresponding size. Default: 0
双向LSTM
单向LSTM仅保留过去的信息,因为它只能看到过去的信息.
使用双向将以两种方式运行您的输入,一种从过去到将来,另一种从将来到过去,这种方法与单向的不同之处在于,在向后运行的LSTM中,您保留了未来的信息并结合使用两个隐藏状态,您可以在任何时间点保存过去和将来的信息.
双向卷积神经网络的隐藏层要保存两个值, A 参与正向计算, A’ 参与反向计算。
最终的输出值 y 取决于 A 和 A’:
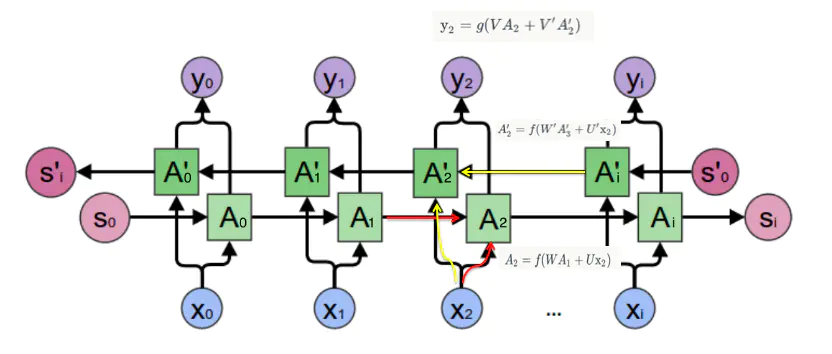
即正向计算时,隐藏层的 s_t 与 s_t-1 有关;反向计算时,隐藏层的 s_t 与 s_t+1 有关
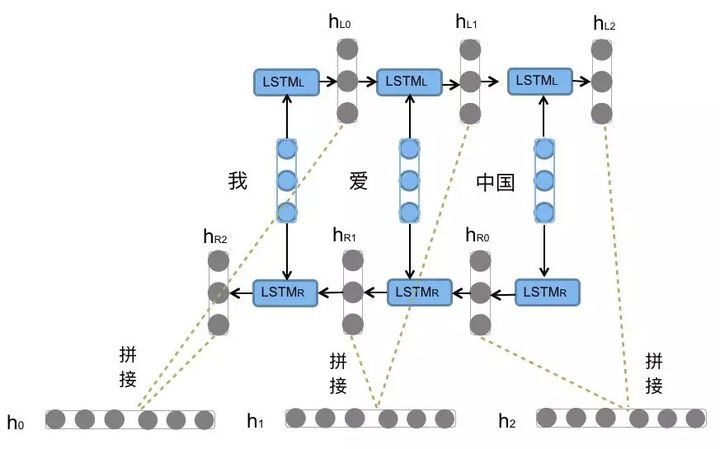
举例说明
前向的LSTM与后向的LSTM结合成BiLSTM。比如,我们对“我爱中国”这句话进行编码,模型如图6所示