一、混合灰狼优化布谷鸟搜索优化算法
1 基本灰狼优化算法
作为一种仿生群体智能优化算法, 灰狼优化算法通过模仿自然界灰狼群体的社会领导层级机制和捕食行为提出。与其他元启发式算法类似, 该算法首先随机产生一组候选解, 每次迭代选出最好的三个候选解称为alpha、beta和delta, 由它们带领整个种群朝着最优解方向移动。种群中的其他个体omega追随alpha、beta和delta搜寻更好的解。灰狼种群的包围捕食行为可以通过下述数学式进行描述。
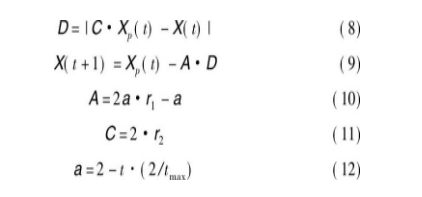
其中:t为当前迭代次数;tmax为种群的最大迭代次数;A和C是协同系数向量;Xp表示猎物的位置向量;X表示灰狼的位置向量;a随着迭代过程从2~0线性递减;r1和r2是[0, 1]中的随机数向量。为了找到问题的最优解, 每个omega灰狼个体的位置更新式如下:
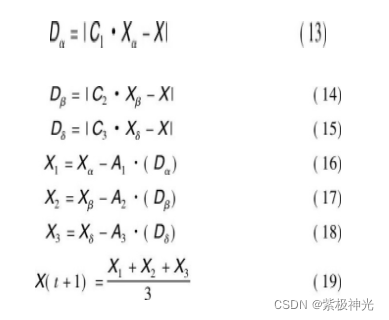
另外, Mirjalili等人[2]指出在上述公式中参数A和C决定灰狼优化算法的全局搜索和局部搜索, 当|A|>1时算法进行全局搜索, 当|A|<1时进行局部搜索。参数C的随机产生可以有效避免算法陷入局部最优。虽然上述操作可以在一定程度上提高收敛效率和避免早熟收敛, 但是由于灰狼优化算法的种群寻优过程本质上是由最优的三个候选解alpha、beta和delta主导, 该算法往往倾向于早熟收敛, 陷入局部最优值不再跳出。因此, 如果在该算法中对最优候选解进行一定的变异操作, 能够有效帮助算法找到更好的解。
2 改进混合灰狼优化算法
2.1 进化种群动态操作
Saremi等人[3]在GWO算法中引入进化种群动态操作 (EPD) , 就是将种群中差的个体移除, 已有研究证明EPD能够改善整个种群适应度的中值, 是一种改进元启发式算法性能的简单有效方法。在混合灰狼优化算法的每一次迭代中, 通过EPD操作将种群中差的一半个体位置清除, 然后在四个位置以相等概率重新随机生成它们的新位置。这四个位置分别是位于alpha、beta和delta周围 (改善整个种群中值) , 以及搜索空间的随机位置 (避免陷入局部最优) 。由于Saremi等人提出的混合灰狼优化算法是针对连续函数优化问题设计, 不能直接用于求解离散的组合优化问题。所以, 本文对该操作进行改进, 改进后的四个位置更新式如下:
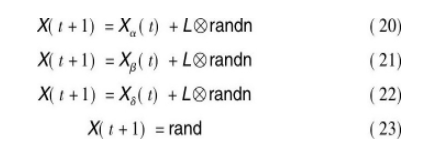
其中, Xα (t) 、Xβ (t) 和Xδ (t) 分别表示alpha、beta和delta个体的当前位置;rand是[0, 1]中的随机数向量;randn是服从标准正态分布的随机数向量, 可以是正或负值;代表矢量运算;L表示步长向量。此处引入布谷鸟搜索算法中的Lévy飞行方式[11], 可以有效防止GWO算法早熟收敛, 其计算公式为

其中:β是一个[1, 2]的参数, 此处取β=1.5[11,16];u和v服从正态分布。
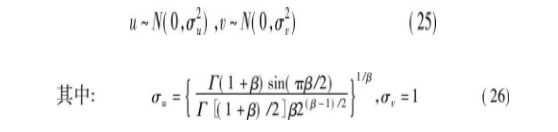
2.2 反向学习初始化种群
对基于种群迭代的群体智能优化算法来说, 初始种群的好坏直接影响着算法的全局搜索效率和解的质量, 多样性较好的初始种群对提高算法的寻优性能有很大帮助。然而, 标准GWO算法在迭代开始前通过随机初始化产生种群个体, 难以确保初始群体的多样性, 从而在一定程度上影响了算法的搜索效率。本文将采用反向学习策略来产生初始种群。Tizhoosh在2005年提出了反向学习策略, 目前已在GA、DE、ACO等群体智能优化算法中得到了成功的应用。采用反向学习策略产生初始种群个体的具体操作步骤如下:
a) 在搜索空间中随机初始化N个灰狼个体的位置xi, j (i=1, 2, …, D;j=1, 2, …, N) 作为初始种群P1。在作业车间调度问题的编码中xi, j∈[0, 1]中的随机数, D为每个灰狼个体的维数, 即工序总数;N为种群个数。
b) 生成初始种群P1中每个灰狼个体xi, j的反向个体xi, j'构成反向种群P2, xi, j'=1-xi, j。
c) 合并种群P1和P2, 将2N个灰狼个体按照适应度值进行升序排序, 选取适应度值前N个灰狼个体作为最终的初始种群。
2.3 变异算子
由于基于精英保存策略, 在GWO算法进化后期, 群体中所有灰狼个体均向最优个体区域靠近, 从而导致种群丧失多样性, 如果此时当前最优灰狼个体alpha为局部最优解, 则GWO算法将陷入局部最优, 出现早熟收敛现象, 这也是很多群体智能优化算法的弊端。为了降低GWO算法出现早熟现象和陷入局部最优值的概率, 本文对群体中当前最优灰狼个体alpha进行多样性变异操作, 其原理是:对最优个体alpha中的每一维元素以1/D的概率进行变异。变异操作公式为

其中:ε是一个很小的正数, 经过测试此处ε=0.01算法优化效果最好;rand是[0, 1]中的随机数向量;K是一个0和1组成的向量, 各维元素Kj的取值公式如下所示, rj是[0, 1]的一个随机数, 当rj≤1/D, Kj=1, 否则Kj=0。

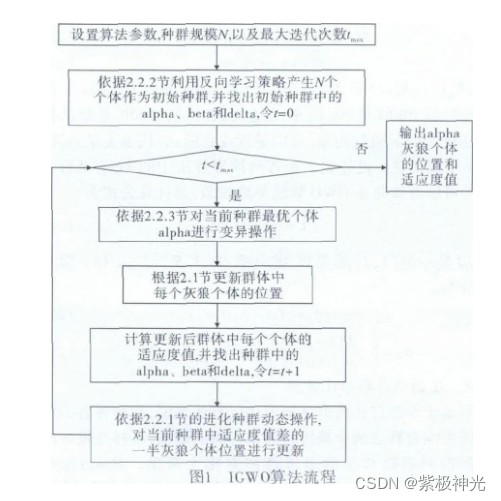
通过对标准GWO算法进行进化种群动态、反向学习初始化种群, 以及最优个体变异三方面的改进操作, 改进后的混合灰狼优化算法拥有更佳的寻优性能, 同时跳出局部最优解的能力更强。本文将改进后的混合灰狼优化算法简称为IGWO, 运用所提出的IGWO算法求解作业车间调度问题的算法流程如图1所示。
二、部分代码
clear all
clc
close all
warning off
SearchAgents_no=20; % 搜索代理数量
Function_name='F1'; % 测试功能的名称,可以从 F1 到 F23
Max_iteration=200; % 最大迭代次数
Run_no = 20;
for k = 1 : 1 : Run_no
% 加载所选基准函数的详细信息
[lb,ub,dim,fobj]=Get_Function_details(Function_name);
[Best_score_CS2,Best_pos_CS2,AGWOCS_cg_curve]=AGWO_CS(SearchAgents_no,Max_iteration,lb,ub,dim,fobj); % Augmented GWO- Cuckoo Search.
BestSolutions1(k) = Best_score_CS2;
Average= mean(BestSolutions1);
Mean=mean(BestSolutions1);
StandDP=std(BestSolutions1);
Med = median(BestSolutions1);
[BestValueP I] = min(BestSolutions1);
[WorstValueP IM] = max(BestSolutions1);
disp(['Run # ' , num2str(k), ' Best_score_AGWOCS : ' , num2str( Best_score_CS2)]);
end
disp([ 'Best=',num2str( BestValueP)]);
disp([ 'Worst=',num2str(WorstValueP)]);
disp([ 'Average=',num2str( Average)]);
disp([ 'Mean=',num2str( Mean)]);
disp([ 'Standard Deviation=',num2str( StandDP)]);
disp([ 'Median=',num2str(Med)]);
figure('Position',[300 190 980 490])
%figure('Position',[300 190 500 270])
%绘制搜索空间
subplot(1,2,1);
func_plot(Function_name);
title('目标坐标')
xlabel('x_1');
ylabel('x_2');
zlabel([Function_name,'( x_1 , x_2 )'])
%颜色图
%绘制目标坐标
subplot(1,2,2);
%semilogy(GWO_cg_curve,'Color','r')
hold on
semilogy(AGWOCS_cg_curve,'Color','m')
title('目标坐标')
xlabel('I迭代');
ylabel('最优值');
axis tight
grid on
box on
%legend('AGWO-CS')
legend({'AGWO-CS'},'FontSize',2,'location','best')
三、运行结果

四、matlab版本及参考文献
1 matlab版本
2014a
2 参考文献
[1] 包子阳,余继周,杨杉.智能优化算法及其MATLAB实例(第2版)[M].电子工业出版社,2016.
[2]张岩,吴水根.MATLAB优化算法源代码[M].清华大学出版社,2017.
[3]姚远远,叶春明.求解作业车间调度问题的改进混合灰狼优化算法[J].计算机应用研究. 2018,35(05)