深度学习中的数学-概率论
1 随机变量
一个随机变量只是对可能的状态的描述;它必须伴随着一个概率分布来指定每个状态的可能性
随机变量可以是离散的或者连续的。离散随机变量拥有有限或者可数无限多的状态。注意这些状态不一定非要是整数;它们也可能只是一些被命名的状态而没有数值。连续随机变量伴随着实数值
2 概率分布
概率分布(probability distribution) 用来描述随机变量或一簇随机变量在每一个可能取到的状态的可能性大小。我们描述概率分布的方式取决于随机变量是离散
的还是连续的。
2.1 离散变量
离散型变量的概率分布可以用 概率质量函数( probability mass function, PMF) 来描述,用来表示随机变量能够取得状态的概率。x = x x x 的概率用 P( x x x) 来表示,为了表示方便可以写为P(x = x x x)。x ~ P(x) 表示随机变量 x 遵循的分布
概率质量函数可以同时作用于多个随机变量。这种多个变量的概率分布被称为 联合概率分布( joint probability distribution)。 P(x = x x x; y = y y y) 表示 x = x x x 和 y = y y y 同时发生的概率。我们也可以简写为 P( x , y x,y x,y)
2.2 连续变量
当研究的对象是连续型随机变量时,我们用 概率密度函数( probability density function, PDF)
如果一个函数 p 是概率密度函数,必须满足下面这几个条件:
? p 的定义域必须是 x 所有可能状态的集合
? 任意
x
x
x ∈ x, p(
x
x
x) ≥ 0: 注意,我们并不要求 p(
x
x
x) ≤ 1
? ∫ p(
x
x
x)d
x
x
x = 1
概率密度函数 p(x) 并没有直接对特定的状态给出概率,相对的,它给出了落在面积为 δx 的无限小的区域内的概率为 p(x)δx
在单变量的例子中, x x x 落在区间 [a; b] 的概率是 ∫ [ a ; b ] p ( x ) d x ∫_{[a;b]} p(x)dx ∫[a;b]?p(x)dx
3 边缘概率
有时候,我们知道了一组变量的联合概率分布,但想要了解其中一个子集的概率分布。这种定义在子集上的概率分布被称为 边缘概率分布( marginal probability distribution)。
例如,假设有离散型随机变量 x 和 y,并且我们知道 P(x; y)。我们可以依据下面的 求和法则( sum rule) 来计算 P(x):

‘‘边缘概率’’ 的名称来源于手算边缘概率的计算过程。当 P(x; y) 的每个值被写在由每行表示不同的 x 值,每列表示不同的 y 值形成的网格中时,对网格中的每行
求和是很自然的事情,然后将求和的结果 P(x) 写在每行右边的纸的边缘处
| - | y 1 y_1 y1? | y 1 y_1 y1? | y 1 y_1 y1? | sum(边缘概率) |
|---|---|---|---|---|
| x 1 x_1 x1? | 0.1 | 0.1 | 0.1 | 0.3 |
| x 2 x_2 x2? | 0.1 | 0.1 | 0.1 | 0.3 |
| x 3 x_3 x3? | 0.1 | 0.1 | 0.2 | 0.4 |
对于连续型变量,我们需要用积分替代求和:

4 条件概率
4.1 计算公式
将给定 x =
x
x
x, y =
y
y
y 发生的条件概率记为P(y =
y
y
y | x =
x
x
x)。这个条件概率可以通过下面的公式计算:

条件概率只在 P(x =
x
x
x) > 0 时有定义。我们不能计算给定在永远不会发生的事件上的条件概率
4.2 条件概率的链式法则
任何多维随机变量的联合概率分布,都可以分解成只有一个变量的条件概率相乘的形式(称为概率的链式法则chain rule)

例如求三个变量的联合概率(使用两次条件概率公式):

5 独立性和条件独立性
两个随机变量的联合概率分布可以表示成乘积的形式,称这两个变量是相互独立的:
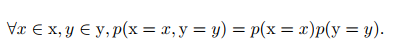
如果关于 x 和 y 的条件概率分布对于 z 的每一个值都可以写成乘积的形式,那么这两个随机变量 x 和 y 在给定随机变量 z 时是 条件独立的
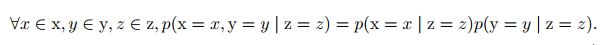
符号表示:x⊥y 表示 x 和 y 相互独立, x⊥y | z 表示 x 和 y 在给定 z 时条件独立
6 期望、方差和协方差
函数 f(x) 关于某分布 P(x) 的 期望( expectation) 或者 期望值( expected value) 是指,当 x 由 P 产生, f 作用于 x 时, f(x) 的平均值
对于离散随机变量可以求和得到:
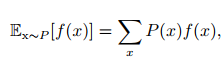
对于连续型随机变量可以积分得到:
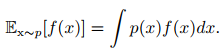
期望是线性的,如:
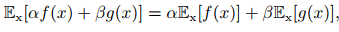
方差( variance) 衡量的是当我们对 x 依据它的概率分布进行采样时, 随机变量 x 的函数值会呈现多大的差异:
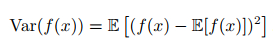
当方差很小时, f(x) 的值形成的簇比较接近它们的期望值。 方差的平方根被称为 标准差( standard deviation)
协方差( covariance)在某种意义上给出了两个变量线性相关性的强度以及这些变量的尺度:
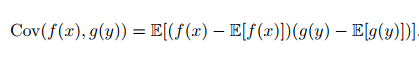
协方差的绝对值如果很大则意味着变量值变化很大并且它们同时距离各自的均值很远。如果协方差是正的,那么两个变量都倾向于同时取得相对较大的值。如果协方差是负的,那么其中一个变量倾向于取得相对较大的值的同时,另一个变量倾向于取得相对较小的值,反之亦然。其他的衡量指标如 相关系数( correlation) 将每个变量的贡献归一化,为了只衡量变量的相关性而不受各个变量尺度大小的影响
随机向量
x
∈
R
n
x ∈ R^n
x∈Rn 的 协方差矩阵( covariance matrix)是一个 n × n 的矩阵,并且满足
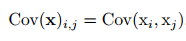
协方差矩阵的对角元是方差:
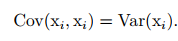
7 常用概率分布
待补充
7.1 高斯分布

当我们由于缺乏关于某个实数上分布的先验知识而不知道该选择怎样的形式时, 正态分布是默认的比较好的选择,其中有两个原因
第一,我们想要建模的很多分布的真实情况是比较接近正态分布的。 中心极限定理( central limit theorem)说明很多独立随机变量的和近似服从正态分布。这意味着在实际中,很多复杂系统都可以被成功地建模成正态分布的噪声,即使系统可以被分解成一些更结构化的部分
第二,在具有相同方差的所有可能的概率分布中, 正态分布在实数上具有最大的不确定性。因此,我们可以认为正态分布是对模型加入的先验知识量最少的分布
正态分布可以推广到
R
n
R^n
Rn 空间,这种情况下被称为 多维正态分布( multivariatenormal distribution)。它的参数是一个正定对称矩阵 Σ:
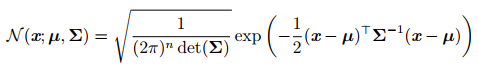
参数 μ 仍然表示分布的均值,只不过现在是向量值。参数 Σ 给出了分布的协方差矩阵