[人工智能]【知识建设】信息熵、条件熵、互信息、交叉熵及相对熵（KL散度）

一、信息熵

1. 定义

衡量一个随机变量$X$的信息量，用$H$表示

根据这个定义，这应该是个不确定的值（随机变量是变化的），而数学上使用期望来将这种不确定性量化：

$H={\sum }_{x\in X}P(x)?x$的信息量

其中$x$为随机变量$X$的不同取值

那么问题就变成了如何在具体的情形（即一个事件）下，估算随机变量的信息量

2. 语义理解

先从语义上理解信息量应该满足的条件，当一件事的不确定性越大（概率越小），那么它所包含的信息量就应该越大，相反，不确定性越小（概率越大），包含的信息量就越小；比如太阳从东边升起这件事是非常确定的，不确定性很小，那么你告诉我也不会改变什么，也就是没什么信息量。由此得知，信息量应该是关于概率的连续函数，其大小应该跟概率成反比，概率的范围是$[0,1]$，那么信息量就应该是以$[0,1]$为定义域的连续函数

另外，信息量还应该保证不是负值（一件事揭露的信息量应该至少为0，不可能是负值）（也就是说信息量在定义域$[0,1]$上应为非负值）；具有可加性（同时告知两件事，应该比告知一件事的信息量大或相等）（其实可加性就指示了应该使用$log$函数了）；概率越小，信息量的增加速度越快，反之，信息量增加速度越慢，也就是说在定义域$[0,1]$上斜率应该递减（仍然参考太阳的例子）

3. 公式

那么满足上诉四个条件的函数，也就是负对数函数（或许还有别的吧，但是负对数函数非常常用），公式为$?log(x)$。而具体事件$x$的信息量，在信息论中也称为自信息。综上所述，信息熵的整体公式应为：

$H=?{\sum }_{x\in X}P(x)?logP(x)$

4. 自信息与信息熵

自信息表示一个确定事件的信息量，即一个事件的不确定性；而信息熵表示随机变量或整个系统的不确定性，是随机变量在不同事件下的信息量的期望，所以信息熵越大，表示该系统的不确定性越大

二、条件熵

$H(Y|X)$，定义为$X$给定条件下$Y$的条件分布的熵对$X$的数学期望

这个定义也太拧巴了，可以理解为，在已知$X$事件的情况下，事件$Y$的信息量。而$X$是一个不确定事件，因此需要通过将$X$化为具体事件$x$，分别计算不同$x$下Y的信息量，则公式应为：

$H(Y|X)={\sum }_{x\in X}P(x)H(Y|X=x)$

那么就要计算$H(Y|X=x)$，即，在确定事件$x$下，计算$Y$的信息量，同样的，需要化为$Y$的具体事件：

$H(Y|X)=?{\sum }_{x\in X}P(x){\sum }_{y\in Y}P(y|x)logP(y|x)$

根据条件概率的转化公式：

$H(Y|X)=?{\sum }_{x\in X}{\sum }_{y\in Y}P(x,y)logP(y|x)$

三、互信息

1. 定义

衡量随机变量之间相互依赖程度的度量

2. 公式

假如有两个随机变量$X$，$Y$，那么要衡量$Y$变量对$X$变量的影响，就应该去计算，在未知$Y$变量的情况下$X$变量的信息量，和已知$Y$变量的情况下$X$变量的信息量，即：

$I(X;Y)=H(X)?H(X|Y)$

结合上面对于信息熵和条件熵的解释，我们对齐进行整理：

$I(X;Y)=?{\sum }_{x\in X}P(x)?logP(x)+{\sum }_{x\in X}{\sum }_{y\in Y}P(x,y)logP(x|y)$

其中根据全概率公式$P(x)={\sum }_{y\in Y}P(x,y)$，得到：

$I(X;Y)=?{\sum }_{x\in X}{\sum }_{y\in Y}P(x,y)?logP(x)+{\sum }_{x\in X}{\sum }_{y\in Y}P(x,y)logP(x|y)$

然后可以合并同类项$P(x,y)$：

$I(X;Y)={\sum }_{x\in X}{\sum }_{y\in Y}P(x,y)?log\frac{P(x,y)}{P(x)P(y)}$

3. 应用

互信息和信息熵的关系可以通过下图表示：

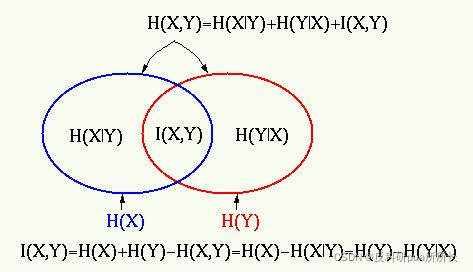
经常见到的目标是，要使互信息最大化，就是最大化两个随机事件的相关性，在深度学习中，就是最大化数据集所拟合出的分布的相关性

当两个随机变量相同时，互信息最大，公式：

$I(X;X)=H(X)?H(X|X)=H(X)$

四、交叉熵

这里先引入对信息熵的另一种理解，即为了消除某随机变量的不确定性要付出的最小努力。当你正确估计随机变量的分布（即真实分布，记为$p(x)$）时，这种努力会达到最小；相反，当你得到的是非真实分布（记为$q(x)$）时，就要为了消除随机变量的不确定性付出更多努力。而我们要衡量这种非真实分布下要付出的努力，就用到了交叉熵：

$H(p,q)=?{\sum }_{x\in X}p(x)logq(x)$

$p(x)$为随机变量的特定取值下的概率，这个是不变的，而$logq(x)$表示随机变量特定取值下，为了消除不确定性所付出的努力，这一点是与对分布的估计相关的，当你正确估计，则付出的努力小，反之，付出的努力大；

而许多地方消除了负号，写作下面的形式：

$H(p,q)={\sum }_{x\in X}p(x)log\frac{1}{q(x)}$

五、相对熵，也称为KL散度

上一部分我们谈到，信息熵可以理解为，为了消除不确定性所付出的最小努力，而交叉熵衡量了错误估计随机变量的分布时，消除不确定性所付出的努力；那么如何去衡量这种错误估计时的努力，与需要付出的最小努力，他们之间的差异呢？就用到了相对熵。

根据这种理解，我们可以结合信息熵和交叉熵的公式（仍然假设$p$为真实分布）：

$D_{KL}(p||q)=H(p,q)?H(p)$

代入，

$D_{KL}(p||q)=?{\sum }_{x\in X}p(x)logq(x)+{\sum }_{x\in X}p(x)logp(x)$

稍作整理，

$D_{KL}(p||q)={\sum }_{x\in X}p(x)log\frac{p(x)}{q(x)}$

六、结束语

两天了，终于整理完confuse我两年的小登西。谢谢下面参考：

信息熵是什么？ - 运筹之学的回答 - 知乎

通俗理解条件熵 - 忆臻的文章 - 知乎

什么是「互信息」？ - 甜草莓的回答 - 知乎

如何通俗的解释交叉熵与相对熵？ - Peiwen的回答 - 知乎

详解机器学习中的熵、条件熵、相对熵和交叉熵