[人工智能] 视觉里程计 -- 单层多层直接法（附代码解析）

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 视觉里程计 -- 单层多层直接法（附代码解析） -> 正文阅读

[人工智能]视觉里程计 -- 单层多层直接法（附代码解析）

直接法是根据像素的亮度信息(Intensity）来估计相机的运动。

还记得估计相机的运动有以下方法：
1.提取特征点和描述子，比如SIFT，FAST特征点，不同视角的图片特征点匹配，然后用对极几何，PnP或ICP法估计相机运动。
2. 提取特征点，不提取描述子，然后用光流法跟踪特征点的运动，再估计相机运动。

而直接法可以在特征点的基础上计算，也可以连特征点都不提取了，直接随机采点。
也不用计算光流，不需要知道点和点之间的对应关系，而是通过最小化光度误差来得到，是一个优化问题。

直接法相比于特征点，克服了以下缺点，
1.提取特征点和描述子的计算很耗时。
2.使用特征点时，容易忽略特征点以外的信息。
3.没有明显纹理的地方，特征点有缺失。
4.光流法仍然需要特征点。

根据像素的使用数量，直接法有稀疏，稠密和半稠密3种。

直接法仍然基于灰度不变假设。

在光流法中，首先追踪特征点的位置，然后估计相机运动，是一个两步走的方案。
直接法是直接估计相机运动，通过优化相机位姿，寻找与点p1更相似的点p2，最小化目标是两个像素的亮度误差。

优化的步骤回忆一下高斯牛顿法，
首先把误差 $e$ 对相机运动 $T$ 求导，得到雅可比矩阵 $J$ ，
然后hessian矩阵H = JJ^T, b = -Je（e为误差），
再根据 $H\Delta x = b$ 求出更新量 $\Delta x$ ,
迭代，用 $\Delta x$ 更新 $T$ ，直到收敛。

上面的优化思路再具体一点：
首先，误差 $e = I_{1}(p_{1}) - I_{2}(p_{2})$ , $I$ 是Intensity,
终极目标是找到相机的运动 $T$ ,使 $\left\| e\right\|^{2}$ 最小。

假设一个点P在img1中的坐标为p1，在img2中的像素坐标为u
那么，
$e(T) = I_{1}(p_{1}) - I_{2}(u)$
而这个 $u$ 是根据相机内外参做如下转换而来的，
$q = T P$ ,? $\frac{1}{Z_{2}}Kq$
这个转换不重要，只需要知道q是T的函数，u是q的函数即可，因为后面用到导数的链式法则。

那么就开始用误差 $e$ 对相机的运动 $T$ 求导了，引入了李代数的左扰动模型，利用泰勒一阶展开：
$\frac{\partial e}{\partial T} = \frac{\partial I_{2}}{\partial u}\cdot \frac{\partial u}{\partial q}\cdot \frac{\partial q}{\partial \xi}$

其中 $\frac{\partial I_{2}}{\partial u}$ 是u处的像素梯度, 这里的u是坐标(u, v)。

而我们知道像素坐标(u,v) 和空间坐标(X, Y, Z)的关系（参考链接）
$f_{x}\frac{X}{Z} + c_{x}$ , ? $f_{y}\frac{Y}{Z} + c_{y}$
所以
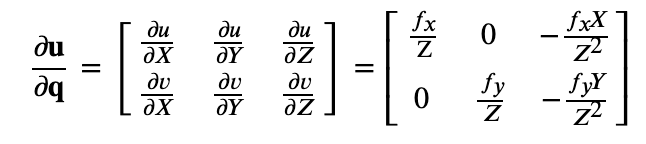
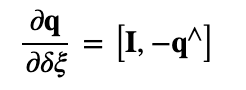
在这里插入图片描述

这是李代数的知识，这一步不用在意。

实际中，后两项只和q有关，与图像无关，合并到一起，得到。
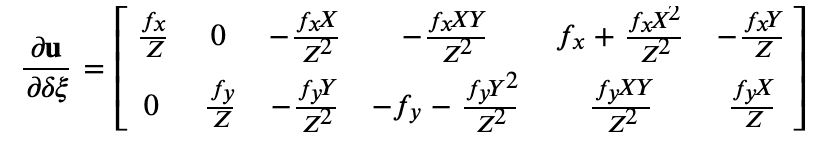
在这里插入图片描述
这个矩阵看着很吓人，实际用的时候，相机内参(fx, fy, cx, cy)已知，空间点坐标(X, Y, Z)已知的话，直接套公式可得。

不要忘了目标，我们的目标是求雅可比矩阵 $J$ ，
而 $\frac{\partial I_{2}}{\partial u}\cdot\frac{\partial u}{\partial \delta \xi}$
其实就是 1x2的像素梯度与一个2x6的矩阵相乘。

有了J就好办了，求H，b，解出更新量 $\Delta x$ ，不断更新相机运动 $T$ 直到收敛。

以上优化步骤体现在下面代码里

cv::Mat left_img = cv::imread(left_file, 0); //读入图片
//随机采2000个点（X,Y,Z)
for(int i = 0; i < nPoints; i++) {
    int x = rng.uniform(boarder, left_img.cols - boarder); //靠近边界的点不选
    int y = rng.uniform(boarder, left_img.rows - boarder);
    int disparity = disparity_img.at<uchar>(y, x); //是d，不是直接的深度哦
    double depth = fx * baseline / disparity;  //这个才是深度
    depth_ref.push_back(depth);
    pixels_ref.push_back(Eigen::Vector2d(x, y));
}
Sophus::SE3d T_cur_ref; //李群，旋转平移变换矩阵T
//直接法估计T
DirectPoseEstimationSingleLayer(left_img, img, pixels_ref, depth_ref, T_cur_ref);

来看下具体怎么估计T

void DirectPoseEstimationSingleLayer(
        const cv::Mat &img1,
        const cv::Mat &img2,
        const VecVector2d &px_ref,
        const vector<double> depth_ref,
        Sophus::SE3d &T21) {
    //迭代直到收敛    
    for(int iter = 0; iter < iterations; iter++) {
        jaco_accu.reset();
        //accumulate_jacobian在后面定义
        cv::parallel_for_(cv::Range(0, px_ref.size()),
                          std::bind(&JacobianAccumulator::accumulate_jacobian, &jaco_accu, placeholders::_1));
        Matrix6d H = jaco_accu.hessian();
        Vector6d b = jaco_accu.bias();

        // solve update and put it into estimation
        Vector6d update = H.ldlt().solve(b);
        T21 = Sophus::SE3d::exp(update) * T21; //exp:李代数到李群,se3:旋转平移变换T(R,t), *:T1*T2仍属于SE(3),乘法封闭性质
        cost = jaco_accu.cost_func();
        }

可以看到，上面的update就是我们要求的 $\Delta x$ , $\Delta x = H^{-1}\cdot b$
update求出来是李代数，而T是李群，用se3.exp(update)把update转到李群。由于李群是乘法封闭性质，se3.exp(update)并不是加到T上，而是用se3.exp(update) * T

parallel_for_并行计算J，H和b，具体如下

//并行计算这么多点
    for(size_t i = range.start; i < range.end; i++) {
        // compute the projection in the second image
        //像素坐标转相机坐标:u=fx(X/Z) + cx => X = Z * ((u - cx)/fx)
        Eigen::Vector3d point_ref =
                depth_ref[i] * Eigen::Vector3d((px_ref[i][0] - cx) / fx, (px_ref[i][1] - cy) / fy, 1);
        Eigen::Vector3d point_cur = T21 * point_ref;  //T21:上面算出来的旋转平移变换矩阵,得到相机位姿变化后点的相机坐标
        if(point_cur[2] < 0) continue;  //深度无效

        //相机坐标到像素坐标：u=fx(X/Z) + cx
        float u = fx * point_cur[0] / point_cur[2] + cx;
        float v = fy * point_cur[1] / point_cur[2] + cy;
        if(u < half_patch_size || u > img2.cols - half_patch_size || v < half_patch_size ||
        v > img2.rows - half_patch_size) continue;  //无效点

        projection[i] = Eigen::Vector2d(u, v);  //像素坐标
        double X = point_cur[0], Y = point_cur[1], Z = point_cur[2]; //相机坐标
        double Z2 = Z * Z, Z_inv = 1.0 / Z, Z2_inv = Z_inv * Z_inv; //提前计算
        cnt_good ++;  //有效点个数

        //单个点找对应点误差大，用一片patch
        for(int x = -half_patch_size; x <= half_patch_size; x++) {
            for(int y = -half_patch_size; y <= half_patch_size; y++) {
                //img1的像素和img2对应像素的一片patch内的intensity误差
                double error = GetPixelValue(img1, px_ref[i][0] + x, px_ref[i][1] + y) -
                        GetPixelValue(img2, u + x, v + y);
                Matrix26d J_pixel_xi; //变换后的三维点对变换T的左扰动的导数，2x6矩阵
                Eigen::Vector2d J_img_pixel; //图像对像素点的导数

                //套公式
                J_pixel_xi(0, 0) = fx * Z_inv;
                J_pixel_xi(0, 1) = 0;
                J_pixel_xi(0, 2) = -fx * X * Z2_inv;
                J_pixel_xi(0, 3) = -fx * X * Y * Z2_inv;
                J_pixel_xi(0, 4) = fx + fx * X * X * Z2_inv;
                J_pixel_xi(0, 5) = -fx * Y * Z_inv;

                J_pixel_xi(1, 0) = 0;
                J_pixel_xi(1, 1) = fy * Z_inv;
                J_pixel_xi(1, 2) = -fy * Y * Z2_inv;
                J_pixel_xi(1, 3) = -fy - fy * Y * Y * Z2_inv;;
                J_pixel_xi(1, 4) = fy * X * Y * Z2_inv;
                J_pixel_xi(1, 5) = fy * X * Z_inv;

                //图像对像素的导数为(u, v)处的像素梯度
                J_img_pixel = Eigen::Vector2d(
                        0.5 * (GetPixelValue(img2, u+1+x, v+y) - GetPixelValue(img2, u-1+x, v+y)),
                        0.5 * (GetPixelValue(img2, u+x, v+1+y) - GetPixelValue(img2, u+x, v-1+y))
                        );

                //根据导数的链式法则, (1x2) x (2x6) = (1x6) -> (6x1)
                Vector6d J = -1.0 * (J_img_pixel.transpose() * J_pixel_xi).transpose();

                //高斯牛顿
                hessian += J * J.transpose();
                bias += -error * J;
                cost_tmp += error * error;
            }
        }
        //一块patch求完
        if(cnt_good) {
            unique_lock<mutex> lck(hessian_mutex); //多线程锁,在block结束时自动释放
            H += hessian;
            b += bias;
            cost += cost_tmp / cnt_good;
        }
    }

上面就是优化相机运动 $T$ 的步骤，
再来说下图像金字塔直接法，它是coarse to fine的思想，金字塔从下到上对图像进行缩放。
需要注意的是图像缩放的同时，相机内参和点的坐标也要一起缩放。
计算时从上层计算，每层的结果传入下面一层作为参考值，见代码

    //create pyramids
    vector<cv::Mat> pyr1, pyr2;
    //装入图像金字塔
    for(int i = 0; i < pyramids; i++) {
        if(i == 0) {
            pyr1.push_back(img1);
            pyr2.push_back(img2);
        } else {
            cv::Mat img1_pyr, img2_pyr;
            cv::resize(pyr1[i-1], img1_pyr,
                       cv::Size(pyr1[i-1].cols * pyramid_scale, pyr1[i-1].rows * pyramid_scale));
            cv::resize(pyr2[i-1], img2_pyr,
                       cv::Size(pyr2[i-1].cols * pyramid_scale, pyr2[i-1].rows * pyramid_scale));
            pyr1.push_back(img1_pyr);
            pyr2.push_back(img2_pyr);
        }
    }

    double fxG = fx, fyG = fy, cxG = cx, cyG = cy; //相机内参也要随着金字塔一起缩放，先backup原值
    for(int level = pyramids - 1; level >= 0; level --) { //金字塔从顶层到底层处理
        VecVector2d px_ref_pyr;  //当前层的keypoints
        for(auto &px : px_ref) {
            px_ref_pyr.push_back((scales[level] * px)); //特征点的坐标也要缩放
        }

        //缩放的相机内参
        fx = fxG * scales[level];
        fy = fyG * scales[level];
        cx = cxG * scales[level];
        cy = cyG * scales[level];
        //px_ref_pyr, T21是引用形参，下一层会基于上一层的结果进行计算
        DirectPoseEstimationSingleLayer(pyr1[level], pyr2[level], px_ref_pyr, depth_ref, T21);
    }