[人工智能] 深蓝-视觉slam-第二讲习题

开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 深蓝-视觉slam-第二讲习题 -> 正文阅读

[人工智能]深蓝-视觉slam-第二讲习题

1，熟悉Eigen矩阵运算
在这里插入图片描述
（1）A系数矩阵的秩（R）和增广矩阵（A,b）的秩相同。
行阶梯型矩阵：非零矩阵若满足非零行在零行的上面；非零行的首非零元所在的列在上一行的首非零元所在列的后面，则称此矩阵为行阶梯形矩阵；
R——秩就是矩阵非零子式的最高阶数，将A和B=（A，b)经过初等行变换变成行阶梯形矩阵，如若R(A) = R(B) = n,则说明线性方程组有唯一解。
在这里插入图片描述
（2)高斯消元法：线性代数用于求解线性方程组的算法，通过求解可以求出矩阵的秩，以及可逆矩阵的逆矩阵

以下行列式的性质，将增广矩阵变为行阶梯形矩阵（简单的三角形式）：

对换行列式的两行（列），行列式变号；
行列式的某一行（列）值中的所有元素都乘以同一常数k，等与用k乘以此行列和式；
把行列式的某一行（列）的各元素乘同一数然后加到另一行（列）对应的元素上去，行列式不变；
1）线性方程组：

2）构造增广矩阵(A,b):

3）通过行列式初等变换后的方程组形式：简单的三角方阵组；
请添加图片描述
4）通过前后替换算法求解x,y,z: 下三角矩阵的前向替换和上三角矩阵的反向替换的迭代过程来解决
对于上三角形：先知道z的值，然后带入上一行求出y，然后将y,z带入上一行，可得解；
z=-4/-4=1, y=4-2z=4-2=2, x= (1-y-z)/2=(1-2-1)/2=-1

（3）QR分解的原理：
施密特正交化：从线性无关向量组a2,a2,…ar导出正交向量组b1,b2…bn的过程。
在这里插入图片描述

上式来解释下式中K21，K31等系数的由来：
酋矩阵是正交矩阵在复数上的推广

（3）Cholesky分解：
先简单的理解一下正定矩阵和半正定矩阵：

给定一个n x n 的实对称矩阵A，若对于任意长度的非零向量X，有 $\mathbf{x}^\intercal$ $\mathbf{A}$ $\mathbf{x}$ > 0恒成立，则矩阵A是一个正定矩阵。
给定一个n x n 的实对称矩阵A，若对于任意长度的非零向量X，有 $\mathbf{x}^\intercal$ $\mathbf{A}$ $\mathbf{x}$ > =0恒成立，则矩阵A是一个半正定矩阵。

若 $\mathbf{A}$ 为正定矩阵，则可将其分解为： $\mathbf{A}$ = $\mathbf{L}$ $\mathbf{L}^\intercal$
在这里插入图片描述
L为下三角矩阵， $\mathbf{L}^\intercal$ 为L矩阵的转置矩阵上三角矩阵，L可表示为：

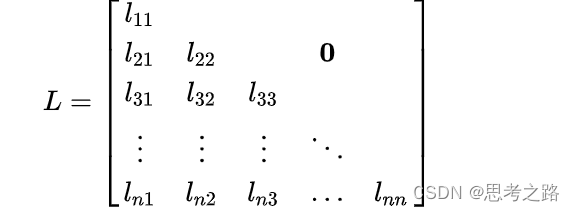
由于 $\mathbf{A}$ 矩阵可以将其拆分为 $\mathbf{L}$ $\mathbf{L}^\intercal$ 的形式，所以 $\mathbf{A}$ 矩阵中的元素可以由 $\mathbf{L}$ $\mathbf{L}^\intercal$ 中的值等价：将矩阵关系 $\mathbf{A}$ = $\mathbf{L}$ $\mathbf{L}^\intercal$ 展开，有
在这里插入图片描述
由上式子可以得出L的元素：,计算公式为：
对于正定方程组Ax = b可以由 $\mathbf{L}$ y = b和 $\mathbf{L}^\intercal$ x = y 来求解，由Ly = b：

在这里插入图片描述通过上式可以顺序计算出y1 ——>y2——>y3…——>yn:

由 $\mathbf{L}^\intercal$ x = y ：

可逆序求出：xn…x3——>x2——>x1:

(5)Eigen固定大小矩阵最大支持到50
eigenMatrix.cpp:

#include <Eigen/Core>
#include <Eigen/Dense>
#include <Eigen/Geometry>
#include <ctime>
#include <iostream>
using namespace std;
using namespace Eigen;
#define MATRIX_SIZE 100

int main(int argc, char **argv) {
  Matrix<double, MATRIX_SIZE, MATRIX_SIZE> matrix_NN =
      MatrixXd::Random(MATRIX_SIZE, MATRIX_SIZE);
  matrix_NN = matrix_NN * matrix_NN.transpose();  // 保证半正定
  Matrix<double, MATRIX_SIZE, 1> v_Nd = MatrixXd::Random(MATRIX_SIZE, 1);
  clock_t time_stt = clock();  // 计时
  // 通常用矩阵分解来求，例如QR分解，速度会快很多
  Matrix<double, MATRIX_SIZE, 1> x = matrix_NN.inverse() * v_Nd;

  x = matrix_NN.colPivHouseholderQr().solve(v_Nd);
  cout << "time of Qr decomposition is "
       << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;
  cout << "x = " << x.transpose() << endl;

  // 对于正定矩阵，还可以用cholesky分解来解方程
  time_stt = clock();
  x = matrix_NN.ldlt().solve(v_Nd);
  cout << "time of ldlt decomposition is "
       << 1000 * (clock() - time_stt) / (double)CLOCKS_PER_SEC << "ms" << endl;
  cout << "x = " << x.transpose() << endl;

  return 0;
}

CMakeLists.txt:

cmake_minimum_required(VERSION 3.4)
project(useQReigen)

set(CMAKE_BUILD_TYPE "Release")
set(CMAKE_CXX_FLAGS "-O3")

# 添加Eigen头文件
include_directories("/usr/include/eigen3")
add_executable(eigenMatrix eigenMatrix.cpp)

运行结果：
在这里插入图片描述
2.矩阵论基础

在这里插入图片描述
（1）正定矩阵和半正定矩阵：

给定一个n x n 的实对称矩阵A，若对于任意长度的非零向量X，有 $\mathbf{x}^\intercal$ $\mathbf{A}$ $\mathbf{x}$ > 0恒成立，则矩阵A是一个正定矩阵。
给定一个n x n 的实对称矩阵A，若对于任意长度的非零向量X，有 $\mathbf{x}^\intercal$ $\mathbf{A}$ $\mathbf{x}$ > =0恒成立，则矩阵A是一个半正定矩阵。

（2）设 $\mathbf{A}$ 是n阶矩阵，如果数 $\lambda$ 和n维非零列向量x使关系式 $\mathbf{A}$ x = $\lambda$ x成立，那么，这样的数 $\lambda$ 就是 $\mathbf{A}$ 矩阵的特征值，非零向量x就是 $\mathbf{A}$ 的特征值对应的特征向量
( $\mathbf{A}$ - $\lambda$ E) x = 0 ,这是个n个未知数n个方程的齐次线性方程组，它有非零解的充分必要条件是系数行列式等于0：
| $\mathbf{A}$ - $\lambda$ E| = 0
下面例题可以说明方阵的特征值和特征向量：在这里插入图片描述
n阶矩阵的特征值不一定都是实数，只有对称矩阵的特征值才保证是实数。
（3）设A，B都是n阶矩阵，若有可逆矩阵P，使得
则称B是A的相似矩阵，对A进行运算称为对A进行相似变换，P称为把A变成B的相似变换矩阵。
矩阵的相似性反映的几何意义：https://www.zhihu.com/question/25352258
在基底（e1,e2)下，坐标为x的向量通过矩阵A完成了线性变换，线性变换后的坐标为x’，我们也可以通过矩阵P，将向量变换到（e1’,e2’)下的坐标，即用新的基底下的坐标来表示向量，记作Px.这时在新的基底下，用来表示我们上面同一个空间变换的是另一个坐标B，即基底（e1’,e2’)下变换后的目标坐标为BPx,最后我们还是需要在原基底坐标系下讨论和比较问题，把坐标从基地（e1’,e2’)回到（e1,e2)下，这个个逆变换，即左乘一个逆矩阵P的逆和之前的A变换一样了。
（4）不一定，实对称矩阵一定能对角化
在这里插入图片描述
不能对角化的矩阵能够形成（Jordan标准形）

示例了解矩阵不能对角化后是如何化成Jordan标准形的：参考：http://staff.ustc.edu.cn/~mathsu01/note/pdf/2020autumn/xxdsA2%20chen%206.6-7.6.pdf

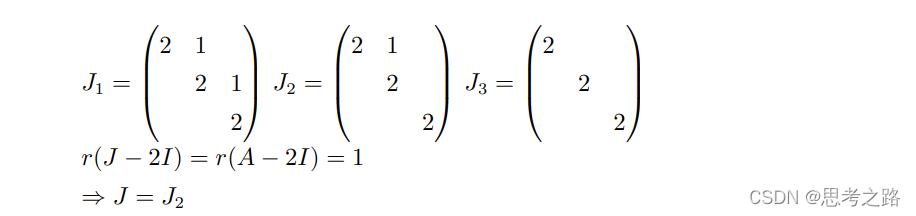
（5）奇异值分解（SVD）

SVD的定义：SVD是对矩阵进行分解，SDV并不要求要分解的矩阵为方阵。A是一个m x n的矩阵，我们定义矩阵A的SVD为： $\mathbf{A}$ = $\mathbf{U}$ $\mathbf{Σ}$ $\mathbf{V}^\intercal$
其中U是一个mxm的矩阵，Σ是一个mxn的矩阵，除了主对角线的元素外全为0，主对角线上的每个元素称为奇异值，V是一个nxn的矩阵。U和V都是酉矩阵，即满足 $\mathbf{U}^\intercal$ $\mathbf{U}$ = $\mathbf{I}$ , $\mathbf{V}^\intercal$ $\mathbf{V}$ = $\mathbf{I}$ ,下面是对SVD形象的定义：
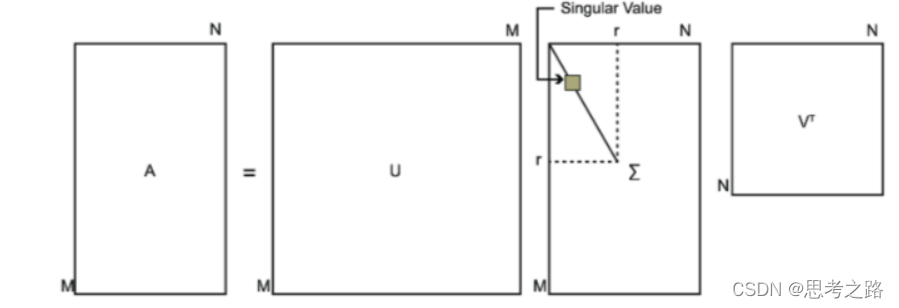
在这里插入图片描述
我们如何求解SVD分解后的U，V，Σ呢？

将A的转置与A乘积得到n x n 的方阵，然后进行特征值分解，得到特征值和特征向量满足如下等式：
( $\mathbf{A}^\intercal$ $\mathbf{A}$ )vi=λivi
这样我们就得到了 $\mathbf{A}^\intercal$ $\mathbf{A}$ 的n个特征值和特征值对应的特征向量v了，将所有的特征向量组成一个nxn的矩阵V，就是SVD公式里的V 矩阵了，将V中的每个特征向量叫做A的右奇异向量。

将A和A的转置作乘法，得到mxm的方阵，然后经进行特征置分解，得到特征值和特征向量满足如下等式：
( $\mathbf{A}$ $\mathbf{A}^\intercal)$ ui=λiui 我们就得到了m个特征值和对应的特征向量了，将 $\mathbf{A}$ $\mathbf{A}^\intercal$ 的所有特征向量组成一个mxm的矩阵U，这就是SVD里的U矩阵了，U中的特征向量叫做A的左奇异向量。
U和V求出来了，现在就是求Σ，除了对角线上元素不为0，其余都为0，只需求出奇异值σ
A=UΣVT?AV=UΣVTV?AV=UΣ?Avi=σiui?σi=Avi/ui 这样我们可以求出我们的每个奇异值，进而求出奇异值矩阵Σ。
　上面还有一个问题没有讲，就是我们说ATA的特征向量组成的就是我们SVD中的V矩阵，而AAT的特征向量组成的就是我们SVD中的U矩阵，这有什么根据吗？这个其实很容易证明，我们以V矩阵的证明为例。
A=UΣVT?AT=VΣTUT?ATA=VΣTUTUΣVT=VΣ2VT。　上式证明使用了:UTU=I,ΣTΣ=Σ2。可以看出ATA的特征向量组成的的确就是我们SVD中的V矩阵。类似的方法可以得到AAT的特征向量组成的就是我们SVD中的U矩阵。

进一步我们还可以看出我们的特征值矩阵等于奇异值矩阵的平方，也就是说特征值和奇异值满足如下关系：
σi=λi??√
　　　　这样也就是说，我们可以不用σi=Avi/ui来计算奇异值，也可以通过求出ATA的特征值取平方根来求奇异值。
　　　　在这里插入图片描述
（6）伪逆：如果A的秩不为0，则A可以进行满秩分解A = FG ，那么A的伪逆：

P是线性代数中常用的投影矩阵，只有当U的列向量是线性无关的时候，才可以求P，该矩阵的作用就是将任何向量x投影到U的列量量的空间上。
多数线性方程组Ax = b,没有精确的解，因为b不在A的列空间中，
因此只能在A的列空间中找一个和b欧式距离最小的b’，b’就是b投影到A的列空间上的结果，即在这里插入图片描述
而我们希望求解这样一个x’，使得
x’就是最小误差的二范数的解，对上式左右两边乘以得到

接下来就是求解该方程的一个最小二范数解，只要将任何一个特解x0,投影到G的行空间即可得到最小二范数解，用F代替P中的U即可得到投影到F列空间的变换矩阵，但我们现在要投影到G的行空间上，所以用G的转置带入到P中，得到：
在这里插入图片描述
那么最终得到的解就是：
x0是特解，这就意味着

因此：在这里插入图片描述
（7）
（a）因为A不可逆，当b不等于0时，增广矩阵的秩和系数矩阵的秩不相等，方程没有解析解，所以可以计算最小二乘解，使得方程两边的误差平方的和为最小的解，此时最小二乘的形式：x = (ATA)的逆乘以A的转置再乘以b.
A的奇异值是A的转置乘以A的特征值的平方根

（b)当b=0时，相当与求超定齐次方程组Ax = 0 解，最小二乘解就是A的SVD分解后V的最后一个列向量，还等于A的转置乘以A的最小特征值对应的特征向量
（c）对于任何超定的线性方程Ax = b都是有最小二乘解的，系数矩阵与变量列向量相乘本质上就是矩阵列向量的线性组合，而向量的每个元素都是系数。因此线性方程的列向量将长成一个多位列空间S，而向量b不在这个空间上，虽然b不在矩阵A的列空间S上，也就是说找不到一组x的系数使得Ax = b，但可以在列空间S上找到一个向量b’，满足Ax’ = b’，使得向量b-b’的长度最小，这个线性组合的系数x’就是最小二乘解，当b-b’垂直与S空间时，得到最小二乘解。向量b’就是b在A的列空间上的投影。如果b与A的列空间S垂直，那么最小二乘就是n维0向量。
p向量是b向量在S平面上的投影。
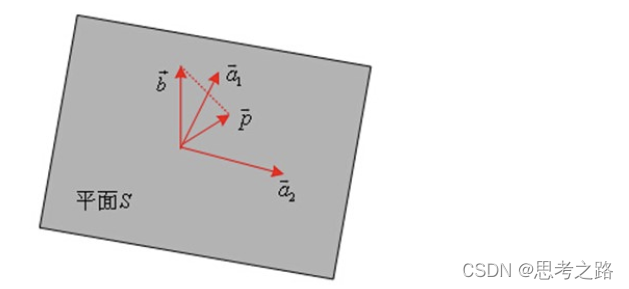
在这里插入图片描述

3.几何运算练习
在这里插入图片描述
(1).由于题目中给出的坐标系变化形式是：四元数 + 平移，四元数代表了坐标系的旋转，所以不同坐标系下的变换可以用变换矩阵（T)来描述。激光传感器下看到的点记作pL，要计算它在世界坐标系的坐标，需要将计算出依次在B系下，R系下，W系下的坐标即可；
pW = TWR . TRB .TBL . pL
(2). 四元数在使用前需要归一化,设相机坐标系下的点记作p;
（a).激光系下的坐标：将相机系下看到的坐标变换到和激光传感器共同的标定系下(B),然后在将其变换到激光系下的坐标即可；
q = TBL.inverse() * TBC * p;
（b).世界坐标系下的坐标：由于观测到的点是在相机传感器系（C)下看到的坐标点，要计算该点在世界坐标系下的坐标，需要先将该点在B系，R系，W系下的坐标求出，即可；
q = TWR * TRB * TBC * p;
（c).代码如下：

#include<Eigen/Core>
#include<Eigen/Geometry>
#include<iostream>
using namespace std;
using namespace Eigen;

int main(int argc,char** argv[])
{
        Quaterniond qWR(0.55,0.3,0.2,0.2),qRB(0.99,0,0,0.01),qBL(0.3,0.5,0,20.1),qBC(0.8,0.2,0.1,0.1);
        qWR.normalize();
        qRB.normalize();
        qBL.normalize();
        qBC.normalize();

        Vector3d tWR(0.1,0.2,0.3),tRB(0.05,0,0.5),tBL(0.4,0,0.5), tBC(0.5,0.1,0.5);
        Vector3d p(0.3,0.2,1.2);

        Isometry3d Twr(qWR), Trb(qRB),Tbl(qBL), Tbc(qBC);
        Twr.pretranslate(tWR);
        Trb.pretranslate(tRB);
        Tbl.pretranslate(tBL);
        Tbc.pretranslate(tBC);

        Vector3d q = Tbl.inverse() * Tbc * p;
        cout << "激光坐标系下的坐标为：" << q.transpose() << endl;

         q = Twr * Trb * Tbc * p;
        cout << "世界坐标系下的坐标为:" << q.transpose() << endl;
        return 0;

}

运行结果：
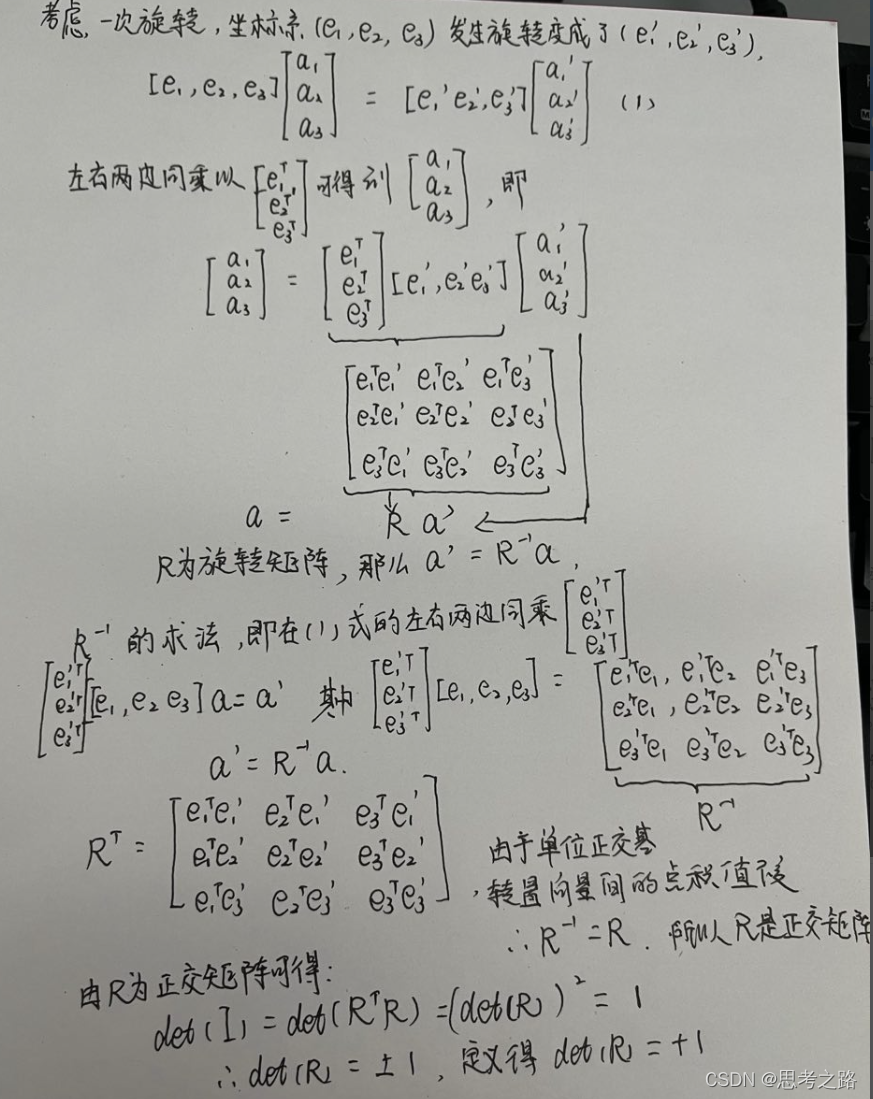
在这里插入图片描述
4，旋转的表达

（1）
（2）四元数：表示了三维空间的旋转，是一种类似与复数的代数，由实部和虚部组成，ε是三维度的，η是一维度的
（3）

5，罗德里格斯公式的证明
参考：https://blog.csdn.net/q583956932/article/details/78933245
在这里插入图片描述
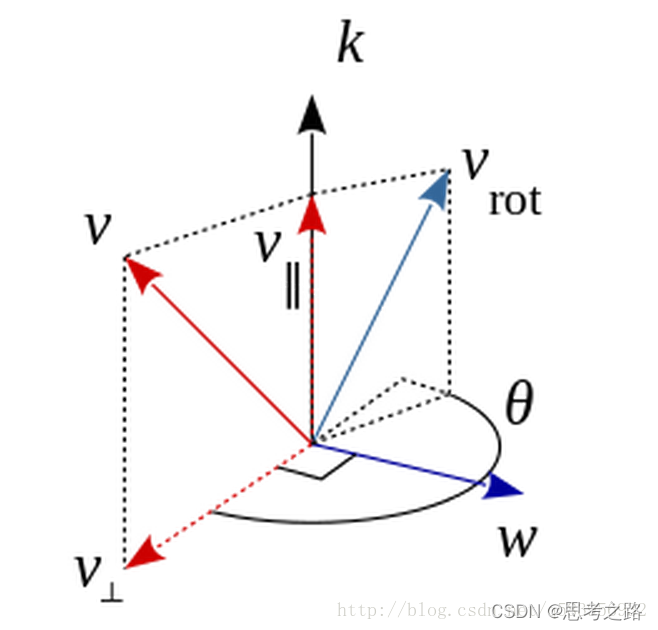
请添加图片描述

6，四元数运算性质的验证

7，熟悉C++11

(1)auto 可以在声明变量时根据变量初始化值的类型自动为此变量选择匹配的类型。
（2）c++标准中，为for循环添加了一种全新的语法格式：

	for (declaration : expression){
	    //循环体
	}

**declaration:**表示此处要定义一个变量，该变量的类型为要遍历序列中存储元素的类型。c++标准中，declaration参数处定义的变量类型可以用auto关键字表示，该关键字可以使编译器自行推导该变量的数据类型。
**expression:**表示要遍历的序列，常见的可以为事先定义好的普通数组或容器，还可以是{}大括号初始化的序列。
（3）Lambda表达式
lambda表达式类似于javascript中的闭包，它可以用于创建并定义匿名的函数对象，以间化编成工作。lambda提供了一个类似匿名函数的特性，而匿名函数则是在需要一个函数，但是又不想费力去命名一个函数名的晴空下的使用
语法： [函数对象参数](操作符重载函数参数]->返回值类型{函数体}

vector<int> iv{5, 4, 3, 2, 1};
int a = 2, b = 1;
for_each(iv.begin(), iv.end(), [b](int &x){cout<<(x + b)<<endl;}); // (1)
for_each(iv.begin(), iv.end(), [=](int &x){x *= (a + b);}); // (2)
for_each(iv.begin(), iv.end(), [=](int &x)->int{return x * (a + b);});//
(3)

[]内的参数指的是Lambda表达式可以取得的全局变量。(1)函数中的b就是指函数可以得
到在Lambda表达式外的全局变量，如果在[]中传入=的话，即是可以取得所有的外部变
量，如（2）和（3）Lambda表达式()内的参数是每次调用函数时传入的参数。->后加上的是Lambda表达式返回值的类型，如（3）中返回了一个int类型的变量