文章目录
参考资料
本博客为作者根据周志华的西瓜书和参考资料1、2、3所做的笔记,主要用于学习,非技术类博客,因此存在大量复制粘贴,请见谅。
如果本篇博客有后记部分,则该部分表示的是在书本原有的基础知识上,进行的知识点的扩充。
1. 基本概念
贝叶斯决策论(Bayesian decision theory)是概率框架下实施决策的基本方法,对分类任务来说,在所有相关概率都已知的理想情形下,贝叶斯决策论考虑如何基于这些概率和误判损失来选择最优的类别标记。
1.1 贝叶斯公式

1.2 贝叶斯决策论
假设有N种可能的类别标记,即 y = [ c 1 , c 2 , . . . , c N ) y=[c_1,c_2,...,c_N) y=[c1?,c2?,...,cN?), λ i j \lambda_{ij} λij?是将一个真实标记为 c j c_j cj?的样本误分类为 c i c_i ci?所产生的损失,基于后验概率 P ( c i ∣ x ) P(c_i|x) P(ci?∣x)可获得将样本 x x x分类为 c i c_i ci?所产生的期望损失(expected loss),即在样本 x x x上的“条件风险”(conditional risk)
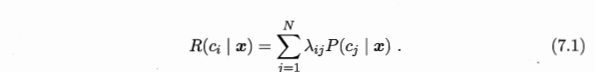
决策论中将“期望损失”称为“风险” (risk).
我们的任务就是寻找一个判定准则最小化所有样本的条件风险总和,因此就有了贝叶斯判定准则(Bayes decision rule):为最小化总体风险,只需在每个样本上选择那个使得条件风险最小的类标。

此时, h ? h^* h?称为贝叶斯最优分类器(Bayes optimal classifier),与之对应的总体风险 R ( h ? ) R(h^*) R(h?)称为贝叶斯风险(Bayes risk). 1 ? R ( h ? ) 1-R(h^*) 1?R(h?)反映了分类器所能达到的最好性能,即通过机器学习所能产生的模型精度的理论上限.
具体来说,若目标是最小化分类错误率,则误判损失可写为0-1损失:
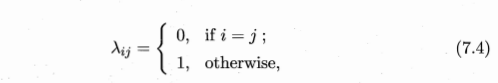

即对于每个样本x,选择其后验概率 P ( c ∣ x ) P(c | x) P(c∣x)最大所对应的类标,能使得总体风险函数最小,从而将原问题转化为估计后验概率 P ( c ∣ x ) P(c | x) P(c∣x)。一般这里有两种策略来对后验概率进行估计:
- 判别式模型:直接对 P ( c ∣ x ) P(c | x) P(c∣x)进行建模求解。例我们前面所介绍的决策树、神经网络、SVM都是属于判别式模型。
- 生成式模型:通过先对联合分布 P ( c ∣ x ) P(c | x) P(c∣x)建模,从而进一步求解 P ( c ∣ x ) P(c | x) P(c∣x)。
判别模型(discriminative model)通过求解条件概率分布或者直接计算y的值来预测y。
线性回归(Linear Regression),逻辑回归(Logistic Regression),支持向量机(SVM), 传统神经网络(Traditional Neural Networks),线性判别分析(Linear Discriminative Analysis),条件随机场(Conditional Random Field)
生成模型(generative model)通过对观测值和标注数据计算联合概率分布来达到判定估算y的目的。
朴素贝叶斯(Naive Bayes), 隐马尔科夫模型(HMM),贝叶斯网络(Bayesian Networks)和隐含狄利克雷分布(Latent Dirichlet Allocation)、混合高斯模型
贝叶斯分类器就属于生成式模型,基于贝叶斯公式对后验概率
P
(
c
∣
x
)
P(c | x)
P(c∣x) 进行一项变换:

对于给定的样本x, P ( x ) P(x) P(x)与类标无关, P ( c ) P(c) P(c)称为类先验概率, P ( x ∣ c ) P(x | c ) P(x∣c)称为类条件概率。这时估计后验概率 P ( c ∣ x ) P(c | x) P(c∣x)就变成为估计类先验概率和类条件概率的问题。
对于先验概率和后验概率,这里普及一下它们的基本概念。
- 先验概率: 根据以往经验和分析得到的概率。
- 后验概率:后验概率是基于新的信息,修正原来的先验概率后所获得的更接近实际情况的概率估计。直观意义上后验概率就是条件概率。
对于类先验概率 P ( c ) P(c) P(c), P ( c ) P(c) P(c)就是样本空间中各类样本所占的比例,根据大数定理(当样本足够多时,频率趋于稳定等于其概率),这样当训练样本充足时, P ( c ) P(c) P(c)可以使用各类出现的频率来代替。因此只剩下类条件概率 P ( x ∣ c ) P(x | c ) P(x∣c),它表达的意思是在类别c中出现x的概率,它涉及到属性的联合概率问题,若只有一个离散属性还好,当属性多时采用频率估计起来就十分困难,因此这里一般采用极大似然法进行估计。
1.3 极大似然法
极大似然估计(Maximum Likelihood Estimation,简称MLE),是一种根据数据采样来估计概率分布的经典方法。
常用的策略是先假定总体具有某种确定的概率分布,再基于训练样本对概率分布的参数进行估计。
运用到类条件概率 P ( x ∣ c ) P(x | c ) P(x∣c)中,假设 P ( x ∣ c ) P(x | c ) P(x∣c)服从一个参数为θ的分布,问题就变为根据已知的训练样本来估计θ。
极大似然法的核心思想就是:估计出的参数使得已知样本出现的概率最大,即使得训练数据的似然最大。

所以,贝叶斯分类器的训练过程就是参数估计。总结最大似然法估计参数的过程,一般分为以下四个步骤:
- 写出似然函数;
- 对似然函数取对数,并整理;
- 求导数,令偏导数为0,得到似然方程组;
- 解似然方程组,得到所有参数即为所求。
例如:假设样本属性都是连续值, P ( x ∣ c ) P(x | c ) P(x∣c)服从一个多维高斯分布,则通过MLE计算出的参数刚好分别为:

上述结果看起来十分合乎实际,但是采用最大似然法估计参数的效果很大程度上依赖于作出的假设是否合理,是否符合潜在的真实数据分布。
2. 朴素贝叶斯分类器
原始的贝叶斯分类器最大的问题在于联合概率密度函数的估计,首先需要根据经验来假设联合概率分布,其次当属性很多时,训练样本往往覆盖不够,参数的估计会出现很大的偏差。
为了避免这个问题,朴素贝叶斯分类器(naive Bayes classifier)采用了“属性条件独立性假设”,即样本数据的所有属性之间相互独立。这样类条件概率
P
(
x
∣
c
)
P(x | c )
P(x∣c)可以改写为:


这样,为每个样本估计类条件概率变成为每个样本的每个属性估计类条件概率。

相比原始贝叶斯分类器,朴素贝叶斯分类器基于单个的属性计算类条件概率更加容易操作,需要注意的是:若某个属性值在训练集中和某个类别没有一起出现过,这样会抹掉其它的属性信息,因为该样本的类条件概率被计算为0。因此在估计概率值时,常常用进行平滑(smoothing)处理,拉普拉斯修正(Laplacian correction)就是其中的一种经典方法,具体计算方法如下:

当训练集越大时,拉普拉斯修正引入的影响越来越小。对于贝叶斯分类器,模型的训练就是参数估计,因此可以事先将所有的概率储存好,当有新样本需要判定时,直接查表计算即可。
朴素贝叶斯朴素在哪里呢? —— 两个假设:
- 一个特征出现的概率与其他特征(条件)独立;
- 每个特征同等重要。
3. 半朴素贝叶斯分类器
朴素贝叶斯分类器采用了属性条件独立性假设,但在现实任务中这个假设往往很难成立,于是,人们尝试对属性条件独立性假设进行一定程度的放松,由此产生了一类称为“半朴素贝叶斯分类器”(semi-naive Bayes classifiers)的学习方法.
半朴素贝叶斯分类器的基本想法是适当考虑一部分属性间的相互依赖信息,从而既不需进行完全联合概率计算,又不至于彻底忽略了比较强的属性依赖关系.
“独依赖估计” (One-Dependent Estimator,简称 ODE)是半朴素贝叶斯分类器最常用的一种策略,顾名思义,所谓“独依赖”就是假设每个属性在类别之外最多仅依赖于一个其他属性,即

4. EM算法
EM(Expectation-Maximization)算法是一种常用的估计参数隐变量的利器,也称为“期望最大算法”,是数据挖掘的十大经典算法之一。EM算法主要应用于训练集样本不完整即存在隐变量时的情形(例如某个属性值未知),通过其独特的“两步走”策略能较好地估计出隐变量的值。
4.1 EM算法思想
EM是一种迭代式的方法,它的基本思想就是:若样本服从的分布参数θ已知,则可以根据已观测到的训练样本推断出隐变量Z的期望值(E步),若Z的值已知则运用最大似然法估计出新的θ值(M步)。重复这个过程直到Z和θ值不再发生变化。
简单来讲:假设我们想估计A和B这两个参数,在开始状态下二者都是未知的,但如果知道了A的信息就可以得到B的信息,反过来知道了B也就得到了A。可以考虑首先赋予A某种初值,以此得到B的估计值,然后从B的当前值出发,重新估计A的取值,这个过程一直持续到收敛为止。

现在再来回想聚类的代表算法K-Means(后面的章节会提到):首先随机选择类中心=>将样本点划分到类簇中=>重新计算类中心=>不断迭代直至收敛,不难发现这个过程和EM迭代的方法极其相似,事实上,若将样本的类别看作为“隐变量”(latent variable)Z,类中心看作样本的分布参数θ,K-Means就是通过EM算法来进行迭代的,与我们这里不同的是,K-Means的目标是最小化样本点到其对应类中心的距离和,上述为极大化似然函数。
4.2 EM算法数学推导
当样本属性值都已知时,我们很容易通过极大化对数似然,接着对每个参数求偏导计算出参数的值。但当存在隐变量时,就无法直接求解,此时我们通常最大化已观察数据的对数“边际似然”(marginal likelihood)。
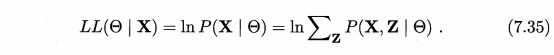
这时候,通过边缘似然将隐变量Z引入进来,对于参数估计,现在与最大似然不同的只是似然函数式中多了一个未知的变量Z,也就是说我们的目标是找到适合的θ和Z让L(θ)最大,这样我们也可以分别对未知的θ和Z求偏导,再令其等于0。
然而观察上式可以发现,和的对数(ln(x1+x2+x3))求导十分复杂,那能否通过变换上式得到一种求导简单的新表达式呢?这时候 Jensen不等式就派上用场了,先回顾一下高等数学凸函数的内容:
Jensen’s inequality:过一个凸函数上任意两点所作割线一定在这两点间的函数图象的上方。理解起来也十分简单,对于凸函数 f ( x ) ′ ′ f(x)'' f(x)′′>0,即曲线的变化率是越来越大单调递增的,所以函数越到后面增长越厉害,这样在一个区间下,函数的均值就会大一些了。
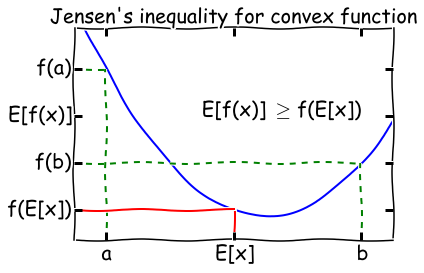
因为ln(*)函数为凹函数,故可以将上式“和的对数”变为“对数的和”,这样就很容易求导了。

接着求解 Q i Q_i Qi?和θ:首先固定θ(初始值),通过求解 Q i Q_i Qi?使得 J ( θ , Q ) J(θ,Q) J(θ,Q)在θ处与L(θ)相等,即求出 L ( θ ) L(θ) L(θ)的下界;然后再固定 Q i Q_i Qi?,调整θ,最大化下界 J ( θ , Q ) J(θ,Q) J(θ,Q)。不断重复两个步骤直到稳定。通过jensen不等式的性质, Q i Q_i Qi?的计算公式实际上就是后验概率:

通过数学公式的推导,简单来理解这一过程:固定θ计算Q的过程就是在建立 L ( θ ) L(θ) L(θ)的下界,即通过jenson不等式得到的下界(E步);固定Q计算θ则是使得下界极大化(M步),从而不断推高边缘似然 L ( θ ) L(θ) L(θ)。从而循序渐进地计算出 L ( θ ) L(θ) L(θ)取得极大值时隐变量Z的估计值。
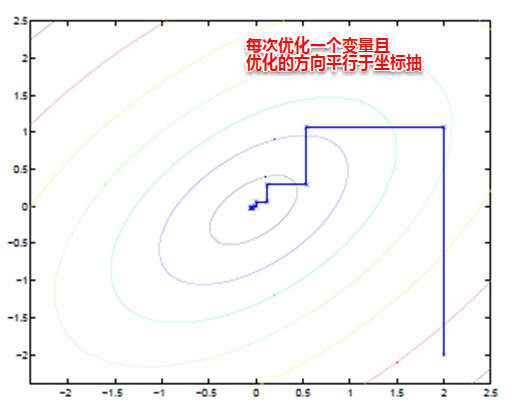
EM算法也可以看作一种“坐标下降法”,首先固定一个值,对另外一个值求极值,不断重复直到收敛。
这时候也许大家就有疑问,问什么不直接这两个家伙求偏导用梯度下降呢?这时候就是坐标下降的优势,有些特殊的函数无法直接求导,这时如果先固定其中的一个变量,再对另一个变量求极值,则变得可行。
4.3 EM算法流程
两枚硬币A和B,假定随机抛掷后正面朝上概率分别为PA,PB。为了估计这两个硬币朝上的概率,咱们轮流抛硬币A和B,每一轮都连续抛5次,总共5轮:
| 硬币 | 结果 | 统计 |
|---|---|---|
| A | 正正反正反 | 3正-2反 |
| B | 反反正正反 | 2正-3反 |
| A | 正反反反反 | 1正-4反 |
| B | 正反反正正 | 3正-2反 |
| A | 反正正反反 | 2正-3反 |
硬币A被抛了15次,在第一轮、第三轮、第五轮分别出现了3次正、1次正、2次正,所以很容易估计出PA,类似的,PB也很容易计算出来(真实值),如下:
PA = (3+1+2)/ 15 = 0.4
PB= (2+3)/10 = 0.5
问题来了,如果我们不知道抛的硬币是A还是B呢(即硬币种类是隐变量),然后再轮流抛五轮,得到如下结果:
| 硬币 | 结果 | 统计 |
|---|---|---|
| Unknown | 正正反正反 | 3正-2反 |
| Unknown | 反反正正反 | 2正-3反 |
| Unknown | 正反反反反 | 1正-4反 |
| Unknown | 正反反正正 | 3正-2反 |
| Unknown | 反正正反反 | 2正-3反 |
OK,问题变得有意思了。现在我们的目标没变,还是估计PA和PB,需要怎么做呢?
显然,此时我们多了一个硬币种类的隐变量,设为z,可以把它认为是一个5维的向量(z1,z2,z3,z4,z5),代表每次投掷时所使用的硬币,比如z1,就代表第一轮投掷时使用的硬币是A还是B。
- 但是,这个变量z不知道,就无法去估计PA和PB,所以,我们必须先估计出z,然后才能进一步估计PA和PB。
- 可要估计z,我们又得知道PA和PB,这样我们才能用极大似然概率法则去估计z,这不是鸡生蛋和蛋生鸡的问题吗,如何破?
答案就是先随机初始化一个PA和PB,用它来估计z,然后基于z,还是按照最大似然概率法则去估计新的PA和PB,然后依次循环,如果新估计出来的PA和PB和我们真实值差别很大,直到PA和PB收敛到真实值为止。
我们不妨这样,先随便给PA和PB赋一个值,比如:
硬币A正面朝上的概率PA = 0.2
硬币B正面朝上的概率PB = 0.7
然后,我们看看第一轮抛掷最可能是哪个硬币。
如果是硬币A,得出3正2反的概率为
0.2
?
0.2
?
0.2
?
0.8
?
0.8
=
0.00512
0.2*0.2*0.2*0.8*0.8 = 0.00512
0.2?0.2?0.2?0.8?0.8=0.00512
如果是硬币B,得出3正2反的概率为
0.7
?
0.7
?
0.7
?
0.3
?
0.3
=
0.03087
0.7*0.7*0.7*0.3*0.3=0.03087
0.7?0.7?0.7?0.3?0.3=0.03087
然后依次求出其他4轮中的相应概率。做成表格如下:
| 轮数 | 若是硬币A | 若是硬币B |
|---|---|---|
| 1 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 2 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
| 3 | 0.08192,即0.2 0.8 0.8 0.8 0.8,1正-4反 | 0.00567,1正-4反 |
| 4 | 0.00512,即0.2 0.2 0.2 0.8 0.8,3正-2反 | 0.03087,3正-2反 |
| 5 | 0.02048,即0.2 0.2 0.8 0.8 0.8,2正-3反 | 0.01323,2正-3反 |
按照最大似然法则:
第1轮中最有可能的是硬币B
第2轮中最有可能的是硬币A
第3轮中最有可能的是硬币A
第4轮中最有可能的是硬币B
第5轮中最有可能的是硬币A
我们就把概率更大,即更可能是A的,即第2轮、第3轮、第5轮出现正的次数2、1、2相加,除以A被抛的总次数15(A抛了三轮,每轮5次),作为z的估计值,B的计算方法类似。然后我们便可以按照最大似然概率法则来估计新的PA和PB。
PA = (2+1+2)/15 = 0.33
PB =(3+3)/10 = 0.6
就这样,不断迭代 不断接近真实值,这就是EM算法的奇妙之处。
可以期待,我们继续按照上面的思路,用估计出的PA和PB再来估计z,再用z来估计新的PA和PB,反复迭代下去,就可以最终得到PA = 0.4,PB=0.5,此时无论怎样迭代,PA和PB的值都会保持0.4和0.5不变,于是乎,我们就找到了PA和PB的最大似然估计。
