前置知识
如果大家对偏导数,方向导数与梯度的概念不是很清楚,欢迎考古:为什么梯度方向是函数增加最快的方向.
实现过程
梯度下降法也叫做梯度下山法,充分补充了前置知识后,然后在理解梯度下降法,会很简单。梯度是所有偏导数组成的Vector,一个点梯度的方向是函数在这个点增加速度最快的方向(具体证明方法在上面已经展示)。
公式如下:
F
(
θ
1
,
θ
2
)
F(\theta_1,\theta_2)
F(θ1?,θ2?)
θ
1
t
e
m
p
=
θ
1
?
a
?
f
?
θ
1
F
(
θ
1
,
θ
2
)
\theta_{1temp}=\theta_1 -a\frac{\partial f}{\partial \theta_1}F(\theta_1,\theta_2)
θ1temp?=θ1??a?θ1??f?F(θ1?,θ2?)
θ
2
t
e
m
p
=
θ
2
?
a
?
f
?
θ
2
F
(
θ
1
,
θ
2
)
\theta_{2temp}=\theta_2 -a\frac{\partial f}{\partial \theta_2}F(\theta_1,\theta_2)
θ2temp?=θ2??a?θ2??f?F(θ1?,θ2?)其中a代表学习率,也就是步长。他代表更新参数时候的步幅迈多大。
重复以上操作,知道
θ
1
,
θ
2
\theta_1,\theta_2
θ1?,θ2?不再变化,这里我们要注意,这两个参数是同时更新,如果先更第一个参数,再用含有第一个更新的参数的函数去更新参数,最后的结果会与梯度下降法有偏差。
我面我们用一个简单地用梯度下降法来优化函数
F
(
θ
1
,
θ
2
)
=
θ
1
2
?
θ
2
2
F(\theta_1,\theta_2)=\theta_1^2-\theta_2^2
F(θ1?,θ2?)=θ12??θ22?在(6,-6)点地参数,来证明梯度下降法。我们可以看出当参数在(0,0)的时候为最小值。
假设a=0.5
θ
1
=
θ
1
?
α
?
f
?
θ
1
f
(
x
,
y
)
=
6
?
0
?
1
×
12
=
4.8
\theta _{1}=\theta _{1}-\alpha \dfrac{\partial f}{\partial \theta _{1}}f\left( x,y\right) =6-0\cdot 1\times 12=4.8
θ1?=θ1??α?θ1??f?f(x,y)=6?0?1×12=4.8
θ
2
=
θ
2
?
α
?
f
?
θ
1
f
(
x
,
y
)
=
?
6
?
(
0
?
1
×
(
?
12
)
)
=
?
4
?
8
\theta _{2}=\theta _{2}-\alpha \dfrac{\partial f}{\partial \theta _{1}}f\left( x,y\right) =-6-\left( 0\cdot 1\times (-12\right) )=-4\cdot 8
θ2?=θ2??α?θ1??f?f(x,y)=?6?(0?1×(?12))=?4?8
我们发现,经过了一次优化,
θ
1
,
θ
2
\theta_1,\theta_2
θ1?,θ2?原点又接近了一步,这样一直往复下去,参数最终就可以达到原点(假设函数为凸函数)。
对一个维度的点求偏导数,如果结果为正,则在这点的这一维度为增函数,反之,则相反,我们知道了增减性,我们就知道了,函数往哪个方向走可以让函数的值达到最小。
沿着梯度减小的方向走,梯度会越来越小,我们步长就会越来越小,到达极值点后,梯度达到水平,梯度值接近0,更新的参数也就不再变化。
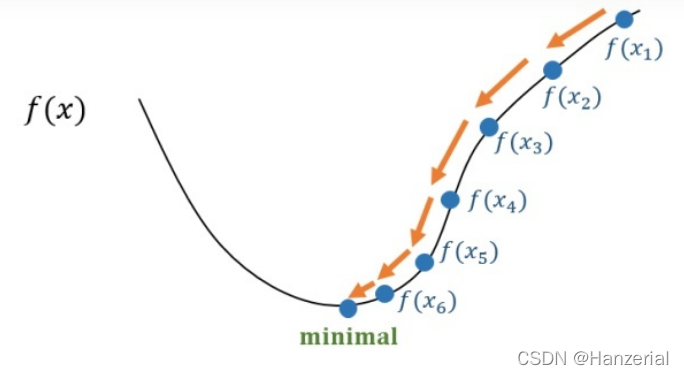
局限性
学习率
对学习率的选择比较苛刻,不能太大不能太小,如果太大,更新参数的时候可能会直接跳过极值点,导致变大,越来越大,最后导致梯度爆炸。
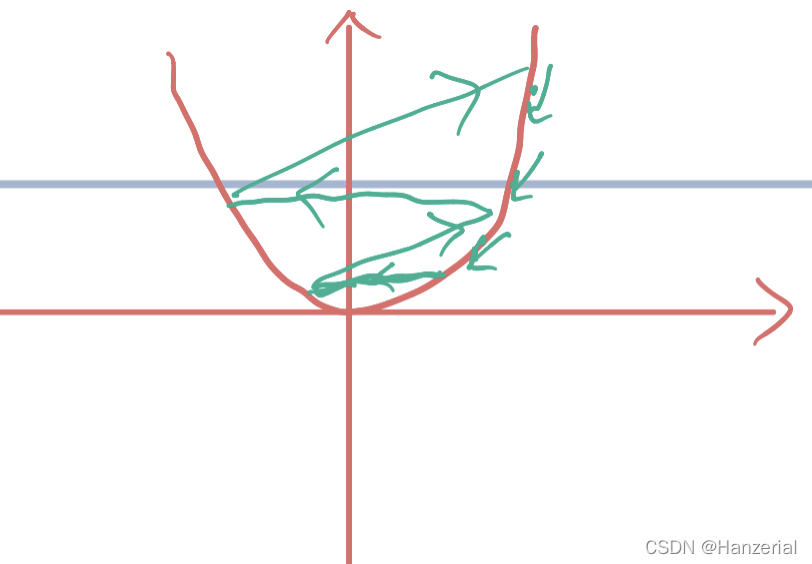
如果学习率太小,会导致学习速度过慢。
在做梯度下降法之前需要对函数进行归一化操作,如果不进行归一化操作,函数找到极值的时间可大大增加,如图所示: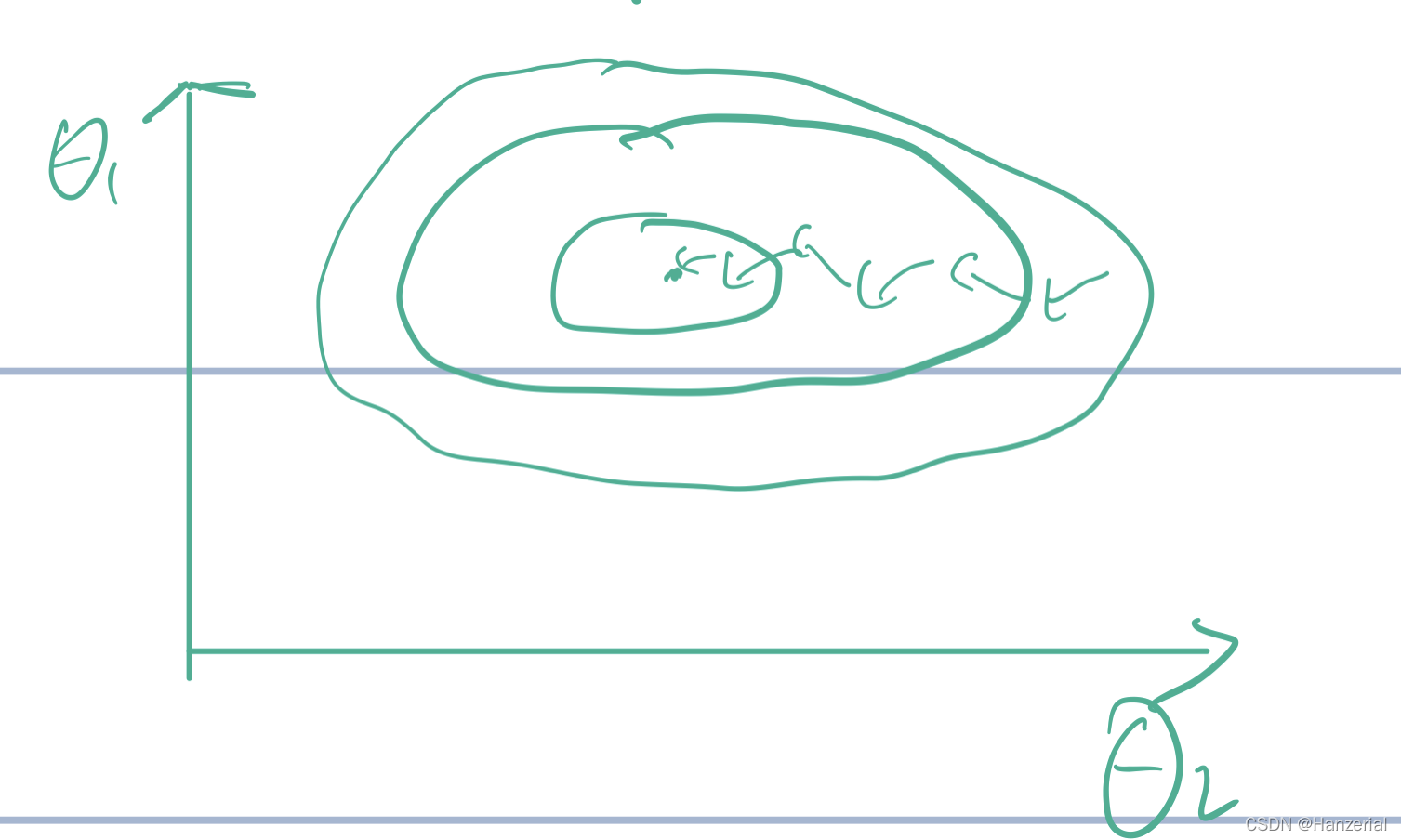
当参数的范围差距不大,等高线图像会更接近于一个圆形,找最优解的需要的时间会大大减少。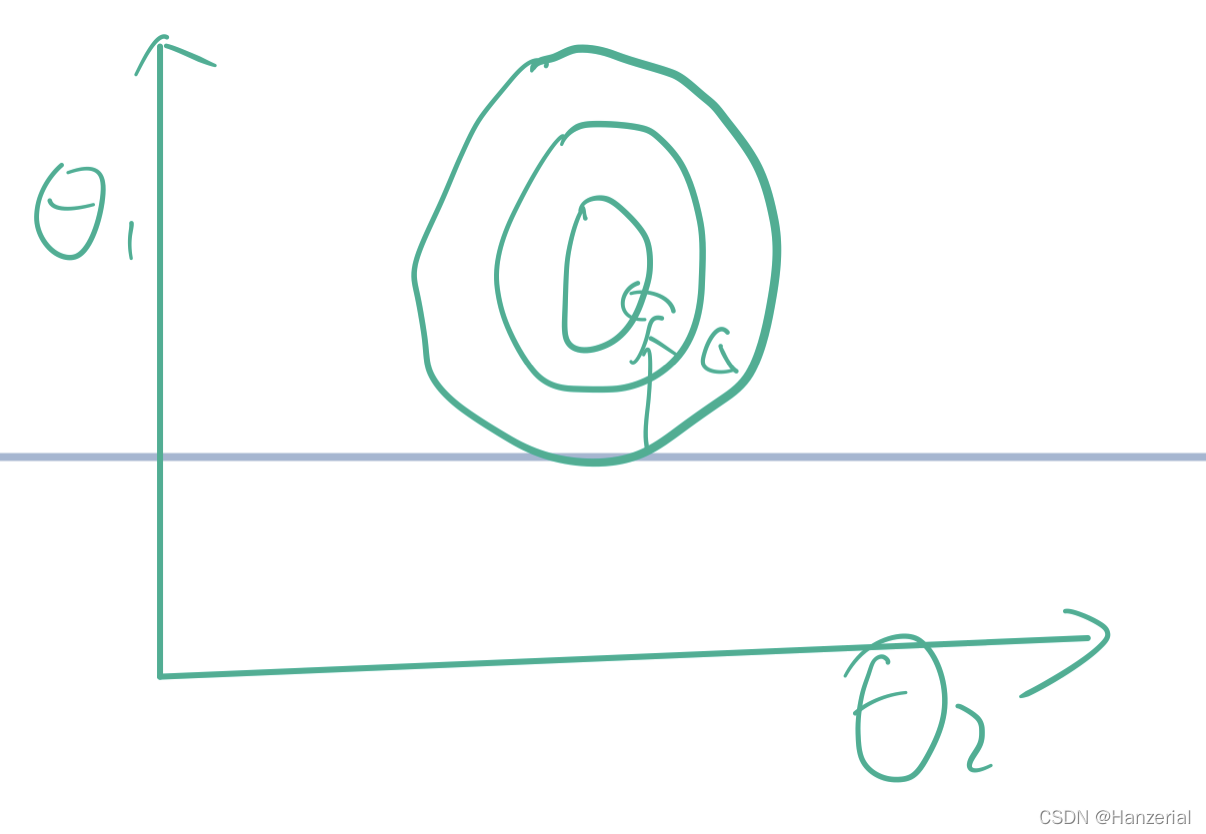
起始点
对起始点值得选择又尤为重要,如果代价函数是一个(非凸函数),那么他的极值点就不唯一,最后的迭代结果可能会是函数得局部最优解。