1,先看运行效果
第一部分
x = torch.tensor([2., 1.], requires_grad=True).view(1,2)
print(x)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)
print(y.shape)
z = torch.mm(x, y)
print(f"z:{z}")
print('*****************')
grad_tensor = torch.Tensor([[1,0]])
print(z.shape)
print(grad_tensor.shape)
print('*****************')
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")结果:
tensor([[2., 1.]], grad_fn=<ViewBackward0>)
torch.Size([2, 2])
z:tensor([[5., 8.]], grad_fn=<MmBackward0>)
*****************
torch.Size([1, 2])
torch.Size([1, 2])
*****************
x.grad: None
y.grad: tensor([[2., 0.],
[1., 0.]])第二部分:
x = torch.tensor([[2., 1.]], requires_grad=True)
print(x)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)
print(y.shape)
z = torch.mm(x, y)
print(f"z:{z}")
print('*****************')
grad_tensor = torch.Tensor([[1,0]])
print(z.shape)
print(grad_tensor.shape)
print('*****************')
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")结果:
tensor([[2., 1.]], requires_grad=True)
torch.Size([2, 2])
z:tensor([[5., 8.]], grad_fn=<MmBackward0>)
*****************
torch.Size([1, 2])
torch.Size([1, 2])
*****************
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],
[1., 0.]])第三部分:
x = torch.tensor([2., 1.]).view(1,2)
x.requires_grad = True
print(x)
y = torch.tensor([[1., 2.], [3., 4.]], requires_grad=True)
print(y.shape)
z = torch.mm(x, y)
print(f"z:{z}")
print('*****************')
grad_tensor = torch.Tensor([[1,0]])
print(z.shape)
print(grad_tensor.shape)
print('*****************')
z.backward(torch.Tensor([[1., 0]]), retain_graph=True)
print(f"x.grad: {x.grad}")
print(f"y.grad: {y.grad}")?结果:
tensor([[2., 1.]], requires_grad=True)
torch.Size([2, 2])
z:tensor([[5., 8.]], grad_fn=<MmBackward0>)
*****************
torch.Size([1, 2])
torch.Size([1, 2])
*****************
x.grad: tensor([[1., 3.]])
y.grad: tensor([[2., 0.],
[1., 0.]])以上是我参考了一篇博客。不过那篇博客有错误,我在他下面进行了评论,推导过程如下:
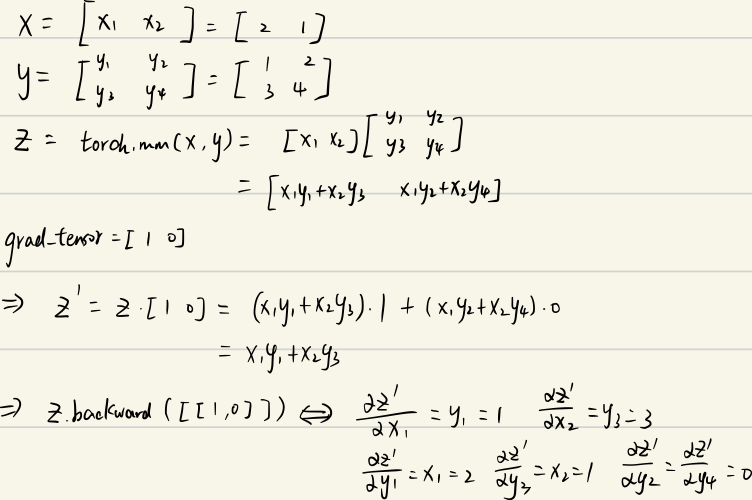
参考博客链接:?Pytorch autograd,backward详解 - marsggbo - 博客园
2,源码分析探本因
"""
``torch.autograd`` provides classes and functions implementing automatic
differentiation of arbitrary scalar valued functions. It requires minimal
changes to the existing code - you only need to declare :class:`Tensor` s
for which gradients should be computed with the ``requires_grad=True`` keyword.
As of now, we only support autograd for floating point :class:`Tensor` types (
half, float, double and bfloat16) and complex :class:`Tensor` types (cfloat, cdouble).
"""
import torch
import warnings
from torch.types import _TensorOrTensors
from typing import Any, Callable, List, Optional, Sequence, Tuple, Union
from .variable import Variable
from .function import Function, NestedIOFunction
from .gradcheck import gradcheck, gradgradcheck
from .grad_mode import no_grad, enable_grad, set_grad_enabled, inference_mode
from .anomaly_mode import detect_anomaly, set_detect_anomaly
from ..overrides import has_torch_function, handle_torch_function
from . import functional
from . import forward_ad
from . import graph
from .. import _vmap_internals
__all__ = ['Variable', 'Function', 'backward', 'grad_mode']
_OptionalTensor = Optional[torch.Tensor]
def _make_grads(outputs: Sequence[torch.Tensor], grads: Sequence[_OptionalTensor],
is_grads_batched: bool) -> Tuple[_OptionalTensor, ...]:
new_grads: List[_OptionalTensor] = []
for out, grad in zip(outputs, grads):
if isinstance(grad, torch.Tensor):
grad_shape = grad.shape if not is_grads_batched else grad.shape[1:]
if not out.shape == grad_shape:
if is_grads_batched:
raise RuntimeError("If `is_grads_batched=True`, we interpret the first "
"dimension of each grad_output as the batch dimension. "
"The sizes of the remaining dimensions are expected to match "
"the shape of corresponding output, but a mismatch "
"was detected: grad_output["
+ str(grads.index(grad)) + "] has a shape of "
+ str(grad.shape) + " and output["
+ str(outputs.index(out)) + "] has a shape of "
+ str(out.shape) + ". "
"If you only want some tensors in `grad_output` to be considered "
"batched, consider using vmap.")
else:
raise RuntimeError("Mismatch in shape: grad_output["
+ str(grads.index(grad)) + "] has a shape of "
+ str(grad.shape) + " and output["
+ str(outputs.index(out)) + "] has a shape of "
+ str(out.shape) + ".")
if out.dtype.is_complex != grad.dtype.is_complex:
raise RuntimeError("For complex Tensors, both grad_output and output"
" are required to have the same dtype."
" Mismatch in dtype: grad_output["
+ str(grads.index(grad)) + "] has a dtype of "
+ str(grad.dtype) + " and output["
+ str(outputs.index(out)) + "] has a dtype of "
+ str(out.dtype) + ".")
new_grads.append(grad)
elif grad is None:
if out.requires_grad:
if out.numel() != 1:
raise RuntimeError("grad can be implicitly created only for scalar outputs")
new_grads.append(torch.ones_like(out, memory_format=torch.preserve_format))
else:
new_grads.append(None)
else:
raise TypeError("gradients can be either Tensors or None, but got " +
type(grad).__name__)
return tuple(new_grads)
def _tensor_or_tensors_to_tuple(tensors: Optional[_TensorOrTensors], length: int) -> Tuple[_OptionalTensor, ...]:
if tensors is None:
return (None, ) * length
if isinstance(tensors, torch.Tensor):
return (tensors, )
return tuple(tensors)
[docs]def backward(
tensors: _TensorOrTensors,
grad_tensors: Optional[_TensorOrTensors] = None,
retain_graph: Optional[bool] = None,
create_graph: bool = False,
grad_variables: Optional[_TensorOrTensors] = None,
inputs: Optional[_TensorOrTensors] = None,
) -> None:
r"""Computes the sum of gradients of given tensors with respect to graph
leaves.
The graph is differentiated using the chain rule. If any of ``tensors``
are non-scalar (i.e. their data has more than one element) and require
gradient, then the Jacobian-vector product would be computed, in this
case the function additionally requires specifying ``grad_tensors``.
It should be a sequence of matching length, that contains the "vector"
in the Jacobian-vector product, usually the gradient of the differentiated
function w.r.t. corresponding tensors (``None`` is an acceptable value for
all tensors that don't need gradient tensors).
This function accumulates gradients in the leaves - you might need to zero
``.grad`` attributes or set them to ``None`` before calling it.
See :ref:`Default gradient layouts<default-grad-layouts>`
for details on the memory layout of accumulated gradients.
.. note::
Using this method with ``create_graph=True`` will create a reference cycle
between the parameter and its gradient which can cause a memory leak.
We recommend using ``autograd.grad`` when creating the graph to avoid this.
If you have to use this function, make sure to reset the ``.grad`` fields of your
parameters to ``None`` after use to break the cycle and avoid the leak.
.. note::
If you run any forward ops, create ``grad_tensors``, and/or call ``backward``
in a user-specified CUDA stream context, see
:ref:`Stream semantics of backward passes<bwd-cuda-stream-semantics>`.
.. note::
When ``inputs`` are provided and a given input is not a leaf,
the current implementation will call its grad_fn (even though it is not strictly needed to get this gradients).
It is an implementation detail on which the user should not rely.
See https://github.com/pytorch/pytorch/pull/60521#issuecomment-867061780 for more details.
Args:
tensors (Sequence[Tensor] or Tensor): Tensors of which the derivative will be
computed.
grad_tensors (Sequence[Tensor or None] or Tensor, optional): The "vector" in
the Jacobian-vector product, usually gradients w.r.t. each element of
corresponding tensors. None values can be specified for scalar Tensors or
ones that don't require grad. If a None value would be acceptable for all
grad_tensors, then this argument is optional.
retain_graph (bool, optional): If ``False``, the graph used to compute the grad
will be freed. Note that in nearly all cases setting this option to ``True``
is not needed and often can be worked around in a much more efficient
way. Defaults to the value of ``create_graph``.
create_graph (bool, optional): If ``True``, graph of the derivative will
be constructed, allowing to compute higher order derivative products.
Defaults to ``False``.
inputs (Sequence[Tensor] or Tensor, optional): Inputs w.r.t. which the gradient
be will accumulated into ``.grad``. All other Tensors will be ignored. If
not provided, the gradient is accumulated into all the leaf Tensors that
were used to compute the attr::tensors.
"""
if grad_variables is not None:
warnings.warn("'grad_variables' is deprecated. Use 'grad_tensors' instead.")
if grad_tensors is None:
grad_tensors = grad_variables
else:
raise RuntimeError("'grad_tensors' and 'grad_variables' (deprecated) "
"arguments both passed to backward(). Please only "
"use 'grad_tensors'.")
if inputs is not None and len(inputs) == 0:
raise RuntimeError("'inputs' argument to backward() cannot be empty.")
tensors = (tensors,) if isinstance(tensors, torch.Tensor) else tuple(tensors)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else \
tuple(inputs) if inputs is not None else tuple()
grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors))
grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
if retain_graph is None:
retain_graph = create_graph
# The reason we repeat same the comment below is that
# some Python versions print out the first line of a multi-line function
# calls in the traceback and some print out the last line
Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
tensors, grad_tensors_, retain_graph, create_graph, inputs,
allow_unreachable=True, accumulate_grad=True) # Calls into the C++ engine to run the backward pass
[docs]def grad(
outputs: _TensorOrTensors,
inputs: _TensorOrTensors,
grad_outputs: Optional[_TensorOrTensors] = None,
retain_graph: Optional[bool] = None,
create_graph: bool = False,
only_inputs: bool = True,
allow_unused: bool = False,
is_grads_batched: bool = False
) -> Tuple[torch.Tensor, ...]:
r"""Computes and returns the sum of gradients of outputs with respect to
the inputs.
``grad_outputs`` should be a sequence of length matching ``output``
containing the "vector" in vector-Jacobian product, usually the pre-computed
gradients w.r.t. each of the outputs. If an output doesn't require_grad,
then the gradient can be ``None``).
.. note::
If you run any forward ops, create ``grad_outputs``, and/or call ``grad``
in a user-specified CUDA stream context, see
:ref:`Stream semantics of backward passes<bwd-cuda-stream-semantics>`.
.. note::
``only_inputs`` argument is deprecated and is ignored now (defaults to ``True``).
To accumulate gradient for other parts of the graph, please use
``torch.autograd.backward``.
Args:
outputs (sequence of Tensor): outputs of the differentiated function.
inputs (sequence of Tensor): Inputs w.r.t. which the gradient will be
returned (and not accumulated into ``.grad``).
grad_outputs (sequence of Tensor): The "vector" in the vector-Jacobian product.
Usually gradients w.r.t. each output. None values can be specified for scalar
Tensors or ones that don't require grad. If a None value would be acceptable
for all grad_tensors, then this argument is optional. Default: None.
retain_graph (bool, optional): If ``False``, the graph used to compute the grad
will be freed. Note that in nearly all cases setting this option to ``True``
is not needed and often can be worked around in a much more efficient
way. Defaults to the value of ``create_graph``.
create_graph (bool, optional): If ``True``, graph of the derivative will
be constructed, allowing to compute higher order derivative products.
Default: ``False``.
allow_unused (bool, optional): If ``False``, specifying inputs that were not
used when computing outputs (and therefore their grad is always zero)
is an error. Defaults to ``False``.
is_grads_batched (bool, optional): If ``True``, the first dimension of each
tensor in ``grad_outputs`` will be interpreted as the batch dimension.
Instead of computing a single vector-Jacobian product, we compute a
batch of vector-Jacobian products for each "vector" in the batch.
We use the vmap prototype feature as the backend to vectorize calls
to the autograd engine so that this computation can be performed in a
single call. This should lead to performance improvements when compared
to manually looping and performing backward multiple times. Note that
due to this feature being experimental, there may be performance
cliffs. Please use ``torch._C._debug_only_display_vmap_fallback_warnings(True)``
to show any performance warnings and file an issue on github if warnings exist
for your use case. Defaults to ``False``.
"""
outputs = (outputs,) if isinstance(outputs, torch.Tensor) else tuple(outputs)
inputs = (inputs,) if isinstance(inputs, torch.Tensor) else tuple(inputs)
overridable_args = outputs + inputs
if has_torch_function(overridable_args):
return handle_torch_function(
grad,
overridable_args,
outputs,
inputs,
grad_outputs=grad_outputs,
retain_graph=retain_graph,
create_graph=create_graph,
only_inputs=only_inputs,
allow_unused=allow_unused,
)
if not only_inputs:
warnings.warn("only_inputs argument is deprecated and is ignored now "
"(defaults to True). To accumulate gradient for other "
"parts of the graph, please use torch.autograd.backward.")
grad_outputs_ = _tensor_or_tensors_to_tuple(grad_outputs, len(outputs))
grad_outputs_ = _make_grads(outputs, grad_outputs_, is_grads_batched=is_grads_batched)
if retain_graph is None:
retain_graph = create_graph
# The reason we repeat same the comment several times below is because
# some Python versions print out the first line of multi-line function
# calls in the traceback and some print out the last line
if is_grads_batched:
def vjp(gO):
return Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
outputs, gO, retain_graph, create_graph, inputs,
allow_unused, accumulate_grad=False) # Calls into the C++ engine to run the backward pass
return _vmap_internals._vmap(vjp, 0, 0, allow_none_pass_through=True)(grad_outputs)
else:
return Variable._execution_engine.run_backward( # Calls into the C++ engine to run the backward pass
outputs, grad_outputs_, retain_graph, create_graph, inputs,
allow_unused, accumulate_grad=False) # Calls into the C++ engine to run the backward pass
# This function applies in case of gradient checkpointing for memory
# optimization. Currently, gradient checkpointing is supported only if the
# execution engine is invoked through torch.autograd.backward() and its
# inputs argument is not passed. It is not supported for torch.autograd.grad().
# This is because if inputs are specified, the gradient won't be calculated for
# anything else e.g. model parameters like weights, bias etc.
#
# This function returns whether the checkpointing is valid i.e. torch.autograd.backward
# or not i.e. torch.autograd.grad. The implementation works by maintaining a thread
# local variable in torch/csrc/autograd/engine.cpp which looks at the NodeTask
# in the stack and before a NodeTask is executed in evaluate_function, it
# checks for whether reentrant backwards is imperative or not.
# See https://github.com/pytorch/pytorch/pull/4594 for more discussion/context
def _is_checkpoint_valid():
return Variable._execution_engine.is_checkpoint_valid()
def variable(*args, **kwargs):
warnings.warn("torch.autograd.variable(...) is deprecated, use torch.tensor(...) instead")
return torch.tensor(*args, **kwargs)
if not torch._C._autograd_init():
raise RuntimeError("autograd initialization failed")
# Import all native method/classes
from torch._C._autograd import (DeviceType, ProfilerActivity, ProfilerState, ProfilerConfig, ProfilerEvent,
_enable_profiler_legacy, _disable_profiler_legacy, _profiler_enabled,
_enable_record_function, _set_empty_test_observer, kineto_available,
_record_function_with_args_enter, _record_function_with_args_exit,
_supported_activities, _add_metadata_json, SavedTensor,
_push_saved_tensors_default_hooks, _pop_saved_tensors_default_hooks)
from torch._C._autograd import (_ProfilerResult, _KinetoEvent,
_prepare_profiler, _enable_profiler, _disable_profiler)
from . import profiler
def _register_py_tensor_class_for_device(device, cls):
if not isinstance(cls, type):
raise RuntimeError("cls isn't a typeinfo object")
torch._C._register_py_class_for_device(device, cls)Tensor.backward调用Tensor.autograd.backward,后续我们所说的backward都是指后者哈。
在backward中重要的参数是
grad_tensors_ = _tensor_or_tensors_to_tuple(grad_tensors, len(tensors))
grad_tensors_ = _make_grads(tensors, grad_tensors_, is_grads_batched=False)
?其中grad_tensors就是指我们上述代码示例中的torch.Tensor([[1,0]])
调用backward之后会调用一个_make_grads()的函数,这个函数看着挺唬人,其实函数体里面大部分都是判断grad_tensors和tensor的关系,比如shape等,就是相当于检测你求梯度的时候是标量还是别的什么。
在backward函数中有说明
The graph is differentiated using the chain rule. If any of ``tensors`` are non-scalar (i.e. their data has more than one element) and require gradient, then the Jacobian-vector product would be computed, in this case the function additionally requires specifying ``grad_tensors``. It should be a sequence of matching length, that contains the "vector" in the Jacobian-vector product, usually the gradient of the differentiated function w.r.t. corresponding tensors (``None`` is an acceptable value for all tensors that don't need gradient tensors).
翻译过来就是:
使用链规则对图形进行区分。如果任何“张量”
? ? 是非标量的(即它们的数据具有多个元素),并且需要
? ? 梯度,然后计算雅可比向量积,如下所示
? ? 函数还需要指定“grad_tensors”。
? ? 它应该是一个匹配长度的序列,其中包含“向量”
? ? 在雅可比向量积中,通常是微分的梯度
? ? 函数 w.r.t. 相应的张量(“无”是
? ? 所有不需要梯度张量的张量)。
?意思是如果是非标量,需要一个雅克比向量。
未完待续
