视觉机器学习20讲-MATLAB源码示例(17)-RBM学习算法
1. RBM学习算法
受限玻尔兹曼机(restricted Boltzmann machine, RBM)是一种可通过输入数据集,学习概率分布的随机生成型神经网络。RBM最初由Paul Smolensky 于1986年提出,并将该模型命名为Harmonium(簧风琴),后又由Geoffrey Hinton 教授改进发明了快速的训练算法才被广泛使用,并由此得名RBM。RBM主要可用于降维、分类、协同过滤、表征学习及神经网络预训练等场景。
受限玻尔兹曼机因该模型是玻尔兹曼机的简化版而得名。玻尔兹曼机是一种随机神经网络,得名于其使用到的分布为统计力学中的玻尔兹曼分布。受限玻尔兹曼机相对于玻尔兹曼机,其简化了网络中同层之间的相连条件,即不存在层内各节点的相互连接。这样,网络中同层的各节点之间就相互独立。
2. Matlab仿真
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
%功能:演示RBM学习算法在计算机视觉中的应用
%RBM学习过程;
%环境:Win7,Matlab2018a
%Modi: C.S
%时间:2022-04-05
%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%%
function RBMLearning()
%% load training and testing data
clear;
data = load('../data/mnist.mat');
train_x = double(data.train_x) / 255;
clear('data');
%% train RBM model using train_x
% set RBM parameters
num_epochs = 10;
batch_size = 100;
input_dim = size(train_x, 2);
hidden_sz = 100;
rbm.alpha = 1;
rbm.momentum = 0.1;
rbm.W = zeros(hidden_sz, input_dim);
rbm.vW = zeros(hidden_sz, input_dim);
rbm.b = zeros(input_dim, 1);
rbm.vb = zeros(input_dim, 1);
rbm.c = zeros(hidden_sz, 1);
rbm.vc = zeros(hidden_sz, 1);
% train RBM using CD
disp('Start to train RBM:');
rng(0);
m = size(train_x, 1);
num_batches = floor(m / batch_size);
for i = 1 : num_epochs
kk = randperm(m);
err = 0;
for j = 1 : num_batches
batch = train_x(kk((j-1)*batch_size+1:j*batch_size),:);
v1 = batch;
h1 = sigmrnd(repmat(rbm.c', batch_size, 1) + v1 * rbm.W');
v2 = sigmrnd(repmat(rbm.b', batch_size, 1) + h1 * rbm.W );
h2 = sigm(repmat(rbm.c', batch_size, 1) + v2 * rbm.W');
c1 = h1' * v1;
c2 = h2' * v2;
rbm.vW = rbm.momentum * rbm.vW + rbm.alpha * (c1 - c2) / batch_size;
rbm.vb = rbm.momentum * rbm.vb + rbm.alpha * sum(v1 - v2)' / batch_size;
rbm.vc = rbm.momentum * rbm.vc + rbm.alpha * sum(h1 - h2)' / batch_size;
rbm.W = rbm.W + rbm.vW;
rbm.b = rbm.b + rbm.vb;
rbm.c = rbm.c + rbm.vc;
err = err + sum(sum((v1 - v2).^ 2)) / batch_size;
end
disp(['RBM train: epoch ' num2str(i) '/' num2str(num_epochs) '. Average reconstruction error is: ' num2str(err / num_batches)]);
end
%% visualize the trained model
V = rbm.W';
minmax = [min(V(:)), max(V(:))];
sz = sqrt(input_dim);
s1 = sz;
s2 = sz;
num=ceil(sqrt(hidden_sz));
data=minmax(2)*ones(num*s2+num-1,num*s1+num-1);
x=0;
y=0;
for i=1:hidden_sz
im = reshape(V(:,i),s1,s2)';
data(x*s2+1+x : x*s2+s2+x, y*s1+1+y : y*s1+s1+y)=im;
x=x+1;
if(x>=num)
x=0;
y=y+1;
end
end
imagesc(data, [minmax(1) minmax(2)]);
axis equal
axis tight
colormap gray
end
%% other helper functions
function X = sigm(P)
X = 1./(1+exp(-P));
end
function X = sigmrnd(P)
X = double(1./(1+exp(-P)) > rand(size(P)));
end
3. 仿真结果
>> RBMLearning
Start to train RBM:
RBM train: epoch 1/10. Average reconstruction error is: 65.5958
RBM train: epoch 2/10. Average reconstruction error is: 49.8328
RBM train: epoch 3/10. Average reconstruction error is: 46.2584
RBM train: epoch 4/10. Average reconstruction error is: 44.5693
RBM train: epoch 5/10. Average reconstruction error is: 43.5177
RBM train: epoch 6/10. Average reconstruction error is: 42.6902
RBM train: epoch 7/10. Average reconstruction error is: 42.2639
RBM train: epoch 8/10. Average reconstruction error is: 41.8363
RBM train: epoch 9/10. Average reconstruction error is: 41.5267
RBM train: epoch 10/10. Average reconstruction error is: 41.2922
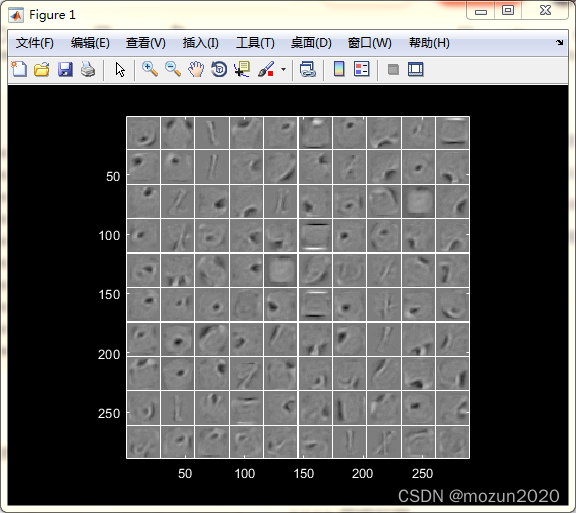
4. 小结
受限玻尔兹曼机可以看做是一种基于能量的概率图模型,我们建立了数据分布与能量函数之间的关系,通过能量函数来描绘RBM可视层与隐藏层神经元之间的联合概率分布。
RBM的训练问题根本上就是一个最大似然估计,但其中联合概率分布项的配分函数难以计算。Hinton教授提出了用CD-k算法来有效降低Gibbs采样的次数,进而近似计算梯度,从而使RBM能运用到实际中。
RBM与一般多层前馈感知机不同,其值可双向传播,拥有与多层前馈感知机不同的更新参数方式(back-propagation)。
其他关于RBM参数如何选择,训练时的技巧,请参看Geoffrey Hinton教授的RBM指南。
关于RBM具体详情,有兴趣的推荐去仔细查看全文《机器学习20讲》中第十七讲内容,深入学习了解,MATLAB仿真源码和数据在分享的资源中已打包好,欢迎取用。
