匈牙利算法

匈牙利算法最早是由匈牙利数学家Dénes K?nig康尼格和Jen? Egerváry用来求矩阵中0元素的个数的一种方法。由此他证明『矩阵中独立0元素的最多个数等于能覆盖cover所有0元素的最少直线数』
匈牙利算法是一种在多项式时间内求解任务分配问题的组合优化算法，并推动了后来的原始对偶方法。
1955年，美国数学家哈罗德·库恩W.W.Kuhn（库恩）Harold W. Kuhn在求解著名的指派问题时引用了这一结论，并对具体算法做了改进，仍然称为匈牙利算法。此算法之所以被称作匈牙利算法，是因为算法很大一部分是基于以前匈牙利数学家Dénes K?nig和Jen? Egerváry的工作之上创建起来的。[1][2]
1957年，詹姆士·芒克勒斯Munkres在1957年回顾了该算法，并发现它的时间复杂度为（强）多项式时间。[3] 此后该算法被称为Kuhn–Munkres算法或Munkres分配算法。原始算法的时间复杂度为 $O(n^{4})$ ，但杰克·爱德蒙斯与卡普发现可以修改算法达到 $O(n^{3})$ 运行时间，富泽也独立发现了这一点。L·R·福特和D·R·福尔克森将该方法推广到了一般运输问题。2006年发现卡尔·雅可比?Jacobis bound在19世纪就解决了指派问题，该解法在他死后在1890年以拉丁文发表。[4]

参考书目[编辑]

R.E. Burkard, M. Dell'Amico, S. Martello: Assignment Problems (Revised reprint). SIAM, Philadelphia (PA.) 2012. ISBN 978-1-61197-222-1
M. Fischetti, "Lezioni di Ricerca Operativa", Edizioni Libreria Progetto Padova, Italia, 1995.
R. Ahuja, T. Magnanti, J. Orlin, "Network Flows", Prentice Hall, 1993.
S. Martello, "Jeno Egerváry: from the origins of the Hungarian algorithm to satellite communication". Central European Journal of Operations Research 18, 47–58, 2010

参考文献[编辑]

^ Harold W. Kuhn, "The Hungarian Method for the assignment problem", Naval Research Logistics Quarterly, 2: 83–97, 1955. Kuhn's original publication.
^ Harold W. Kuhn, "Variants of the Hungarian method for assignment problems", Naval Research Logistics Quarterly, 3: 253–258, 1956.
?https://econweb.ucsd.edu/~v2crawford/hungar.pdf??Kuhn的paper1960年9月29日。
^ J. Munkres, "Algorithms for the Assignment and Transportation Problems", Journal of the Society for Industrial and Applied Mathematics, 5(1):32–38, 1957 March.
^ JACOBI'S BOUND

外部链接[编辑]

Bruff, Derek, "The Assignment Problem and the Hungarian Method", [1] （页面存档备份，存于互联网档案馆）
Mordecai J. Golin, Bipartite Matching and the Hungarian Method, Course Notes, Hong Kong University of Science and Technology.
R. A. Pilgrim, Munkres' Assignment Algorithm. Modified for Rectangular Matrices （页面存档备份，存于互联网档案馆）, Course notes, Murray State University.
Mike Dawes, The Optimal Assignment Problem, Course notes, University of Western Ontario.
On Kuhn's Hungarian Method – A tribute from Hungary, András Frank, Egervary Research Group, Pazmany P. setany 1/C, H1117, Budapest, Hungary.
Lecture: Fundamentals of Operations Research - Assignment Problem - Hungarian Algorithm, Prof. G. Srinivasan, Department of Management Studies, IIT Madras.
Extension: Assignment sensitivity analysis (with O(n^4) time complexity), Liu, Shell.
Solve any Assignment Problem online, provides a step by step explanation of the Hungarian Algorithm.

实现[编辑]

（请注意，并非所有这些都满足 $O(n^{3})$ 时间约束。）?

?二、Matlab版本的匈牙利Hungarian算法

Matlab实现一：?https://www.mathworks.com/matlabcentral/fileexchange/6543-functions-for-the-rectangular-assignment-problem?
Matlab实现二：C:\Users\XXXX\Documents\MATLAB\Examples\vision\MotionBasedMultiObjectTrackingExample 中的? ? ? ? [assignments, unassignedTracks, unassignedDetections] =?assignDetectionsToTracks(cost, costOfNonAssignment); 函数就调用了匈牙利算法。
matlab exchange 上面关于匈牙利算法的所有实现：https://www.mathworks.com/matlabcentral/fileexchange?q=Hungarian+algorithm

?使用第二个实现方法来分析匈牙利算法的过程，核心代码如下：

James Munkres' variant of the Hungarian?assignment algorithm.?

?References:

Matt L. Miller, Harold S. Stone, and Ingemar J. Cox. Optimizing Murty's?Ranked Assignment Method. ?IEEE Transactions on Aerospace and??Electronic Systems, 33(3), 1997
James Munkres, Algorithms for Assignment and Transportation Problems,?Journal of the Society for Industrial and Applied Mathematics Volume 5,?Number 1, March, 1957
R. A. Pilgrim. Munkres' Assignment Algorithm Modified for Rectangular?Matrices http://csclab.murraystate.edu/bob.pilgrim/445/munkres.html?

[assignments, unassignedTracks, unassignedDetections] =?assignDetectionsToTracks(costMatrix, costOfNonAssignment)

costMatrix 是一个 M×N 矩阵，其中 M 是轨道数，N 是检测数。
costMatrix(i,j) 是将第 j 个检测分配给第 i 个轨道的成本。成本越低，分配的可能性就越大。
costOfNonAssignment 是一个标量，它表示未分配的轨道或检测remain unassigned仍然未被分配的成本。costOfNonAssignment 值越大，表明每个现有轨道都会以较高的可能性将被分配一个检测。
输出：assignments 是一个 L×2 的索引对轨道和相应的检测矩阵，其中 L 是对的数量。第一列包含轨道索引，第二列包含相应的检测索引。 unassignedTracks 是 P 元素，其中 P 是未分配轨道的数量。每个元素是未分配检测的轨道的索引。未分配检测是 Q 元素向量，其中 Q 是未分配检测的数量。每个元素是未分配给任何轨道的检测索引。这些检测可以开始新的轨道。?

..assignDetectionsToTracks(costMatrix,unassignedTrackCost,..unassignedDetectionCost) 分别指定未分配轨迹和检测的cost。

输入：unassignedTrackCost 是标量或 M 元素向量，其中 M 是轨迹数。对于 M 元素向量，每个元素表示不给每个track分配任何检测的cost。标量输入表示未分配所有轨道的相同成本。成本可能会因您对每个轨道和场景的了解而异。例如，如果物体即将离开视野，相应轨迹的未分配的代价应该很低。
unassignedDetectionCost是标量或N元素向量，其中N是检测次数。对于N元素向量，每个元素表示为该检测启动新轨道的cost。标量输入表示未分配所有轨道的相同成本。成本可能会因您对每个检测和场景的了解而有所不同。例如，如果检测图像出现在靠近图像边缘的位置，它更有可能是一个新物体。

关闭科学计数法：?MATLAB关闭科学计数法显示_Ray-Soft的博客-CSDN博客_matlab取消科学计数法

小数位个数变少：?format short e

function [matches, unassignedTracks, unassignedDetections] = ...
    assignDetectionsToTracks(costMatrix, costUnassignedTracks, ...
    costUnassignedDetections)

%#codegen
%#ok<*EMCLS>
%#ok<*EMCA>

% Parse and check inputs
checkCost(costMatrix);
checkUnassignedCost(costUnassignedTracks, 'costUnassignedTracks');

coder.internal.errorIf(nargin == 2 && ~isscalar(costUnassignedTracks), ...
    'vision:assignDetectionsToTracks:costOfNotMatchingMustBeScalar');
coder.internal.errorIf(~isa(costMatrix, class(costUnassignedTracks)), ...
    'vision:assignDetectionsToTracks:allInputsMustBeSameClass');
if nargin > 2
    checkUnassignedCost(costUnassignedDetections, ...
        'costUnassignedDetections');
    coder.internal.errorIf(~isa(costMatrix, class(costUnassignedDetections)), ...
        'vision:assignDetectionsToTracks:allInputsMustBeSameClass');
    coder.internal.errorIf(~isscalar(costUnassignedTracks) && ...
        (numel(costUnassignedTracks) ~= size(costMatrix, 1)), ...
        'vision:assignDetectionsToTracks:costUnmatchedTracksInvalidSize');
    coder.internal.errorIf(~isscalar(costUnassignedDetections) && ...
        (numel(costUnassignedDetections) ~= size(costMatrix, 2)), ...
        'vision:assignDetectionsToTracks:costUnmatchedDetectionsInvalidSize');
end
 
theClass = class(costMatrix);
costUnmatchedTracksVector = ones(1, size(costMatrix, 1), theClass) .* ...
    costUnassignedTracks;
if nargin > 2    
    costUnmatchedDetectionsVector = ones(1, size(costMatrix, 2), theClass) ...
            .* costUnassignedDetections;
else    
    costUnmatchedDetectionsVector = ones(1, size(costMatrix, 2), theClass) .*...
        costUnassignedTracks;        
end

[matches, unassignedTracks, unassignedDetections] = ...
    cvalgAssignDetectionsToTracks(costMatrix, costUnmatchedTracksVector, ...
    costUnmatchedDetectionsVector);

%-------------------------------------------------------------------------
function tf = checkCost(cost)
validateattributes(cost, {'numeric'}, ...
    {'real', 'nonsparse', 'nonnan', '2d'}, ...
    'assignDetectionsToTracks', 'cost');
tf = true;

%-------------------------------------------------------------------------
function tf = checkUnassignedCost(val, varName)
validateattributes(val, {'numeric'}, ...
    {'vector', 'finite', 'real', 'nonsparse'}, ...
    'assignDetectionsToTracks', varName); 
tf = true;

%-------------------------------------------------------------------------
function [matches, unmatchedTracks, unmatchedDetections] = ...
    cvalgAssignDetectionsToTracks(cost, costUnmatchedTracks, ...
    costUnmatchedDetections)

% add dummy rows and columns to account for the possibility of 
% unassigned tracks and observations
paddedCost = getPaddedCost(cost, costUnmatchedTracks, ...
    costUnmatchedDetections);

% solve the assignment problem
[rowInds, colInds] = find(hungarianAssignment(paddedCost));

rows = size(cost, 1);
cols = size(cost, 2);
unmatchedTracks = uint32(rowInds(rowInds <= rows & colInds > cols));
unmatchedDetections = uint32(colInds(colInds <= cols & rowInds > rows));

matches = uint32([rowInds, colInds]);
matches = matches(rowInds <= rows & colInds <= cols, :);
if isempty(matches)
    matches = zeros(0, 2, 'uint32');
end

%-------------------------------------------------------------------------
function paddedCost = getPaddedCost(cost, costUnmatchedTracks,...
    costUnmatchedDetections)
% replace infinities with the biggest possible number
bigNumber = getTheHighestPossibleCost(cost);
cost(isinf(cost)) = bigNumber;

% create a "padded" cost matrix, with dummy rows and columns
% to account for the possibility of not matching
rows = size(cost, 1);
cols = size(cost, 2);
paddedSize = rows + cols;
paddedCost = ones(paddedSize, class(cost)) * bigNumber;

paddedCost(1:rows, 1:cols) = cost;

for i = 1:rows
    paddedCost(i, cols+i) = costUnmatchedTracks(i);
end
for i = 1:cols
    paddedCost(rows+i, i) = costUnmatchedDetections(i);
end
paddedCost(rows+1:end, cols+1:end) = 0;

%-------------------------------------------------------------------------
function bigNumber = getTheHighestPossibleCost(cost)
if isinteger(cost)
    bigNumber = intmax(class(cost));
else
    bigNumber = realmax(class(cost));
end

%-------------------------------------------------------------------------
function assignment = hungarianAssignment(cost)

assignment = true(size(cost));
if isempty(cost)
    return;
end
fprintf("原始padding cost=\n")
disp(cost)
% step 1: subtract row minima
cost = bsxfun(@minus, cost, min(cost, [], 2));
fprintf("step1-减去行最小值后: \ncost=\n")
disp(cost)
% step 2: make an initial assignment by "starring" zeros 
stars = makeInitialAssignment(cost);
fprintf("step2-初始猜测 \nstar=\n")
disp(stars)
% step 3: cover all columns containing starred zeros
colCover = any(stars);

while ~all(colCover)
    % uncover all rows and unprime all zeros
    rowCover = false(1, size(cost, 1));
    primes = false(size(stars));
    Z = ~cost; % mark locations of the zeros
    Z(:, colCover) = false;
    while 1
        shouldCreateNewZero = true;
        % step 4: Find a noncovered zero and prime it.
        [zi, zj] = findNonCoveredZero(Z);
        while zi > 0
            primes(zi, zj) = true;
            % find a starred zero in the column containing the primed zero
            starredRow = stars(zi, :);
            if any(starredRow)
                % if there is one, cover the its row and uncover
                % its column.
                rowCover(zi) = true;
                colCover(starredRow) = false;
                Z(zi, :) = false;
                Z(~rowCover, starredRow) = ~cost(~rowCover, starredRow);
                [zi, zj] = findNonCoveredZero(Z);
            else
                shouldCreateNewZero = false;
                % go to step 5
                break;
            end
        end
        
        if shouldCreateNewZero
            % step 6: create a new zero
            [cost, Z] = createNewZero(cost, rowCover, colCover);
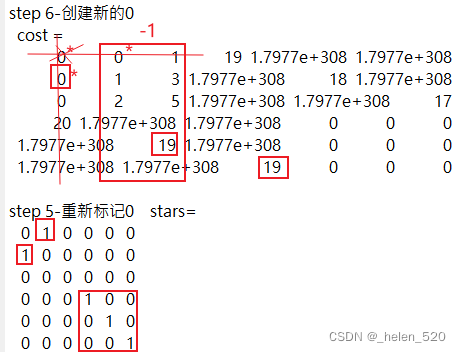
            fprintf("step 6-创建新的0\n  cost = \n")
            disp(cost)
        else
            break;
        end
    end
    
    % step 5: Construct a series of alternating primed and starred zeros.
    stars = alternatePrimesAndStars(stars, primes, zi, zj);
    fprintf("step 5-重新标记0    stars=\n")
    disp(stars)
    % step 3: cover all columns containing starred zeros
    colCover = any(stars);
end
assignment = stars;

%-------------------------------------------------------------------------
function stars = makeInitialAssignment(cost)
rowCover = false(1, size(cost, 1));
colCover = false(1, size(cost, 2));
stars = false(size(cost));

[zr, zc] = find(cost == 0);
for i = 1:numel(zr)
    if ~rowCover(zr(i)) && ~colCover(zc(i))
        stars(zr(i), zc(i)) = true;
        rowCover(zr(i)) = true;
        colCover(zc(i)) = true;
    end
end

%-------------------------------------------------------------------------
function [zi, zj] = findNonCoveredZero(Z)
fprintf("step 4- 查找Z是否有0\nZ=\n")
disp(Z)
[i, j] = find(Z, 1);
if isempty(i)
    zi = -1;
    zj = -1;
else
    zi = i(1);
    zj = j(1);
end

%-------------------------------------------------------------------------
function [cost, Z] = createNewZero(cost, rowCover, colCover)
Z = false(size(cost));

% find a minimum uncovered value
uncovered = cost(~rowCover, ~colCover);
minVal = min(uncovered(:));

% add the minimum value to all intersections of covered rows and cols
cost(rowCover, colCover) = cost(rowCover, colCover) + minVal;
    
% subtract the minimum value from all uncovered entries creating at
% least one new zero
cost(~rowCover, ~colCover) = uncovered - minVal;
    
% mark locations of all uncovered zeros
Z(~rowCover, ~colCover) = ~cost(~rowCover, ~colCover);

%-------------------------------------------------------------------------
% Step 5.
% Construct a series of alternating primed and starred zeros.  
% Start with the primed uncovered zero Z0 at (zi, zj).  Find a starred zero 
% Z1 in the column of Z0. Star Z0, and unstar Z1. Find a primed zero Z2 in 
% the row of Z1. If the are no starred zeros in the column of Z2, stop.  
% Otherwise repeat with Z0 = Z2.
function stars = alternatePrimesAndStars(stars, primes, zi, zj)
nRows = size(stars, 1);
nCols = size(stars, 2);

% create a logical index of Z0
lzi = false(1, nRows);
lzj = false(1, nCols);
lzi(zi) = true;
lzj(zj) = true;

% find a starred zero Z1 in the column of Z0
rowInd = stars(1:nRows, lzj);

% star Z0
stars(lzi, lzj) = true;

while any(rowInd(:))
    % unstar Z1
    stars(rowInd, lzj) = false;
    
    % find a primed zero Z2 in Z1's row
    llzj = primes(rowInd, 1:nCols);
    lzj = llzj(1, :);
    lzi = rowInd;
    
    % find a starred zero in Z2's column
    rowInd = stars(1:nRows, lzj);
    
    % star Z2
    stars(lzi, lzj) = true;
end

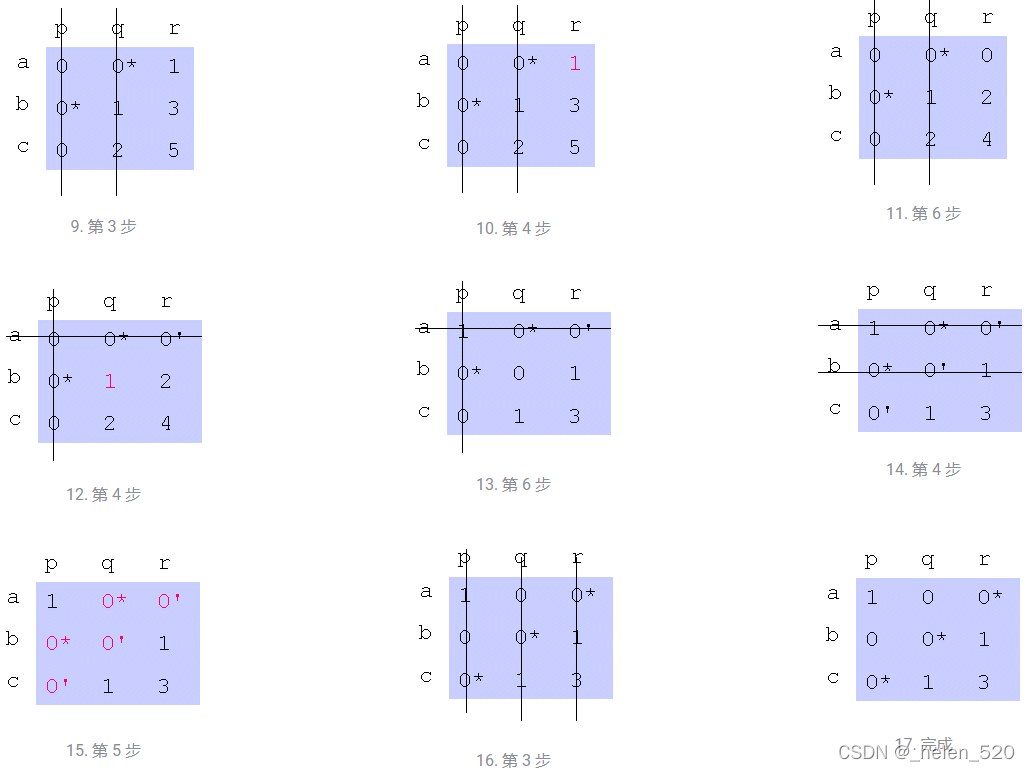
?2.1 分配算法举例说明

例子来源于：The Algorithm Workshop - Bevilacqua Research Corporation

用上面的matlab跑一遍，并输出的中间过程为：

假设cost为：?[1,2,3;2,4,6;3,6,9]

调用方法为：[assignments, unassignedTracks, unassignedDetections] = ...
assignDetectionsToTracks(cost, 20);

?上述代码基本上与下述的过程是一致的。

?2.2 一个匹配有问题的案例。（应该新建一个Track，但是没有）

cost =

? ? ?1 ? ? 2 ? ?30
? ? ?2 ? ? 4 ? ?30
? ? ?3 ? ? 6 ? ?30
step 5-重新标记0 ? ?stars=
? ?0 ? 1 ? 0 ? 0 ? 0 ? 0
? ?1 ? 0 ? 0 ? 0 ? 0 ? 0
? ?0 ? 0 ? 1 ? 0 ? 0 ? 0
? ?0 ? 0 ? 0 ? 1 ? 0 ? 0
? ?0 ? 0 ? 0 ? 0 ? 1 ? 0
? ?0 ? 0 ? 0 ? 0 ? 0 ? 1

还是给第三个检测分配了第三个ID，但是第三个检测是都不匹配的，已经都超出我的距离范畴了。还在匹配，这就出现了问题。

如何fix这个问题？？？