1.贝叶斯分类器属于生成式模型
对于数据的判别分类有两种策略模型:判别式模型和生成式模型
判别式模型
: 逻辑回归、决策树、支持向量机等为常见的判别式模型,这种模型需要人为的设定好模型框架,假如Y=WX+B>1为好瓜,Y=WX+B<=1为坏瓜,然后通过数据的训练,不断地修正模型参数,模型对于目标变量的条件预测也就更加准确。再比如决策树,通过信息熵,信息增益等判断标准,对好瓜具有的属性进行判别选择,通过对数据的学习,得到决策模型。
生成式模型
: 生成方法由数据学习联合概率分布P(Y,X),然后求出条件概率分布P(X|Y)作为预测的模型P(Y|X)。在西瓜书中便是让模型学习好瓜具有什么属性,然后根据这些属性来判断什么是好瓜。
2.贝叶斯定理
贝叶斯公式:

该公式描述的是随机事件A和B在其中某事件发生的情况下发生的概率,其中分子描述的是事件A、B都发生的联合概率,分母描述的是事件A发生的全概率,补充公式如下:


引用百度文库解释贝叶斯定理的例子:
贝叶斯定理在检测吸毒者时很有用。假设一个常规的检测结果的敏感度与可靠度均为99%,也就是说,当被检者吸毒时,每次检测呈阳性(用“Y”表示)的概率为。而被检者不吸毒时,每次检测呈阴性(用“y”表示)的概率为99%。从检测结果的概率来看,检测结果是比较准确的,但是贝叶斯定理却可以揭示一个潜在的问题。假设某公司将对其全体雇员进行一次鸦片吸食情况的检测,已知0.5%的雇员吸毒。我们想知道,每位医学检测呈阳性的雇员吸毒的概率有多高。令“D”为该公司雇员吸毒事件,“N”为该公司雇员不吸毒事件,“Y”为该公司雇员检测呈阳性事件。可得
(1)P(D)代表雇员吸毒的概率,该值为0.5%,这个值为先验概率
(2)P(N)代表雇员不吸毒的概率,该值为99.5%,也就是1-P(D)
(3)P(Y|D)代表吸毒者阳性检出率,这是一个条件概率同时也是先验概率,阳性检测准确性是99%
(4)P(Y|N)代表不吸毒者阳性检出率,也就是出错检测的概率,该值为1%,因为对于不吸毒者,其检测为阴性的概率为99%,因此,其被误检测成阳性的概率为1-99%
(5)P(Y)代表不考虑其他因素的影响的阳性检出率,根据全概率公式可得 P(Y) = P(Y,D) + P(Y,N) = P(Y|D)P(D)+P(Y|N)P(N) =99%*0.5%+1%*99.5% = 0.0149
由上述条件可以得到某人在检测阳性的情况下吸毒的概率:

文式图如下:
3.朴素贝叶斯分类器
3.1朴素贝叶斯分类器中的数学模型

其中P(x)对于所有分类标记均相同,所以P(x)与类标记无关,求P(c|x)就x相当于求P?和P(x|c)
3.2分类器的分类准则
A.求P(x|c),直接根据每个属性估计该条件概率
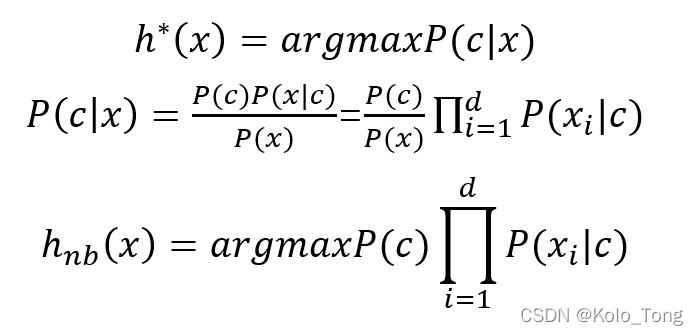
其中的P?表示的是各个样本占全部样本的比例,比如好瓜占全部瓜的比例;P(x|c)表示样本为c的情况下属性为x的比例,比如在好瓜中属性为纹理清晰的瓜所占的比例。
直接根据贝叶斯判断准则h(x)得出的大小判定样本属于哪一类别
B.利用极大似然估计
根据先验知识判断数据可能的数据分布情况,假设一个分布(如正态分布),对训练数据进行参数估计,这种方法的好处是可以利用数据直接进行相关运算便得到数据的概率分布;缺点是该方法严重依赖所假设的分布,如果假设不准则训练结果不佳。
