- 目标函数
- 加法模型
- 基学习器
- 回归树
- 表达式
- 基学习器
- 前向分步算法
- 目标函数推导
- 加法模型
- 构建树的方法
- 系统设计
回归树
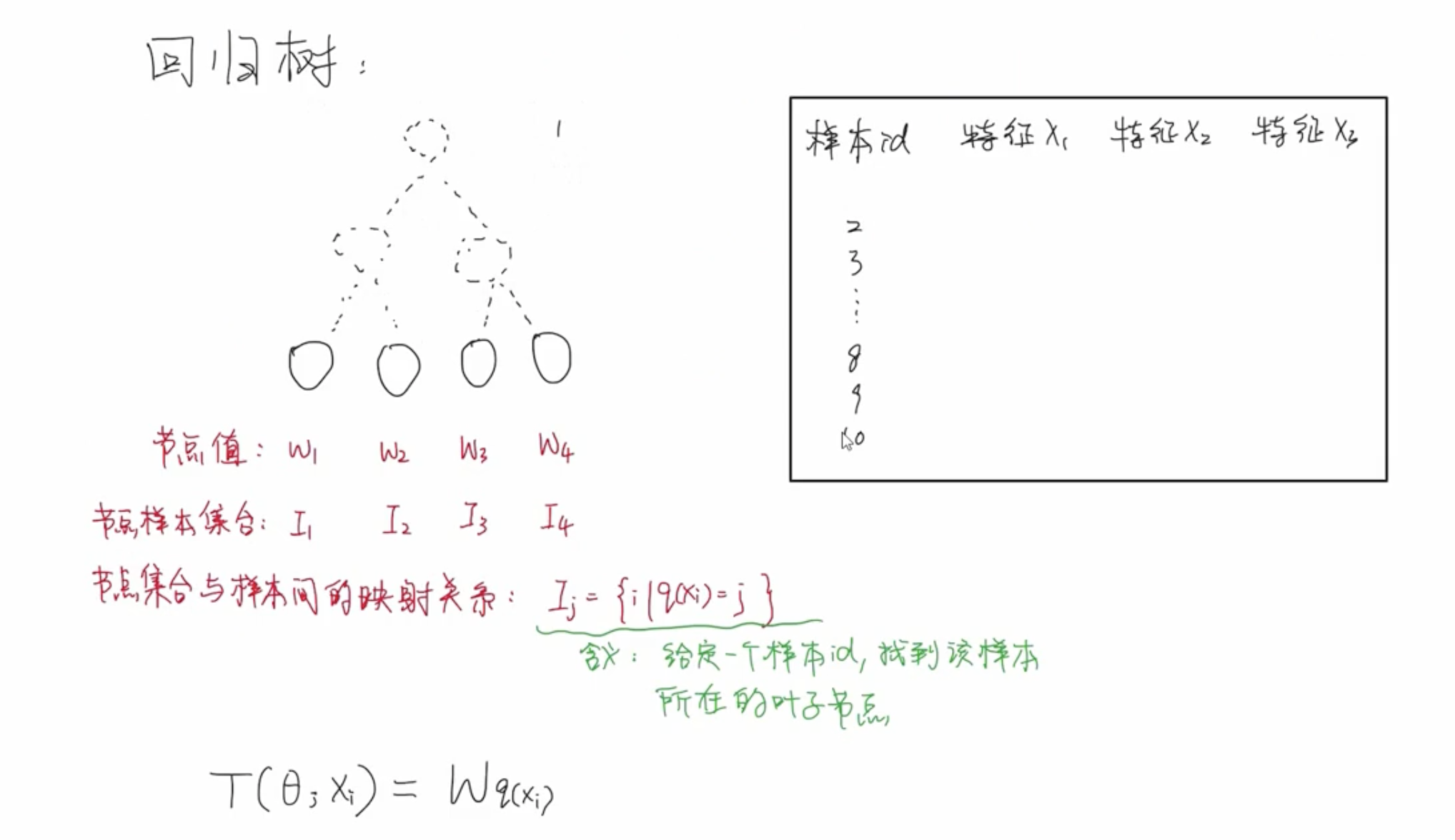
XGBoost 属于加法模型,其中每个基学习器都采用回归树,采用前向分布算法逐步优化其中的每一个基学习器。
按照优化模型的一般步骤,定义好模型之后就需要把目标函数写出来,然后把问题转化成一个求解最优值的问题。比如将损失函数降到最小。然后利用各种求解最优质的方法求解出基学习器中的参数。
模型表达(加法模型)
y i M ^ = ∑ j = 1 M f j ( x i ) = ∑ j = 1 M ? 1 f j ( x i ) + f j ( M ) ( x i ) = y i ( M ? 1 ) ^ + f j ( M ) ( x i ) \hat{y^M_{i}} = \sum^{M}_{j=1}f_j(x_i) = \sum_{j=1}^{M-1}f_j(x_i) + f_j^{(M)}(x_i) = \hat{y_i^{(M-1)}} + f_j^{(M)}(x_i) yiM?^?=j=1∑M?fj?(xi?)=j=1∑M?1?fj?(xi?)+fj(M)?(xi?)=yi(M?1)?^?+fj(M)?(xi?)
前向分布算法
前向分布算法采用贪心的策略逐棵逐棵树进行训练。
y i t ^ = y i ( t ? 1 ) ^ + f t ( x i ) = y i ( t ? 1 ) ^ + W q ( x i ) \hat{y^t_i} = \hat{y^{(t-1)}_i} + f_t(x_i) = \hat{y^{(t-1)}_i} + W_{q(x_i)} yit?^?=yi(t?1)?^?+ft?(xi?)=yi(t?1)?^?+Wq(xi?)?
f t ( x i ) = W q ( x i ) f_t(x_i) = W_{q(x_i)} ft?(xi?)=Wq(xi?)?
目标函数
O b j ( t ) = ∑ i = 1 N L ( y i , y i t ^ ) + ∑ j = 1 t Ω ( f j ) Obj^{(t)} = \sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \sum_{j=1}^{t}\Omega(f_j) Obj(t)=i=1∑N?L(yi?,yit?^?)+j=1∑t?Ω(fj?)
优化目标
( w 1 ? , w 2 ? , . . . , w M ? ) = a r g m i n ?? ∑ i = 1 N L ( y i , y i t ^ ) + ∑ j = 1 t Ω ( f j ) (w_1^*, w_2^*,..., w_M^*) = argmin\;\sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \sum_{j=1}^{t}\Omega(f_j) (w1??,w2??,...,wM??)=argmini=1∑N?L(yi?,yit?^?)+j=1∑t?Ω(fj?)
其中, Ω ( f t ) = γ ?? T + 1 2 λ ∑ j = 1 T W j 2 \Omega(f_t) = \gamma\;T + \frac{1}{2}\lambda\sum_{j=1}^{T}W_j^2 Ω(ft?)=γT+21?λ∑j=1T?Wj2?.
( w 1 ? , w 2 ? , . . . , w M ? ) = a r g m i n ?? ∑ i = 1 N L ( y i , y i t ^ ) + ∑ j = 1 t Ω ( f j ) (w_1^*, w_2^*,..., w_M^*) = argmin\;\sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \sum_{j=1}^{t}\Omega(f_j) (w1??,w2??,...,wM??)=argmini=1∑N?L(yi?,yit?^?)+j=1∑t?Ω(fj?)
= a r g m i n ?? ∑ i = 1 N L ( y i , y i t ^ ) + ∑ j = 1 t ? 1 Ω ( f j ) + Ω ( f t ) = argmin\;{\sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \sum_{j=1}^{t-1}\Omega(f_j) + \Omega(f_t)} =argmini=1∑N?L(yi?,yit?^?)+j=1∑t?1?Ω(fj?)+Ω(ft?)
= a r g m i n ?? ∑ i = 1 N L ( y i , y i t ^ ) + Ω ( f t ) = argmin\;{\sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \Omega(f_t)} =argmini=1∑N?L(yi?,yit?^?)+Ω(ft?)
其中, ∑ j = 1 t ? 1 Ω ( f j ) \sum_{j=1}^{t-1}\Omega(f_j) ∑j=1t?1?Ω(fj?) 是前 t-1 棵树的正则项,在 t 时刻为已经求得的常量值,因此在 argmin 过程中可以省略该部分。
树模型不适合使用梯度下降法迭代优化,因为树模型都是阶跃的不连续的。
( w 1 ? , w 2 ? , . . . , w M ? ) = a r g m i n ?? ∑ i = 1 N L ( y i , y i t ^ ) + Ω ( f j ) (w_1^*, w_2^*,..., w_M^*) = argmin\;\sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) +\Omega(f_j) (w1??,w2??,...,wM??)=argmini=1∑N?L(yi?,yit?^?)+Ω(fj?)
= ∑ i = 1 N L ( y i , y i t ^ ) + γ ?? T + 1 2 λ ∑ j = 1 T W j 2 = \sum_{i=1}^{N}L(y_i, \hat{y^{t}_i}) + \gamma\;T + \frac{1}{2}\lambda\sum_{j=1}^{T}W_j^2 =i=1∑N?L(yi?,yit?^?)+γT+21?λj=1∑T?Wj2?
= ∑ j = 1 T ∑ i ∈ I j L ( y i , y i ( t ) ^ ) + γ ?? T + 1 2 λ ∑ j = 1 T W j 2 = \sum_{j=1}^{T}\sum_{i \in I_j}L(y_i, \hat{y^{(t)}_{i}}) + \gamma\;T + \frac{1}{2}\lambda\sum_{j=1}^{T}W_j^2 =j=1∑T?i∈Ij?∑?L(yi?,yi(t)?^?)+γT+21?λj=1∑T?Wj2?
= γ ?? T + ∑ j = 1 T [ ∑ i ∈ I j [ L ( y i , y i ( t ) ^ ) ] + 1 2 λ ?? W j 2 ] = \gamma\;T + \sum_{j=1}^{T}[\sum_{i \in I_j}[L(y_i, \hat{y^{(t)}_{i}})]+\frac{1}{2}\lambda\;W_j^2] =γT+j=1∑T?[i∈Ij?∑?[L(yi?,yi(t)?^?)]+21?λWj2?]
其中, y i ( t ) ^ = y i ( t ? 1 ) ^ + W q ( x i ) = y i ( t ? 1 ) ^ + W j \hat{y^{(t)}_i} = \hat{y^{(t-1)}_i} + W_{q(x_i)} = \hat{y^{(t-1)}_i} + W_{j} yi(t)?^?=yi(t?1)?^?+Wq(xi?)?=yi(t?1)?^?+Wj?。所以,
= γ ?? T + ∑ j = 1 T [ ∑ i ∈ I j [ L ( y i , y i ( t ? 1 ) ^ + W j ) ] + 1 2 λ ?? W j 2 ] = \gamma\;T + \sum_{j=1}^{T}[\sum_{i \in I_j}[L(y_i, \hat{y^{(t-1)}_{i}} + W_j)]+\frac{1}{2}\lambda\;W_j^2] =γT+j=1∑T?[i∈Ij?∑?[L(yi?,yi(t?1)?^?+Wj?)]+21?λWj2?]
泰勒二阶展开式: f ( x ) ≈ f ( x 0 ) + f ′ ( x 0 ) ( x ? x 0 ) + 1 2 f ′ ′ ( x 0 ) ( x ? x 0 ) 2 f(x) \approx f(x_0) + f'(x_0)(x-x_0) + \frac{1}{2}f''(x_0)(x-x_0)^2 f(x)≈f(x0?)+f′(x0?)(x?x0?)+21?f′′(x0?)(x?x0?)2
= L ( y i , y i ( t ? 1 ) ^ + W j ) ≈ L ( y i , y i ( t ? 1 ) ^ ) + L ′ ( y i , y i ( t ? 1 ) ^ ) W j + 1 2 L ′ ′ ( y i , y i ( t ? 1 ) ^ ) W j 2 = L(y_i, \hat{y^{(t-1)}_i}+W_j) \approx L(y_i, \hat{y^{(t-1)}_i}) + L'(y_i, \hat{y^{(t-1)}_i})W_j + \frac{1}{2}L''(y_i, \hat{y^{(t-1)}_i})W_j^{2} =L(yi?,yi(t?1)?^?+Wj?)≈L(yi?,yi(t?1)?^?)+L′(yi?,yi(t?1)?^?)Wj?+21?L′′(yi?,yi(t?1)?^?)Wj2?
其中,记 L ′ ( y i , y i ( t ? 1 ) ^ ) L'(y_i, \hat{y^{(t-1)}_i}) L′(yi?,yi(t?1)?^?) 为 g i g_i gi?,记 L ′ ′ ( y i , y i ( t ? 1 ) ^ ) L''(y_i, \hat{y^{(t-1)}_i}) L′′(yi?,yi(t?1)?^?) 为 h i h_i hi?。
L ( y i , y i ( t ? 1 ) ^ + W j ) ≈ L ( y i , y i ( t ? 1 ) ^ ) + g i ?? W j + 1 2 h i ?? W j 2 L(y_i, \hat{y^{(t-1)}_i}+W_j) \approx L(y_i, \hat{y^{(t-1)}_i}) + g_i\;W_j + \frac{1}{2}h_i\;W_j^2 L(yi?,yi(t?1)?^?+Wj?)≈L(yi?,yi(t?1)?^?)+gi?Wj?+21?hi?Wj2?
整理,可的目标函数为:
O b j ( t ) = γ ?? T + ∑ j = 1 T [ ∑ i ∈ I j [ L ( y i , y i ( t ) ^ ) ] + 1 2 λ ?? W j 2 ] Obj^{(t)} = \gamma\;T + \sum_{j=1}^{T}[\sum_{i \in I_j}[L(y_i, \hat{y^{(t)}_{i}})]+\frac{1}{2}\lambda\;W_j^2] Obj(t)=γT+j=1∑T?[i∈Ij?∑?[L(yi?,yi(t)?^?)]+21?λWj2?]
= γ ?? T + ∑ j = 1 T [ ∑ i ?? ∈ ?? I j ( g i ?? W j + 1 2 h i W j 2 ) + 1 2 λ ?? W j 2 ] = \gamma\;T + \sum_{j=1}^{T}[\sum_{i\;\in\;I_j}(g_i\;W_j + \frac{1}{2}h_iW_j^2) + \frac{1}{2}\lambda\;W_j^2] =γT+j=1∑T?[i∈Ij?∑?(gi?Wj?+21?hi?Wj2?)+21?λWj2?]
= γ ?? T + ∑ j = 1 T [ W j ∑ i ∈ I j g i + 1 2 W j 2 ∑ i ∈ I j h i + 1 2 λ W j 2 ] = \gamma\;T + \sum_{j=1}^T[W_j\sum_{i\in I_j}g_i + \frac{1}{2}W_j^2\sum_{i\in I_j}h_i + \frac{1}{2}\lambda W_j^2] =γT+j=1∑T?[Wj?i∈Ij?∑?gi?+21?Wj2?i∈Ij?∑?hi?+21?λWj2?]
= γ ?? T + ∑ j = 1 T [ W j ∑ i ∈ I j g i + 1 2 W j 2 ( λ + ∑ i ∈ I j h i ) ] = \gamma\;T + \sum_{j=1}^T[W_j\sum_{i\in I_j}g_i + \frac{1}{2}W_j^2(\lambda + \sum_{i\in I_j}h_i)] =γT+j=1∑T?[Wj?i∈Ij?∑?gi?+21?Wj2?(λ+i∈Ij?∑?hi?)]
其中,记 ∑ i ∈ I j g i \sum_{i \in I_j}g_i ∑i∈Ij??gi? 为 G j G_j Gj?,记 ∑ i ∈ I j h i \sum_{i \in I_j}h_i ∑i∈Ij??hi? 为 H j H_j Hj?。 g i g_i gi? 表示一阶梯度, h i h_i hi? 表示二阶梯度,这两者都是可以直接求解得出来的。 G j G_j Gj? 表示树模型中 j j j 号叶子结点中所有样本的一阶梯度和, H j H_j Hj? 表示树模型中 j j j 号叶子结点中所有样本的二阶梯度和。
O b j ( t ) = γ ?? T + ∑ j = 1 T [ W j ?? G j + 1 2 W j 2 ( λ + H j ) ] Obj^{(t)}= \gamma\;T + \sum_{j=1}^T[W_j\;G_j + \frac{1}{2}W_j^2(\lambda + H_j)] Obj(t)=γT+j=1∑T?[Wj?Gj?+21?Wj2?(λ+Hj?)]
| 样本id | 特征 x 1 x_1 x1? | 特征 x 2 x_2 x2? | y | y ^ = W j \hat{y}=W_j y^?=Wj? | L ( y , y ^ ) L(y,\hat{y}) L(y,y^?) | g i g_i gi? | h i h_i hi? |
|---|---|---|---|---|---|---|---|
| 1 | y 1 y_1 y1? | W 1 W_1 W1? | L 1 L_1 L1? | g 1 g_1 g1? | h 1 h_1 h1? | ||
| 2 | y 2 y_2 y2? | W 2 W_2 W2? | L 2 L_2 L2? | g 2 g_2 g2? | h 2 h_2 h2? | ||
| 3 | y 3 y_3 y3? | W 3 W_3 W3? | L 3 L_3 L3? | g 3 g_3 g3? | h 3 h_3 h3? | ||
| 4 | y 4 y_4 y4? | W 4 W_4 W4? | L 4 L_4 L4? | g 4 g_4 g4? | h 4 h_4 h4? | ||
| 5 | y 5 y_5 y5? | W 5 W_5 W5? | L 5 L_5 L5? | g 5 g_5 g5? | h 5 h_5 h5? | ||
W 1 ? = a r g m i n ?? ( W 1 G 1 + 1 2 W 1 2 ( λ + H 1 ) ) W_1^* = argmin\;(W_1G_1 + \frac{1}{2}W_1^2(\lambda + H_1)) W1??=argmin(W1?G1?+21?W12?(λ+H1?))
W 2 ? = a r g m i n ?? ( W 2 G 2 + 1 2 W 2 2 ( λ + H 2 ) ) W_2^* = argmin\;(W_2G_2 + \frac{1}{2}W_2^2(\lambda + H_2)) W2??=argmin(W2?G2?+21?W22?(λ+H2?))
W 3 ? = a r g m i n ?? ( W 3 G 3 + 1 2 W 3 2 ( λ + H 3 ) ) W_3^* = argmin\;(W_3G_3 + \frac{1}{2}W_3^2(\lambda + H_3)) W3??=argmin(W3?G3?+21?W32?(λ+H3?))
W 4 ? = a r g m i n ?? ( W 4 G 4 + 1 2 W 4 2 ( λ + H 4 ) ) W_4^* = argmin\;(W_4G_4 + \frac{1}{2}W_4^2(\lambda + H_4)) W4??=argmin(W4?G4?+21?W42?(λ+H4?))
W 5 ? = a r g m i n ?? ( W 5 G 5 + 1 2 W 5 2 ( λ + H 5 ) ) W_5^* = argmin\;(W_5G_5 + \frac{1}{2}W_5^2(\lambda + H_5)) W5??=argmin(W5?G5?+21?W52?(λ+H5?))
其中, 当每个叶子结点中的样本确定后,就可以计算出 G j G_j Gj? 和 H j H_j Hj? 的具体值。
W j ? = ? b 2 a = ? G j H j + λ W_j^* = -\frac{b}{2a} = - \frac{G_j}{H_j + \lambda} Wj??=?2ab?=?Hj?+λGj??
O b j ( t ) ? = m i n ?? O b j ( t ) ≈ γ ?? T ? 1 2 ∑ j = 1 T G j 2 H j + λ {Obj^{(t)}}^{*} = min\;Obj^{(t)} \approx \gamma\;T - \frac{1}{2}\sum_{j=1}^{T}\frac{G_j^2}{H_j + \lambda} Obj(t)?=minObj(t)≈γT?21?j=1∑T?Hj?+λGj2??
每当我们拿到一个数据集的时候,可以直接计算出一阶梯度 g i g_i gi? 和二阶梯度 h i h_i hi? 的数值,每个叶子结点中的所有样本一阶梯度加和得到 G j G_j Gj?,所有样本的二阶梯度加和得到 H j H_j Hj?。然后就可以根据公式计算出节点的 W j ? W_j^* Wj?? 的值,同时可以计算出最小的损失 O b j ( t ) ? {Obj^{(t)}}^* Obj(t)? 的值。
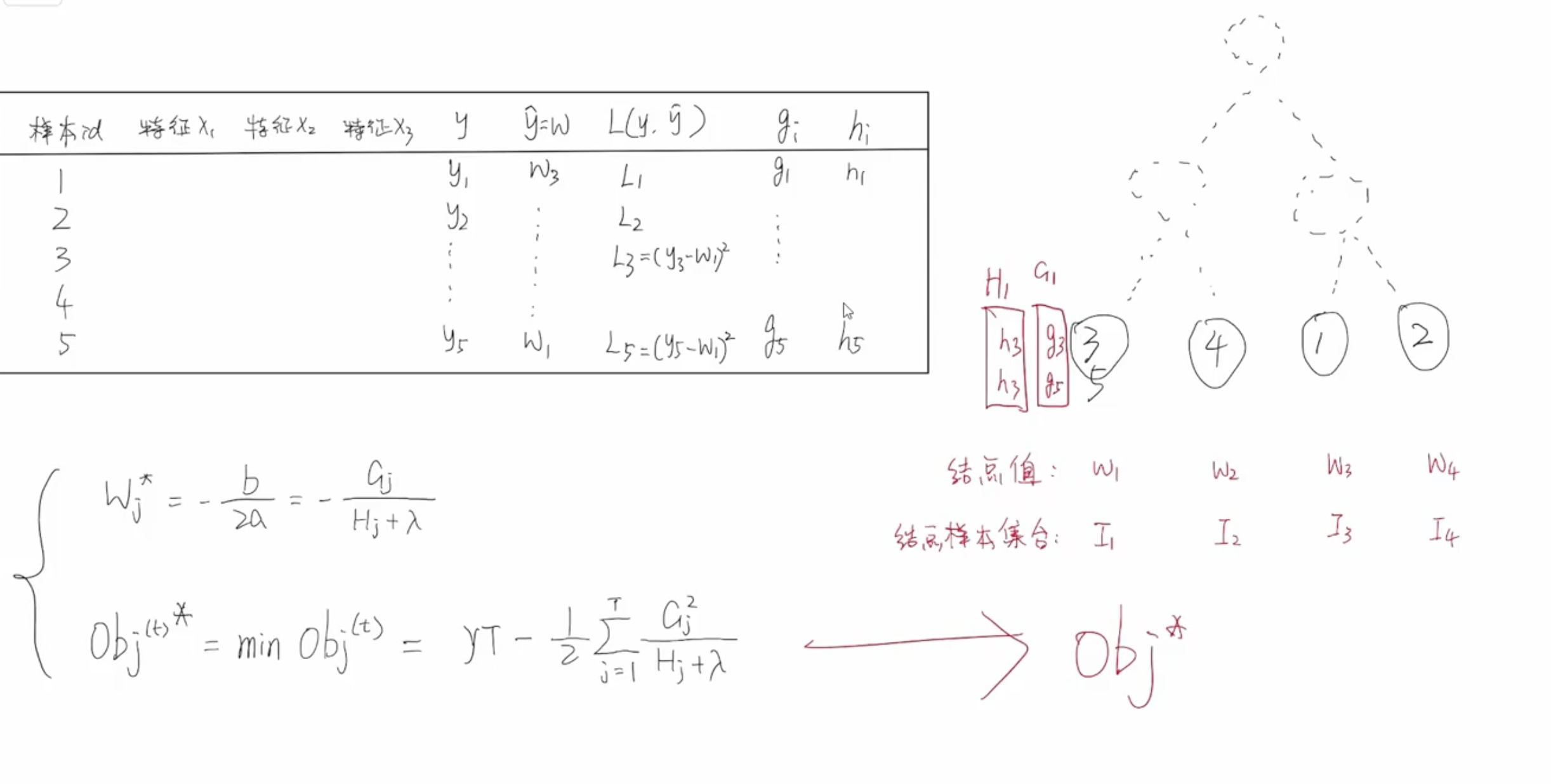
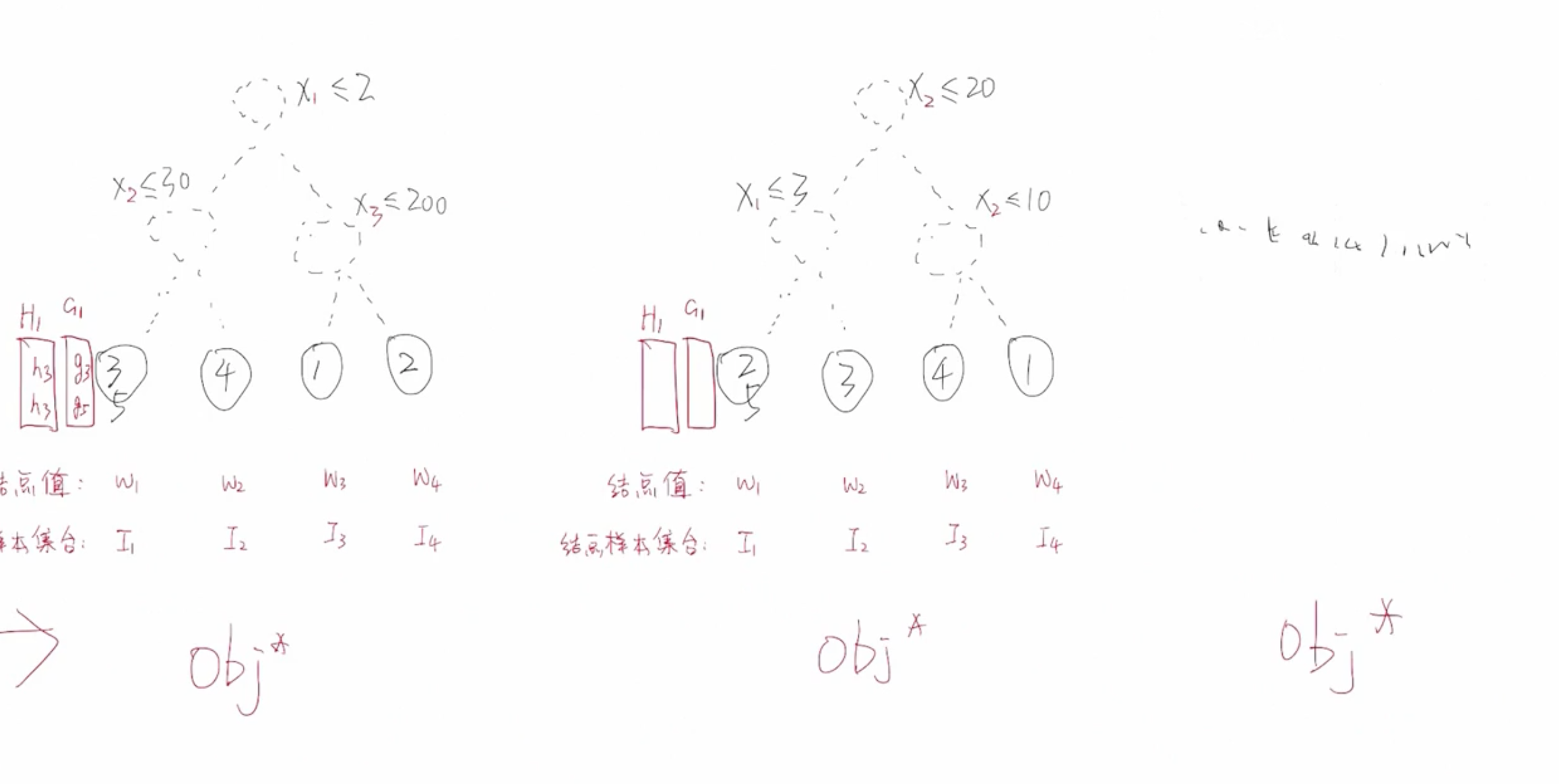
当划分调节不一样的时候,树结构不同,意味着同样的一批样本输入到树中最终落入叶子节点的分布就会不同,计算出来的 G j , ?? H j , ?? W j ? , ?? O b j ( t ) ? G_j,\;H_j,\;W_j^*,\;{Obj^{(t)}}^* Gj?,Hj?,Wj??,Obj(t)? 的这些值就会不一样。那么我们该如何选择最优的树呢?
根据不同的划分条件可以生成不同的树,每棵树都可以计算出属于它自己的最优的 O b j ? Obj^* Obj? ,到底哪一种划分方式才是最后的划分方式?哪棵树的 O b j ? Obj* Obj? 值最小,那么就是最优的树。我们的目标就是找出 Obj 最小的一棵树,用作当前基学习器的决策树。
XGBoost 构建树的方法
- 精确贪婪算法
- 优化:近似算法
- 缺失值处理
- 学习率 shrinkage
树模型的学习策略
1. 穷举法
首先基于暴力方法把所有可能的决策树都计算一边,选择其中 Obj 值最小的那棵决策树。但是这种方法过于暴力,实际中无法应用。
总体的学习策略是:分步 + 贪心
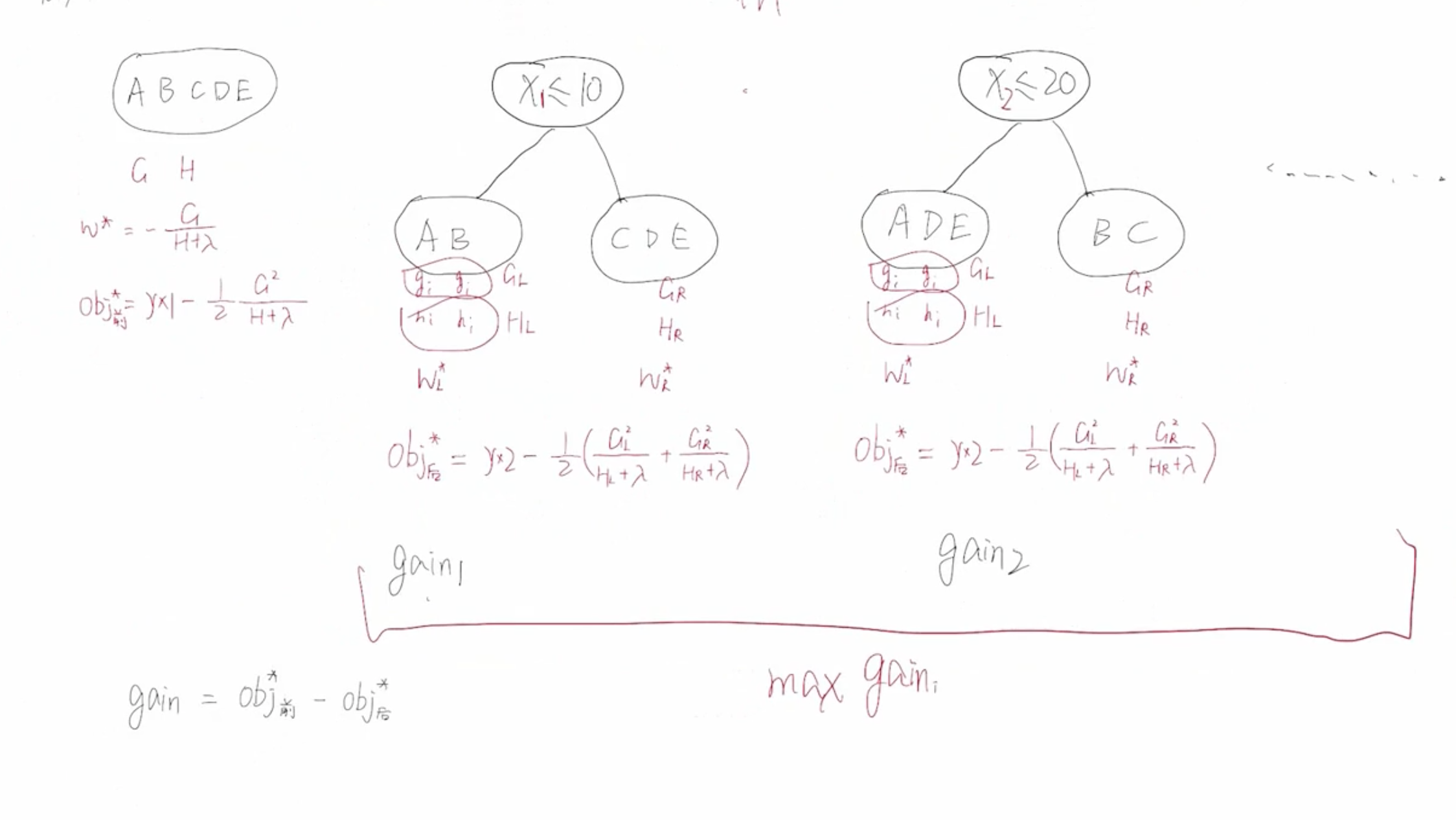
根据样本可以计算出 O b j 前 ? Obj_{前}^* Obj前?? 和 O b j 后 ? Obj_{后}^* Obj后?? 然后计算出增益:
G a i n = O b j 前 ? ? O b j 后 ? = 1 2 [ G L 2 H L + λ + G R 2 H R + λ ? ( G L + G R ) 2 H L + H R + λ ] ? γ Gain = Obj_{前}^* - Obj_{后}^* = \frac{1}{2}[\frac{G_L^2}{H_L + \lambda} + \frac{G_R^2}{H_R + \lambda} - \frac{(G_L + G_R)^2}{H_L + H_R + \lambda}] - \gamma Gain=Obj前???Obj后??=21?[HL?+λGL2??+HR?+λGR2???HL?+HR?+λ(GL?+GR?)2?]?γ
根据 G a i n Gain Gain 依次对每个节点进行分裂,何时停止节点分裂?
- 当 max Gain 小于等于 0 的时候就需要停止划分。
- 当叶节点包含的样本个数小于等于 1 的时候需要停止划分。
- 当树的深度达到阈值时停止划分。
优化:近似算法
-
压缩特征数
-
压缩
1. 压缩特征数
1.1 列采样
列采样是指对特征进行采样,比如有 3 个特征,从中随机抽取 2 个待用的特征。
1.1.1 按树随机
比如从 ( x 1 , x 2 , x 3 ) (x_1, x_2, x_3) (x1?,x2?,x3?) 这 3 个特征中选出 ( x 1 , x 2 ) (x_1, x_2) (x1?,x2?) 作为决策树划分依据,首先依次对 x 1 x_1 x1? 和 x 2 x_2 x2? 进行节点的划分,计算 G a i n Gain Gain, 选取 G a i n Gain Gain 值最大的划分方案作为根节点。然后,子节点的划分过程和根节点划分过程一样,始终只选择 ( x 1 , x 2 ) (x_1, x_2) (x1?,x2?) 这 2 个特征进行节点的划分。
总之,只要开始筛选出了某些特征作为划分依据,那么后面的每个子节点的划分都是按照开始选出来的特征进行划分。
1.1.2 按层随机
按层随机每次划分新节点的时候都会重新筛选特征,例如,随机选出了特征 ( x 1 , x 2 ) (x_1, x_2) (x1?,x2?) 对根节点进行划分。第二层,随机选出了特征 ( x 1 , x 3 ) (x_1, x_3) (x1?,x3?) 对第二层节点进行划分。每一层节点的划分都需要重新采样,每一层筛选出来的特征都可能是不一样的。
2. 压缩候选切分点数量
特征值分桶
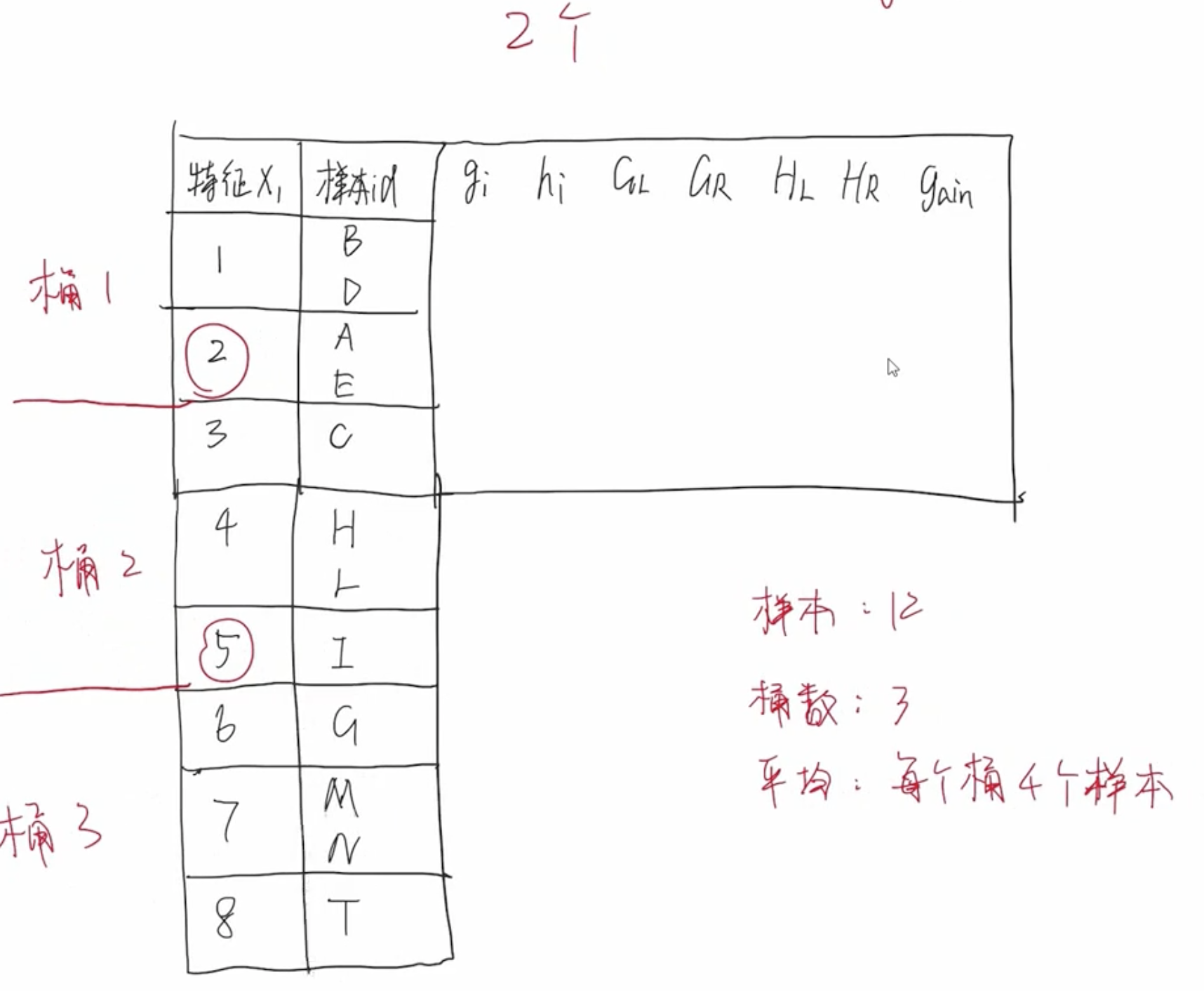
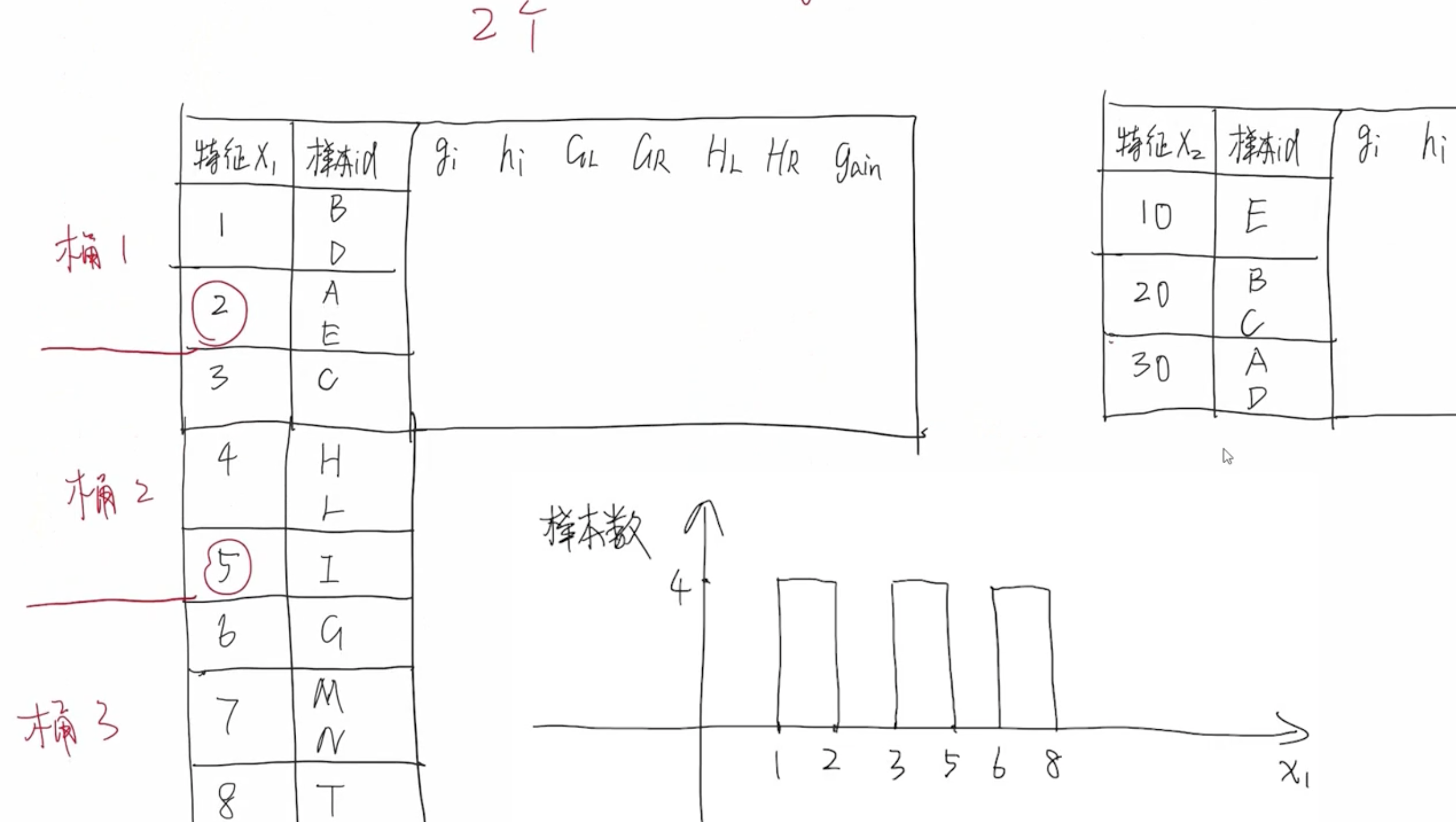
以上分桶方式过于理想化,它假设样本是均匀分布的,即每个桶中的样本数大致均匀。实际情况,每个样本的分布不是均匀的,有些样本数量比较多,有些样本数量比较少。因此,需要重新设计分桶策略。
2.1 加权分位法
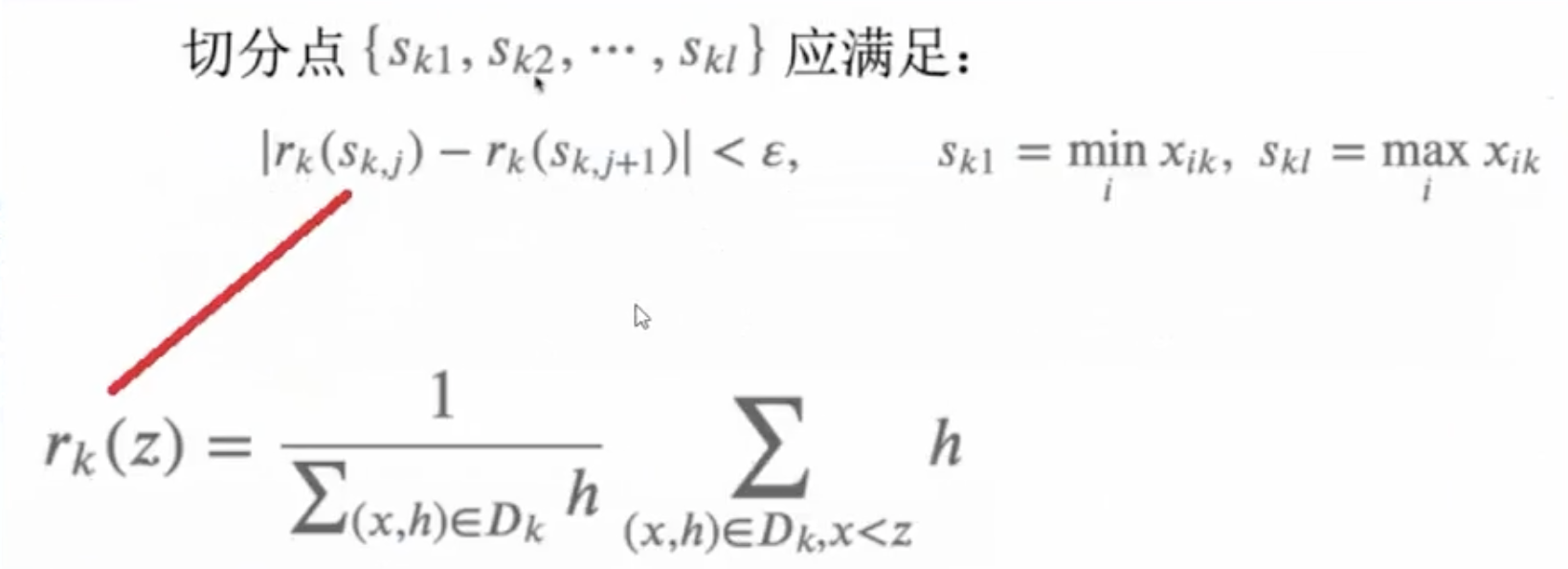
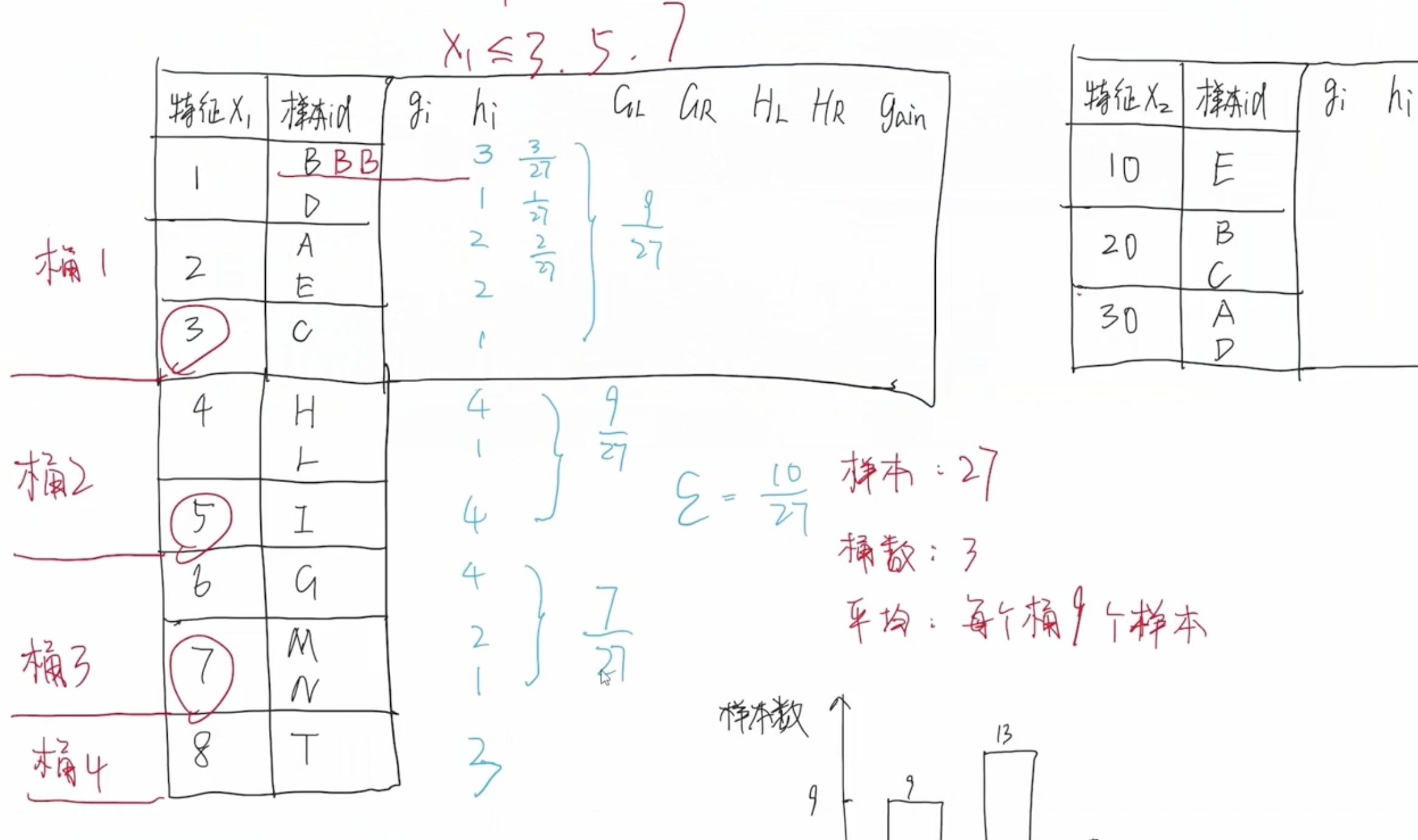
2.2 策略
2.2.1 全局策略
和 “按树随机” 思想类似,开始选定划分特征后,后面所有子节点的划分都按照这些特征进行。
2.2.2 局部策略
每个节点进行划分的时候,它所采样的这些特征都是不一样的,即每次都需要重新进行划分特征的采样。例如,根节点划分的时候采样到 ( x 3 , x 5 , x 7 ) (x_3, x_5, x_7) (x3?,x5?,x7?) ,对子节点的划分时,重新采样得到不同的特征。

从图中可以看出,局部策略 Test AUC 已经非常接近精确算法。
缺失值处理
Sparsity-aware Split Finding 稀疏自适应的划分点查找,它能对缺失值自动进行处理。
XGBoost 会将所有缺失值的样本当做一个整体看待,全部放到左节点计算 G a i n L Gain_L GainL?,全部放到右节点计算 G a i n R Gain_R GainR? 比较两者大小,根据 G a i n Gain Gain 值大小选择将全部缺失样本放到左右节点。
值得注意,当做排序和分位数算法的时候,缺失值是不参与排序和分位数计算的。
学习率 shrinkage
在 XGBoost 中也加入了步长 η \eta η,也叫做收缩率 shrinkage:
y i t ^ = y i ( t ? 1 ) ^ + η ?? f t ( x i ) \hat{y_i^t} = \hat{y_i^{(t-1)}} + \eta\;f_t(x_i) yit?^?=yi(t?1)?^?+ηft?(xi?)
这有助于防止过拟合,步长 η \eta η 通常取 0.1。
系统设计
- 核外块运算
- 分块并行
- 缓存优化
核外块运算
当数据集数量非常庞大以至于无法一次性加载到内存中,假设内存一次只能加载 2 条样本数据,剩下的那些没有办法加载到内存中的数据会以分块的形式存储到磁盘中。即无法一次性加载到内存中的数据会被划分成一块一块,分别存储到不同的磁盘中。这样在读取的时候就能够提高这个磁盘的吞吐率。
当内存中的数据计算完成后,就可以将磁盘中的数据加载到内存中。内存读写速度会远远快于磁盘读写速度,如果等内存中的数据完成计算后再加载磁盘中的数据到内存,那么必定会造成大量时间浪费,效率非常低。XGBoost 是如何处理这个问题?
XGBoost 单独开启一个线程来负责读取数据,即 CPU 在处理内存数据的同时,线程已经在读取磁盘中的样本数据到内存。这两个过程同步进行,避免 I/O 等待消耗大量时间。
磁盘块中存储的数据采用按列压缩算法,所以线程在读取磁盘中数据的时候,首先要进行解压缩的过程。
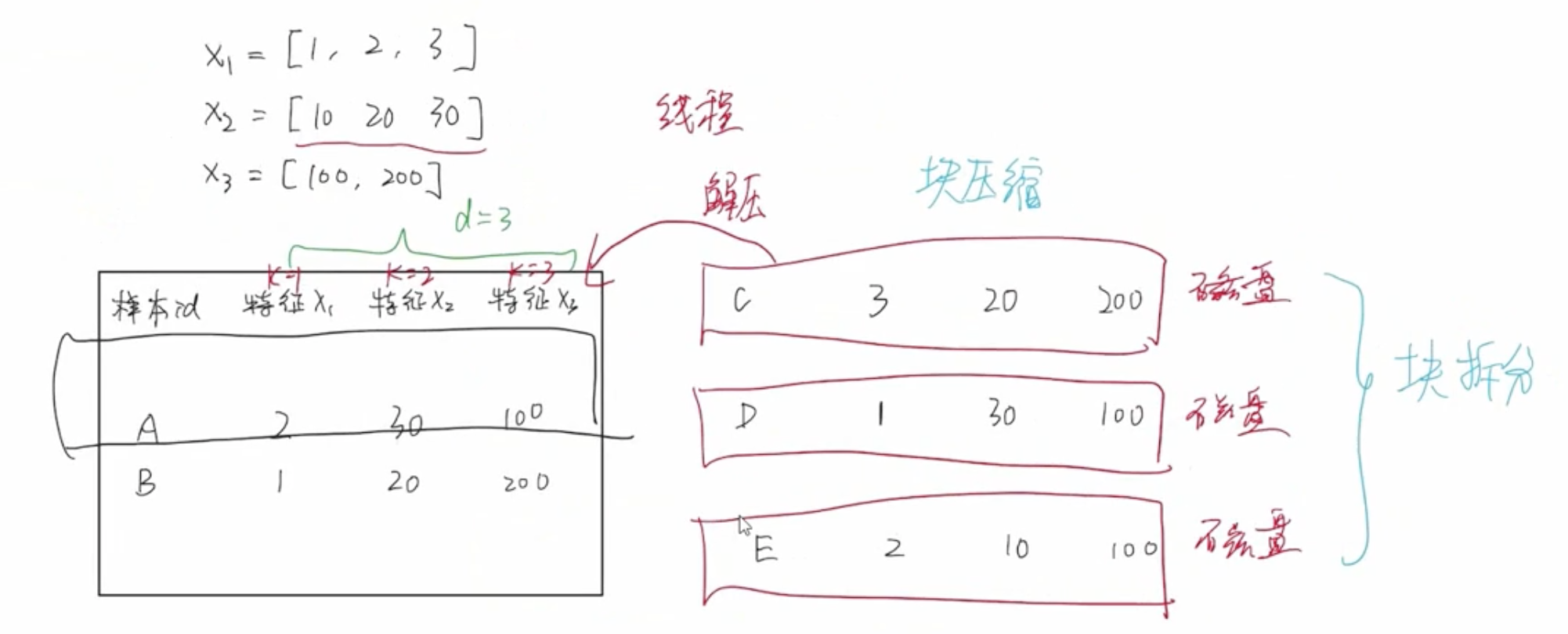
分块并行
分块并行是非常核心的设计,它让 XGBoost 能够实现分布式、并行化处理。
在构建回归树的过程中,最耗时的是排序操作。遍历每个特征的时候,都需要对特征值进行排序,可以通过减少特征值数量来加快树的构建速度。但是,尽管减少特征数量,排序仍然是一个非常耗时的操作。构建根节点的时候,需要排序。同时,在构建子节点的时候,仍然需要对子节点进行排序。所以,排序操作的时间消耗是不容忽视的。每个节点在计算 G a i n Gain Gain 的时候是互不影响、互不依赖的,意味着可以采用多线程同时计算按照不同特征进行节点划分时的 G a i n Gain Gain 值。
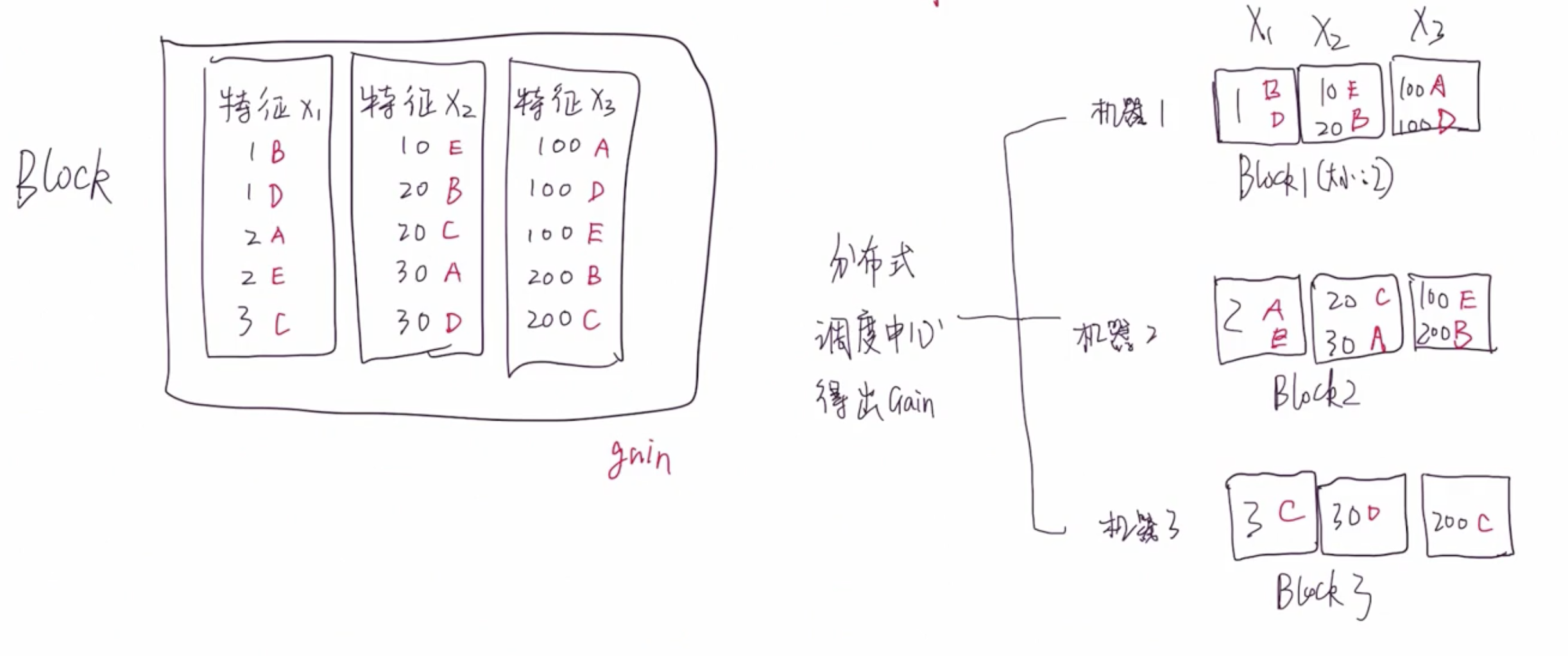
缓存优化
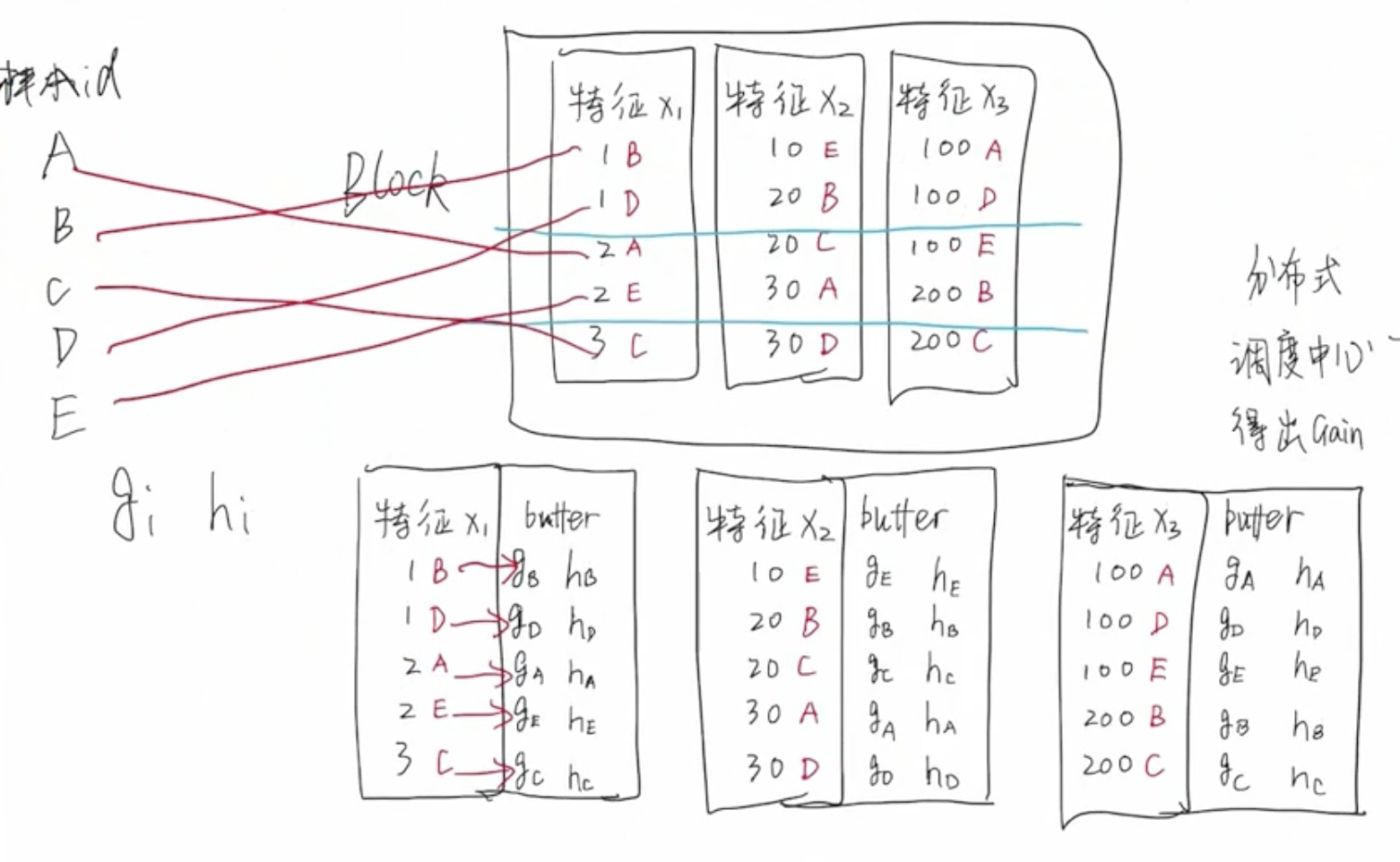
问题:Block 数据结构导致缓存命中率低
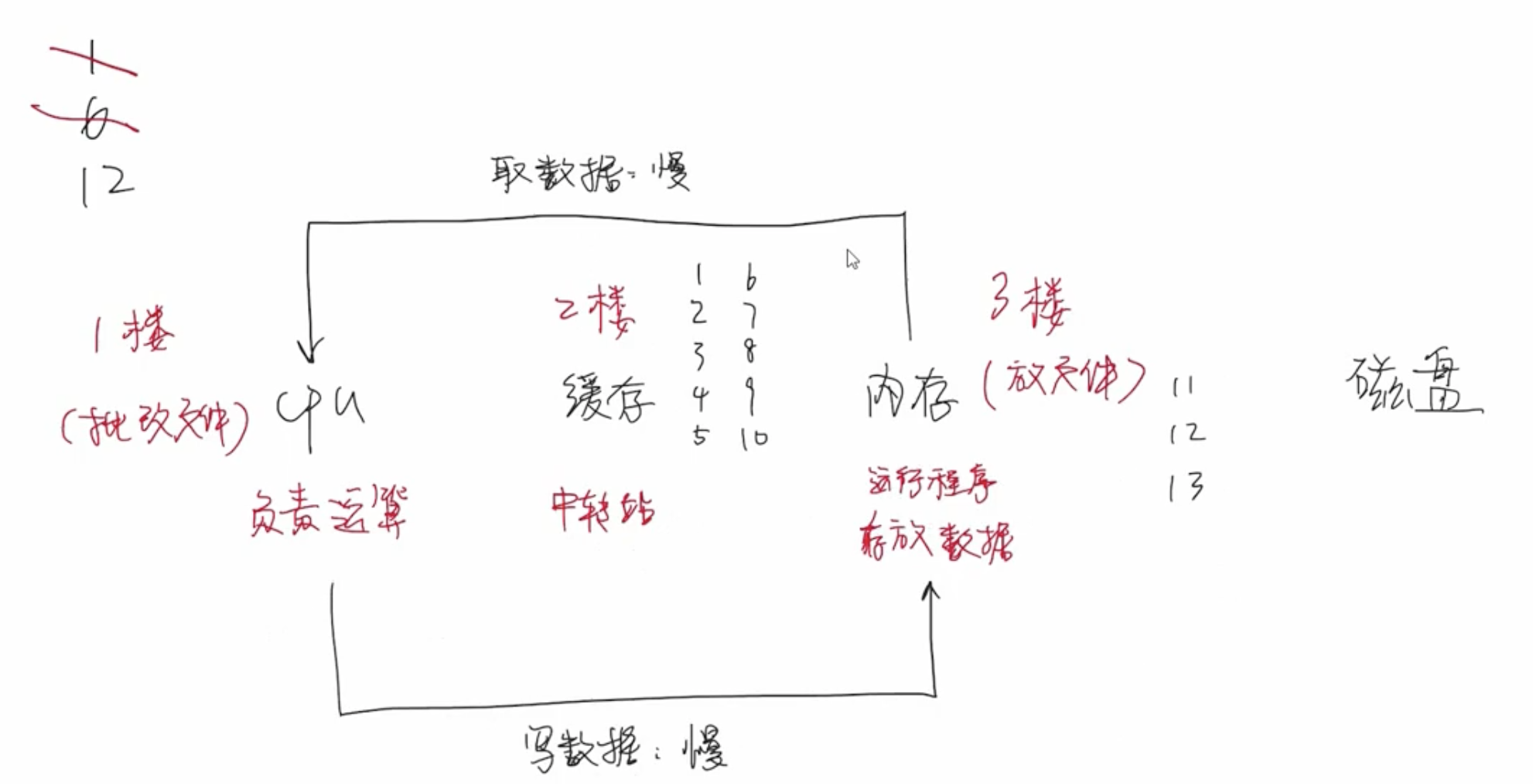
由于 Block 这种数据结构的限制,导致大量样本数据在内存中不是连续存储的,意味着缓存命中率会非常低,CPU 需要频繁地去内存中读取数据。
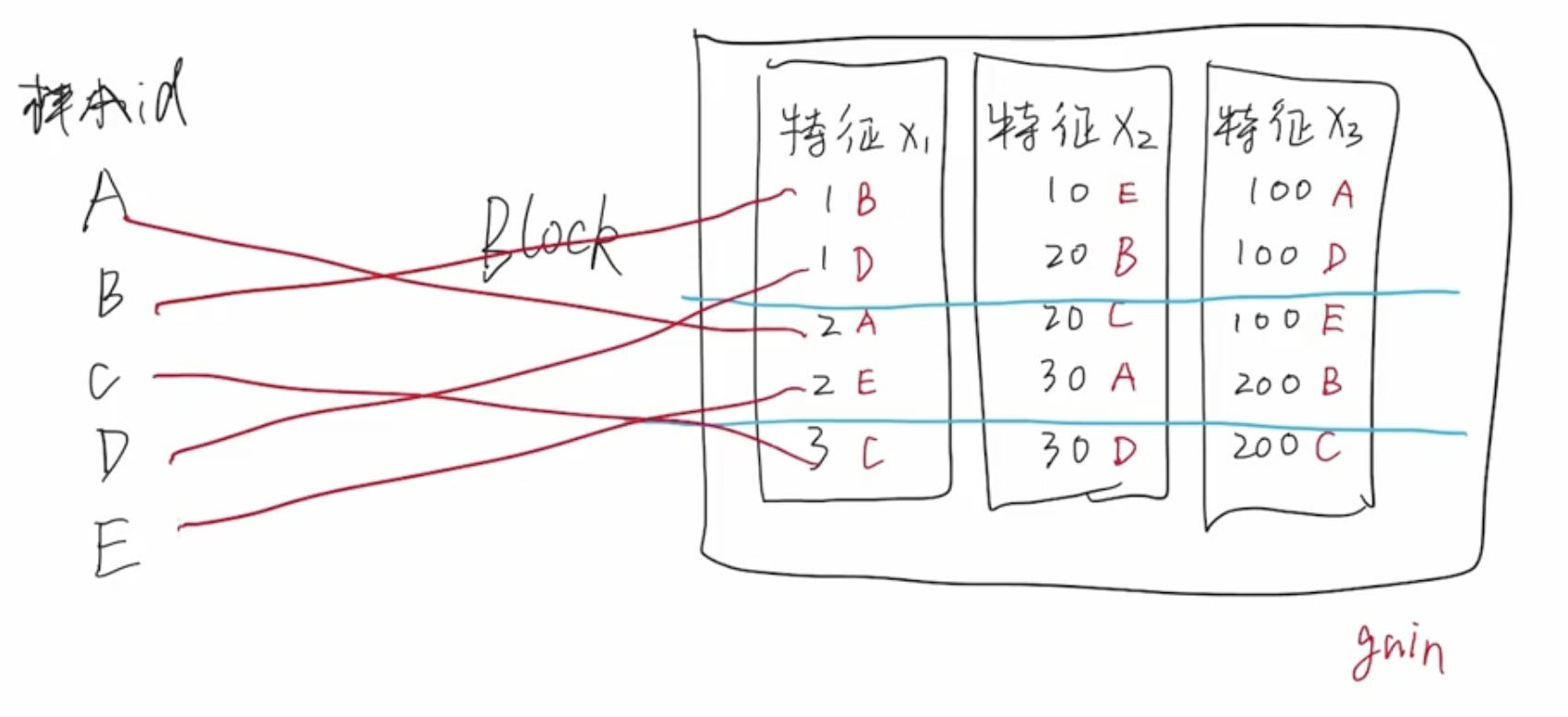
接下来介绍 XGBoost 是如何解决缓存命中率低的问题。
XGBoost 为每个 Block 中的特征列 x i x_i xi? 增加一个 buffer,这个 buffer 中存储着计算好的 g i g_i gi? 和 h i h_i hi? 的值。只需要在构建 Block 的时候进行一次非连续访问内存,计算出 g i g_i gi? 和 h i h_i hi? 后存储到 Block 结构中,这样后续进行节点划分和计算的时候,只需要顺序访问内存即可拿到全部信息,无需每次节点划分的过程都进行内存非连续访问。这样处理的好处,可以大大提高缓存命中率。