机动目标跟踪——匀加速运动模型(三维)
原创不易,路过的各位大佬请点个赞
WX: ZB823618313
机动目标跟踪——目标模型概述
1. 对机动目标跟踪的理解
??机动目标跟踪一直是目标跟踪领域研究的难点和重点问题。建立目标运动模型和滤波算法是目标跟踪的两个重要因素。由于目标的机动具有不可预测性,使得我们很难建立精确的目标运动模型。如何建立一种有效的模型来反映目标真实的运动轨迹是高机动目标跟踪系统急需解决的问题。经过近三十年的研究,该领域取得了许多重要成果。
个人理解:机动目标跟踪拥有三要素:
被跟踪目标建模(也是本博客重点)
传感器测量(另一个博客介绍)
滤波器设计(见目标跟踪专栏)
??从算法层面,在目标跟踪系统中,常用的滤波算法是以卡尔曼滤波器为基本框架的估计算法。卡尔曼滤波器是一种线性、无偏、以误差均方差最小为准则的最优估计算法,它有精确的数学形式和优良的使用效能。卡尔曼滤波方法实质上是一种数据处理方法,它采用递推滤波方法,根据获取的量测数据由递推方程递推给出新的状态估计。由于计算量和存储量小,比较容易满足实时计算的要求,在工程实践中得到广泛应用。
??除此之外,非线性滤波也广泛应用与机动目标跟踪,比如:
扩展卡尔曼滤波EKF
无迹卡尔曼滤波UKF
容积卡尔曼滤波CKF
求积卡尔曼滤波QKF
中心差分卡尔曼滤波CDKF
Divided difference filter DDF
高斯混合滤波GSF
强跟踪滤波STF
粒子滤波PF
… …
2. 目标模型概述
??机动目标模型描述了目标状态随着时间变化的过程。一个好的模型抵得上大量的数据。当前几乎所有的目标跟踪算法都是基于模型进行状态估计的。在卡尔曼滤波器被引入目标跟踪领域后,基于状态空间的机动目标建模成为主要研究对象之一。
目标的空间运动基于不同的运动轨迹和坐标系
一维运动
二维运动
三维运动(本博客主要讲匀加速三维目标)
下面三维匀加速运动CA模型:
3. 连续匀加速运动CA模型
为了方便,定义如下矩阵;
A
=
[
0
1
0
0
0
1
0
0
0
]
,
B
=
[
0
0
1
]
A=\begin{bmatrix}0&1&0\\0&0&1\\0&0&0\end{bmatrix}, B= \begin{bmatrix}0\\0\\1\end{bmatrix}
A=???000?100?010????,B=???001????
三维匀速运动模型(连续):
目标状态为:x维位置和速度加速度、y维位置速度加速度、z维位置速度加速度、即
X
=
[
x
,
x
˙
,
x
¨
,
y
,
y
˙
,
y
¨
,
z
,
z
˙
,
z
¨
]
T
{X}=[x, \dot{x},\ddot{x}, y, \dot{y},\ddot{y},z, \dot{z},\ddot{z} ]^T
X=[x,x˙,x¨,y,y˙?,y¨?,z,z˙,z¨]T
X ˙ ( t ) = [ A 0 0 0 A 0 0 0 A ] X ( t ) + [ B 0 0 0 B 0 0 0 B ] W ( t ) \dot{X}(t)=\begin{bmatrix}A&0&0\\0&A &0\\0&0&A\end{bmatrix}X(t) + \begin{bmatrix}B&0&0\\0&B&0\\0&0&B\end{bmatrix}W(t) X˙(t)=???A00?0A0?00A????X(t)+???B00?0B0?00B????W(t)
4. 离散匀加速运动CA模型(form 1)
为了方便,定义如下矩阵;
F = [ 1 T T 2 / 2 0 1 T 0 0 1 ] , G = [ T 2 / 2 T 1 ] F=\begin{bmatrix}1&T&T^2/2\\0&1&T\\0&0&1\end{bmatrix}, G= \begin{bmatrix}T^2/2\\T\\1\end{bmatrix} F=???100?T10?T2/2T1????,G=???T2/2T1????
离散化上述模型:
三维匀速运动模型(离散):
X
k
+
1
=
[
F
0
0
0
F
0
0
0
F
]
X
k
+
[
G
0
0
0
G
0
0
0
G
]
W
k
X_{k+1}=\begin{bmatrix}F&0&0\\0&F &0\\0&0&F\end{bmatrix}X_{k} + \begin{bmatrix}G&0&0\\0&G&0\\0&0&G\end{bmatrix}W_k
Xk+1?=???F00?0F0?00F????Xk?+???G00?0G0?00G????Wk?
白噪声
W
k
W_k
Wk?的方差为连续白噪声
W
(
t
)
W(t)
W(t)的功率谱强度
q
q
q。
5. 离散匀加速运动CA模型(form 2)
另一种三维匀加速运动模型为:
三维匀速运动模型(离散):
X
k
+
1
=
[
F
0
0
0
F
0
0
0
F
]
X
k
+
W
k
X_{k+1}=\begin{bmatrix}F&0&0\\0&F &0\\0&0&F\end{bmatrix}X_{k} + W_k
Xk+1?=???F00?0F0?00F????Xk?+Wk?
此时离散白噪声$W_k $方差为
Q
k
=
[
Q
0
0
0
Q
0
0
0
Q
]
Q_k=\begin{bmatrix}Q&0&0\\0&Q &0\\0&0&Q\end{bmatrix}
Qk?=???Q00?0Q0?00Q????
其中
Q
=
q
[
T
5
/
20
T
4
/
8
T
3
/
6
T
4
/
8
T
3
/
3
T
2
/
2
T
3
/
6
T
2
/
2
T
]
Q=q\begin{bmatrix}T^5/20&T^4/8&T^3/6\\T^4/8&T^3/3&T^2/2 \\ T^3/6& T^2/2 &T \end{bmatrix}
Q=q???T5/20T4/8T3/6?T4/8T3/3T2/2?T3/6T2/2T????
6. 匀加速运动CA模型Matlab实现
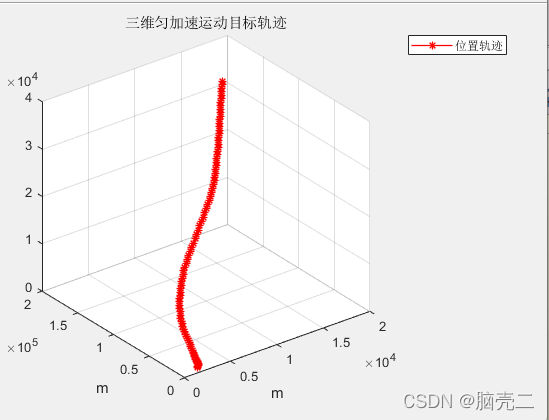
位置轨迹: 图1
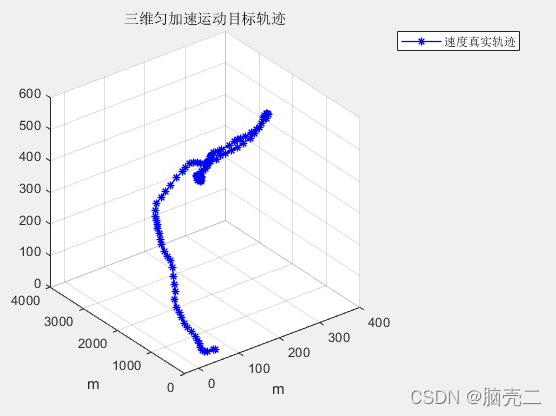
速度轨迹: 图2
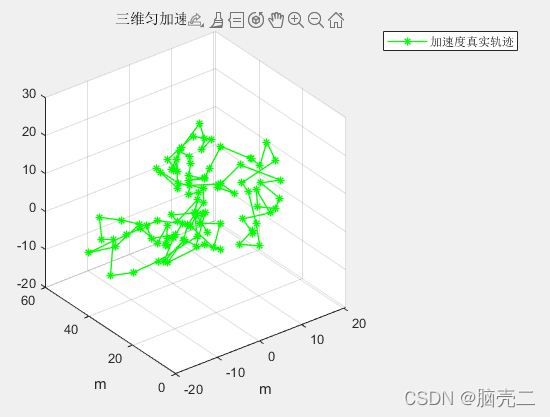
加速度轨迹: 图3
代码:
% cv 三维
clc;
clear all;
close all;
n=9; % state dimension : 0
T=1; % sample time.
N=100; %the runs atime,跟踪总时长
chan=1; %channel, 算法的个数,
w_mu=[0,0,0]';
v_mu=[0,0,0]';
%% target model
q=3; % 目标运动学标准差,过程噪声
Qk=q^2*eye(3);% cov. of process noise
Fk=[1,T,0,0,0,0;
0,1,0,0,0,0;
0,0,1,T,0,0;
0,0,0,1,0,0;
0,0,0,0,1,T;
0,0,0,0,0,1 ];
F=[1, T, T^2/2'; 0 1 T; 0 0 1];
Fk=blkdiag(F,F,F);
G=[ T^2/2;T;1];
Gk=blkdiag(G,G,G);
% % Gk=[ T^2/2, 0, 0;
% % T, 0, 0;
% % 0,T^2/2, 0;
% % 0, T, 0;
% % 0, 0,T^2/2;
% % 0, 0, T ];
%
%% define parameter
sV=zeros(n,N,1,1); % state
x=[1000,60,5,1000,60,10,1000,50,5]';%初始状态
P_0=diag([1e5,1e2,10, 1e5,1e2,10, 1e5,1e2,10]); %初始状态方差
%滤波器初始化
x0=mvnrnd(x,P_0); % 初始状态
%x0=(x+normrnd(0,0.001)')';
x=x0';
for k=1:N
%% %%%%%%% target model and measurement model%%%%%%%%%%%%%%%%%%%%
%% 目标运动学模型(被跟踪目标建模),匀速运动CV模型
w=mvnrnd(w_mu',Qk)';%过程噪声方差
x=Fk*x+Gk*w;
sV(:,k,1,1)=x;
end
% 三维匀速运动目标轨迹
figure
plot3(sV(1,:,1,1),sV(4,:,1,1),sV(7,:,1,1),'-*r','LineWidth',1);grid on
xlabel('m');ylabel('m');
legend('位置轨迹')
title('三维匀加速运动目标轨迹')
% 三维匀速运动目标轨迹
figure
plot3(sV(2,:,1,1),sV(5,:,1,1),sV(8,:,1,1),'-*b','LineWidth',1);grid on
xlabel('m');ylabel('m');
legend('速度真实轨迹')
title('三维匀加速运动目标轨迹')
% 三维匀速运动目标轨迹
figure
plot3(sV(3,:,1,1),sV(6,:,1,1),sV(9,:,1,1),'-*g','LineWidth',1);grid on
xlabel('m');ylabel('m');
legend('加速度真实轨迹')
title('三维匀加速运动目标轨迹')
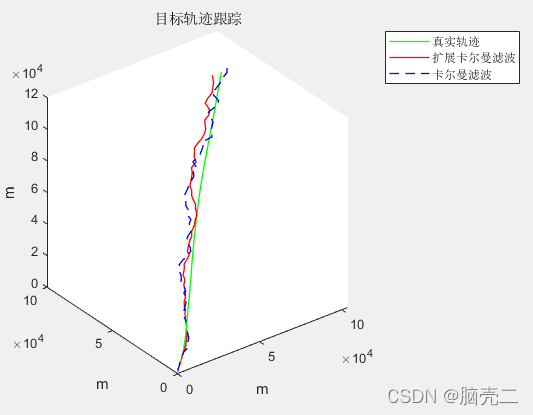
7. 卡尔曼和扩展卡尔曼滤波实现三维目标跟踪
算法:卡尔曼滤波、扩展卡尔曼滤波
传感器:雷达
跟踪代码:加微信:ZB823618313
两个场景:低精度,高精度
雷达量测模型
雷达量测为距离,方位角,俯仰角
r
k
m
=
r
k
+
r
~
k
b
k
m
=
b
k
+
b
~
k
e
k
m
=
e
k
+
e
~
k
{r}_k^m=r_k+\tilde{r}_k\\ b^m_k=b_k+\tilde{b}_k\\ e^m_k=e_k+\tilde{e}_k
rkm?=rk?+r~k?bkm?=bk?+b~k?ekm?=ek?+e~k?
其中
r
k
=
h
r
(
x
k
,
v
k
)
=
(
x
k
?
x
0
)
+
(
y
k
?
y
0
)
2
)
b
k
=
h
b
(
x
k
,
v
k
)
=
tan
?
?
1
y
k
?
y
0
x
k
?
x
0
e
k
=
h
e
(
x
k
,
v
k
)
=
tan
?
?
1
z
k
?
z
0
(
x
k
?
x
0
)
2
+
(
y
k
?
y
0
)
2
r_k=h_r(x_k,v_k)=\sqrt{(x_k-x_0)^+(y_k-y_0)^2)}\\ b_k=h_b(x_k,v_k)=\tan^{-1}{\frac{y_k-y_0}{x_k-x_0}}\\ e_k=h_e(x_k,v_k)=\tan^{-1}{\frac{z_k-z_0}{\sqrt{(x_k-x_0)^2+(y_k-y_0)^2}}}\\
rk?=hr?(xk?,vk?)=(xk??x0?)+(yk??y0?)2)?bk?=hb?(xk?,vk?)=tan?1xk??x0?yk??y0??ek?=he?(xk?,vk?)=tan?1(xk??x0?)2+(yk??y0?)2?zk??z0??
[
x
0
,
y
0
,
z
0
]
[x_0,y_0,z_0]
[x0?,y0?,z0?]为传感器(雷达)坐标,一般情况为0。雷达量测为
z
k
=
[
r
k
,
b
k
,
e
k
]
′
z_k=[r_k,b_k,e_k]'
zk?=[rk?,bk?,ek?]′。
跟踪轨迹图下图所示:
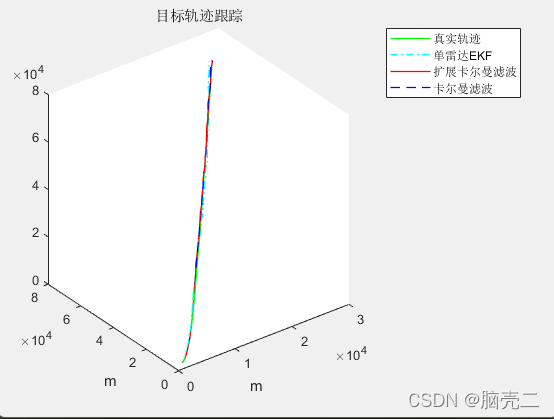
下面是跟踪RMSE曲线:评估跟踪精度
位置RMSE
速度RMSE


8. 其它模型
8.1 匀速转弯CT模型
匀速转弯CT运动模型见另一个博客:包括二维、三维
8.2. Singer模型
Singer模型见另一个博客
8.3. “当前”统计模型
当前统计模型见另一个博客
8.4. Jerk统计模型
Jerk模型见另一个博客
==原创不易,路过的各位大佬请点个赞=
