开发: C++知识库 Java知识库 JavaScript Python PHP知识库人工智能区块链大数据移动开发嵌入式开发工具数据结构与算法开发测试游戏开发网络协议系统运维
教程: HTML教程 CSS教程 JavaScript教程 Go语言教程 JQuery教程 VUE教程 VUE3教程 Bootstrap教程 SQL数据库教程 C语言教程 C++教程 Java教程 Python教程 Python3教程 C#教程
数码: 电脑笔记本显卡显示器固态硬盘硬盘耳机手机 iphone vivo oppo 小米华为单反装机图拉丁

-> 人工智能 -> 莫烦-pytorch -> 正文阅读

[人工智能]莫烦-pytorch

pytorch 莫烦

激励函数

Y = AF(Wx)
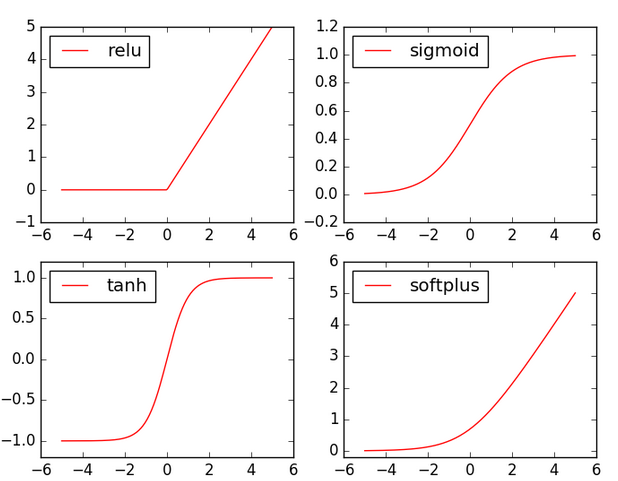
这里的AF()就是激励函数，其实就是另外一个非线性函数。比如relu，sigmoid，tanh

选择激励函数的窍门：当神经网络层只有两三层时，可选择任意的激励函数；当神经网络特别多层时，要慎重，小心梯度爆炸
CNN时推荐relu
RNN时推荐tanh或者relu

回归

建立神经网络

class Net(torch.nn.Module):  # 继承 torch 的 Module
    def __init__(self, n_feature, n_hidden, n_output):
        super(Net, self).__init__()     # 继承 __init__ 功能
        # 定义每层用什么样的形式
        self.hidden = torch.nn.Linear(n_feature, n_hidden)   # 隐藏层线性输出
        self.predict = torch.nn.Linear(n_hidden, n_output)   # 输出层线性输出

    def forward(self, x):   # 这同时也是 Module 中的 forward 功能
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.predict(x)             # 输出值
        return x

训练网络

# optimizer 是训练的工具,有四个常用的optimizer
optimizer = torch.optim.SGD(net.parameters(), lr=0.2)  # 传入 net 的所有参数, 学习率
loss_func = torch.nn.MSELoss()      # 预测值和真实值的误差计算公式 (均方差)

for t in range(100):
    prediction = net(x)     # 喂给 net 训练数据 x, 输出预测值

    loss = loss_func(prediction, y)     # 计算两者的误差

    optimizer.zero_grad()   # 清空上一步的残余更新参数值
    loss.backward()         # 误差反向传播, 计算参数更新值
    optimizer.step()        # 将参数更新值施加到 net 的 parameters 上

分类

建立神经网络

    def forward(self, x):
        # 正向传播输入值, 神经网络分析出输出值
        x = F.relu(self.hidden(x))      # 激励函数(隐藏层的线性值)
        x = self.out(x)                 # 输出值, 但是这个不是预测值, 预测值还需要再另外计算
        return x

训练网络

loss_func = torch.nn.CrossEntropyLoss()

快速搭建

搭建神经网络不止class net()这种方法，有一个快速的方法torch.nn.Sequential(）

net = torch.nn.Sequential(
    torch.nn.Linear(1, 10),
    torch.nn.ReLU(),
    torch.nn.Linear(10, 1)
)

Sequential方法直接认定的就是relu()这种激励函数，而对于自己手写的net来说，可以在forward()方法中指定激励函数，就会更加灵活一些。

保存与提取

保存

torch.save(net1, 'net.pkl')  # 保存整个网络
torch.save(net1.state_dict(), 'net_params.pkl')   # 只保存网络中的参数 (速度快, 占内存少)

提取

def restore_net():
    # restore entire net1 to net2
    net2 = torch.load('net.pkl')
    prediction = net2(x)

提取网络参数
网络参数：能独立地反映网络特性的参数
提取所有网路参数

net3.load_state_dict(torch.load('net_params.pkl'))
prediction = net3(x)

批训练

DataLoader

# 先转换成 torch 能识别的 Dataset
torch_dataset = Data.TensorDataset(data_tensor=x, target_tensor=y)

# 把 dataset 放入 DataLoader
loader = Data.DataLoader(
    dataset=torch_dataset,      # torch TensorDataset format
    batch_size=BATCH_SIZE,      # mini batch size.，就是每次取多少数据
    shuffle=True,               # 要不要打乱数据 (打乱比较好)
    num_workers=2,              # 多线程来读数据
)

优化器

要让神经网络聪明起来！！！！

SGD
Momentum
AdaGrad
RMSProp
Adam

SGD
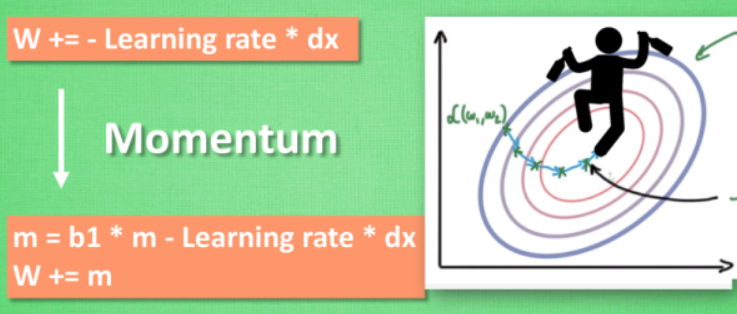
Momentum
所以我们把这个人从平地上放到了一个斜坡上, 只要他往下坡的方向走一点点, 由于向下的惯性, 他不自觉地就一直往下走, 走的弯路也变少了. 这就是 Momentum 参数更新.
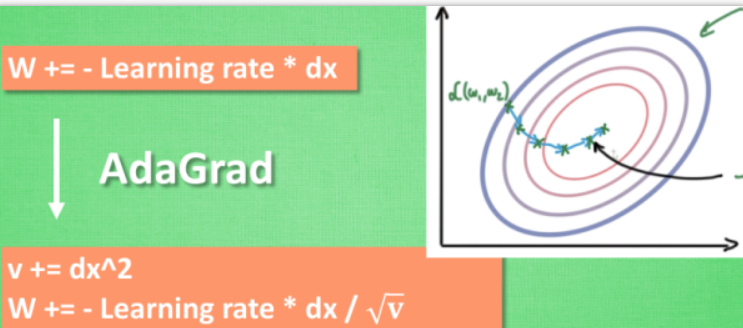
AdaGrad
而是给他一双不好走路的鞋子, 使得他一摇晃着走路就脚疼, 鞋子成为了走弯路的阻力, 逼着他往前直着走
RMSProp
是momentum和adagrad的集合体，同时具备两者的优势。但是RMSProp并没有包含momentum的一部分，所以在Adam中又进一步改进
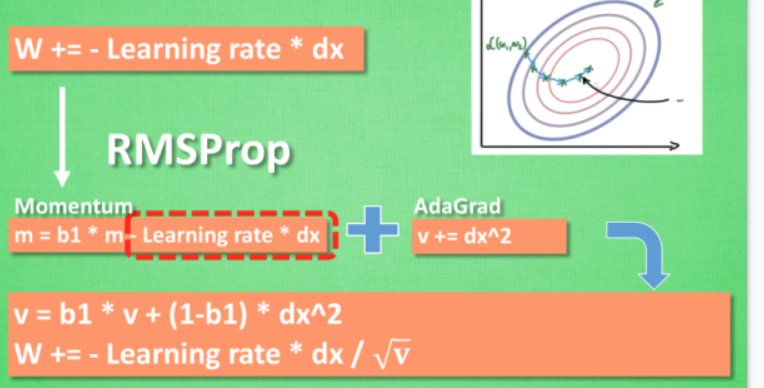
Adam
对于Adam来说，能快好的达到目标，快速收敛到最好的地方

Optimizer

SGD
Momentum
RMSProp
Adam

net_SGD         = Net()
net_Momentum    = Net()
net_RMSprop     = Net()
net_Adam        = Net()
# different optimizers
opt_SGD         = torch.optim.SGD(net_SGD.parameters(), lr=LR)
opt_Momentum    = torch.optim.SGD(net_Momentum.parameters(), lr=LR, momentum=0.8)
opt_RMSprop     = torch.optim.RMSprop(net_RMSprop.parameters(), lr=LR, alpha=0.9)
opt_Adam        = torch.optim.Adam(net_Adam.parameters(), lr=LR, betas=(0.9, 0.99))

在实验中，对各个优化器还是都应该试一试，看看哪个更好

CNN

1. 从下到上的顺序, 首先是输入的图片(image), 经过一层卷积层 (convolution), 然后在用池化(pooling)方式处理卷积的信息, 这里使用的是 max pooling 的方式.
2. 然后在经过一次同样的处理, 把得到的第二次处理的信息传入两层全连接的神经层 (fully connected),这也是一般的两层神经网络层,最后在接上一个分类器(classifier)进行分类预测. 这仅仅是对卷积神经网络在图片处理上一次简单的介绍.
1. 卷积层(Convolutional Layer) - 主要作用是提取特征
2. 池化层(Max Pooling Layer) - 主要作用是下采样(downsampling)，却不会损坏识别结果
3. 全连接层(Fully Connected Layer) - 主要作用是分类预测

class CNN(nn.Module):
    def __init__(self):
        super(CNN, self).__init__()
        self.conv1 = nn.Sequential(  # input shape (1, 28, 28)
            nn.Conv2d(
                in_channels=1,      # input height
                out_channels=16,    # n_filters
                kernel_size=5,      # filter size
                stride=1,           # filter movement/step
                padding=2,      # 如果想要 con2d 出来的图片长宽没有变化, padding=(kernel_size-1)/2 当 stride=1
            ),      # output shape (16, 28, 28)
            nn.ReLU(),    # activation
            nn.MaxPool2d(kernel_size=2),    # 在 2x2 空间里向下采样, output shape (16, 14, 14)
        )
        self.conv2 = nn.Sequential(  # input shape (16, 14, 14)
            nn.Conv2d(16, 32, 5, 1, 2),  # output shape (32, 14, 14)
            nn.ReLU(),  # activation
            nn.MaxPool2d(2),  # output shape (32, 7, 7)
        )
        self.out = nn.Linear(32 * 7 * 7, 10)   # fully connected layer, output 10 classes

    def forward(self, x):
        x = self.conv1(x)
        x = self.conv2(x)
        x = x.view(x.size(0), -1)   # 展平多维的卷积图成 (batch_size, 32 * 7 * 7)
        output = self.out(x)
        return output

这个 CNN 整体流程是卷积(Conv2d) -> 激励函数(ReLU) -> 池化, 向下采样 (MaxPooling) -> 再来一遍 -> 展平多维的卷积成的特征图 -> 接入全连接层 (Linear) -> 输出

RNN

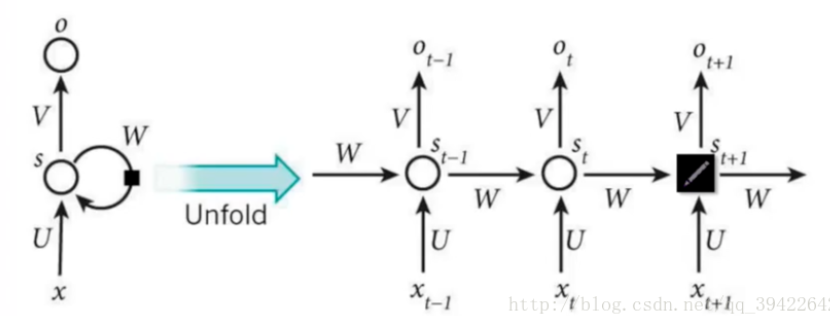
RNN是在有顺序的数据上进行学习的，在反向传递得到误差的时候，每一步都会乘以自己的一个参数W，若W是小于1，则误差传递到初始时间的时候会接近0，即梯度消失；反之，则是梯度爆炸！hong！然后LSTM是为了解决这个问题而提出来的

LSTM循环神经网络

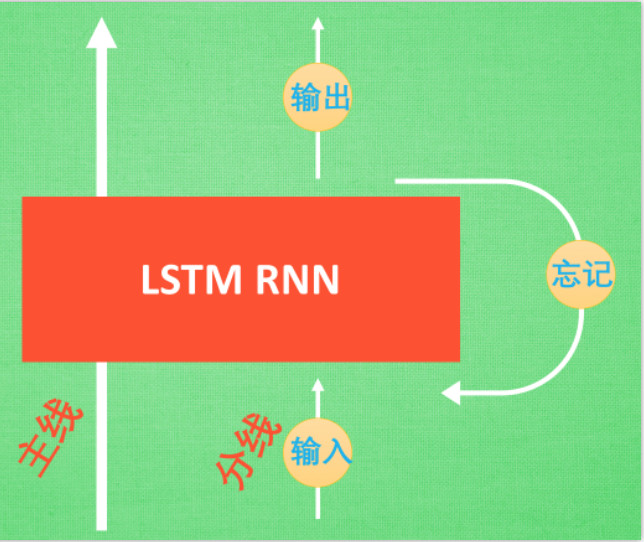
主线：就是主线剧情
分线，即是原本的RNN体系。
1. 输入：重要程度写入主线剧情进行分析.
2.忘记：如果此时的分线剧情更改了我们对之前剧情的想法, 那么忘记控制就会将之前的某些主线剧情忘记, 按比例替换成现在的新剧情
3.输出：基于目前的主线剧情和分线剧情判断要输出的到底是什么

RNN分类问题

class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.LSTM(     # LSTM 效果要比 nn.RNN() 好多了
            input_size=28,      # 图片每行的数据像素点
            hidden_size=64,     # rnn hidden unit
            num_layers=1,       # 有几层 RNN layers
            batch_first=True,   # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
        )

        self.out = nn.Linear(64, 10)    # 输出层

    def forward(self, x):
        # x shape (batch, time_step, input_size)
        # r_out shape (batch, time_step, output_size)
        # h_n shape (n_layers, batch, hidden_size)   LSTM 有两个 hidden states, h_n 是分线, h_c 是主线
        # h_c shape (n_layers, batch, hidden_size)
        r_out, (h_n, h_c) = self.rnn(x, None)   # None 表示 hidden state 会用全0的 state

        # 选取最后一个时间点的 r_out 输出
        # 这里 r_out[:, -1, :] 的值也是 h_n 的值
        out = self.out(r_out[:, -1, :])
        return out

RNN整体的流程是：

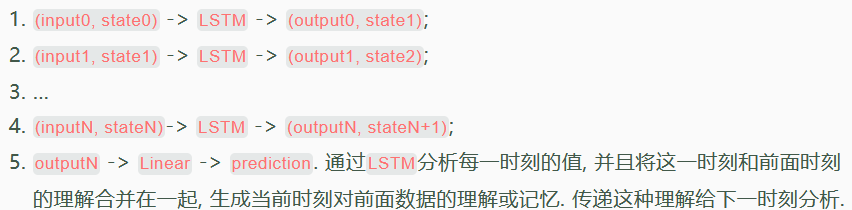
RNN回归问题

class RNN(nn.Module):
    def __init__(self):
        super(RNN, self).__init__()

        self.rnn = nn.RNN(  # 这回一个普通的 RNN 就能胜任
            input_size=1,
            hidden_size=32,     # rnn hidden unit
            num_layers=1,       # 有几层 RNN layers
            batch_first=True,   # input & output 会是以 batch size 为第一维度的特征集 e.g. (batch, time_step, input_size)
        )
        self.out = nn.Linear(32, 1)

    def forward(self, x, h_state):  # 因为 hidden state 是连续的, 所以我们要一直传递这一个 state
        # x (batch, time_step, input_size)
        # h_state (n_layers, batch, hidden_size)
        # r_out (batch, time_step, output_size)
        r_out, h_state = self.rnn(x, h_state)   # h_state 也要作为 RNN 的一个输入

        outs = []    # 保存所有时间点的预测值
        for time_step in range(r_out.size(1)):    # 对每一个时间点计算 output
            outs.append(self.out(r_out[:, time_step, :]))
        return torch.stack(outs, dim=1), h_state

自编码（Autoencoder）

是一种非监督式学习，接受大量的输入信息，然后总结原数据的精髓。
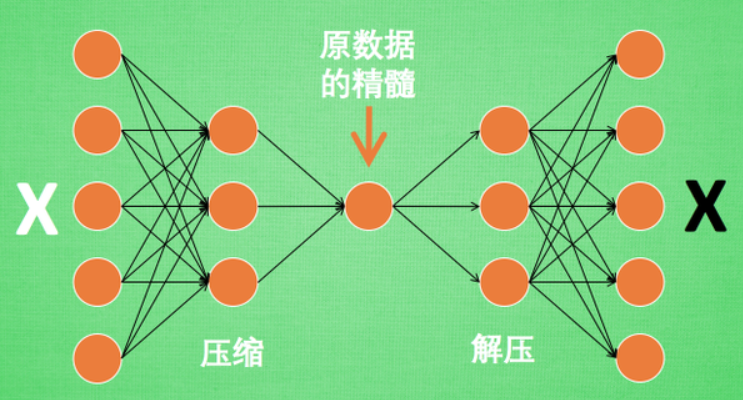
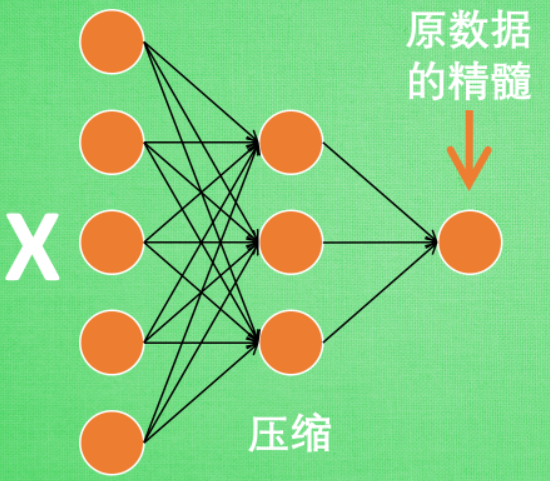
编码器Encoder
特征属性降维
解码器Decoder
将精髓信息解压成原始信息

AutoEncoder

class AutoEncoder(nn.Module):
    def __init__(self):
        super(AutoEncoder, self).__init__()

        # 压缩
        self.encoder = nn.Sequential(
            nn.Linear(28*28, 128),   28*28->128
            nn.Tanh(),
            nn.Linear(128, 64),   128->64
            nn.Tanh(),
            nn.Linear(64, 12),    64->12
            nn.Tanh(),
            nn.Linear(12, 3),   # 压缩成3个特征, 进行 3D 图像可视化
        )
        # 解压
        self.decoder = nn.Sequential(
            nn.Linear(3, 12),
            nn.Tanh(),
            nn.Linear(12, 64),
            nn.Tanh(),
            nn.Linear(64, 128),
            nn.Tanh(),
            nn.Linear(128, 28*28),
            nn.Sigmoid(),       # 激励函数让输出值在 (0, 1)
        )

    def forward(self, x):
        encoded = self.encoder(x)
        decoded = self.decoder(encoded)
        return encoded, decoded

autoencoder = AutoEncoder()

DQN

强化学习融合了神经网络+Q-learing

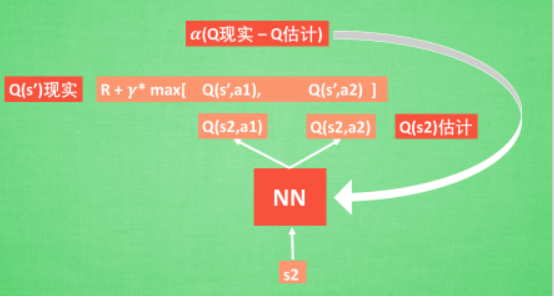
通过NN预测出Q(s2, a1) 和 Q(s2,a2) 的值，即Q估计
选取Q估计中最大值的动作来换取还清中的奖励reward
Q现实是之前在Q-learing中的值
更新神经网络中的参数

显示网络和估计网络建立的基本体系

class Net(nn.Module):
    def __init__(self, ):
        super(Net, self).__init__()
        self.fc1 = nn.Linear(N_STATES, 10)
        self.fc1.weight.data.normal_(0, 0.1)   # initialization
        self.out = nn.Linear(10, N_ACTIONS)
        self.out.weight.data.normal_(0, 0.1)   # initialization

    def forward(self, x):
        x = self.fc1(x)
        x = F.relu(x)
        actions_value = self.out(x)
        return actions_value

class DQN(object):
    def __init__(self):
        # 建立 target net 和 eval net 还有 memory

    def choose_action(self, x):
        # 根据环境观测值选择动作的机制
        return action

    def store_transition(self, s, a, r, s_):
        # 存储记忆
        #如果记忆满了，就覆盖老数据
    def learn(self):
        # target 网络更新
        # 学习记忆库中的记忆

GAN

大白话解释GAN：新手画家随机灵感画画，新手鉴赏家接受画作（不知道是新手画还是著名画），说出判断，一边还告诉新手怎么画，然后新手就画的越来越像著名画家的画。

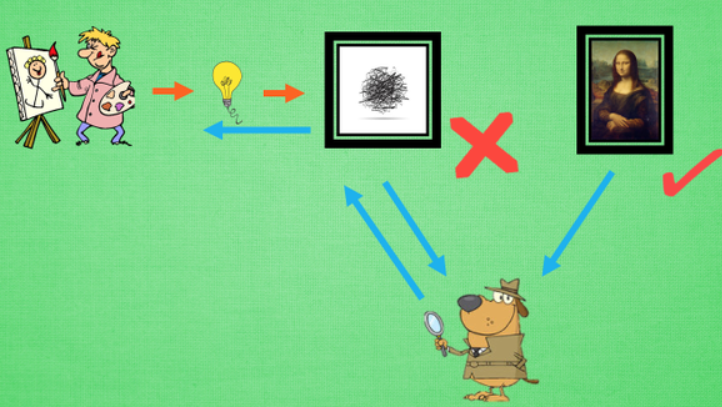
G = nn.Sequential(                      # Generator
    nn.Linear(N_IDEAS, 128),            # random ideas (could from normal distribution)
    nn.ReLU(),
    nn.Linear(128, ART_COMPONENTS),     # making a painting from these random ideas
)

D = nn.Sequential(                      # Discriminator
    nn.Linear(ART_COMPONENTS, 128),     # receive art work either from the famous artist or a newbie like G
    nn.ReLU(),
    nn.Linear(128, 1),
    nn.Sigmoid(),                       # tell the probability that the art work is made by artist
)

Dropout缓解过拟合

torch.nn.Dropout(0.5) 这里的 0.5 指的是随机有 50% 的神经元会被关闭/丢弃.

net_dropped = torch.nn.Sequential(
    torch.nn.Linear(1, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, N_HIDDEN),
    torch.nn.Dropout(0.5),  # drop 50% of the neuron
    torch.nn.ReLU(),
    torch.nn.Linear(N_HIDDEN, 1),
)

批标准化（Batch Normalization）BN

将分散的数据统一的一种做法，使数据具有统一规格。
BN被添加在每一个全连接和激励函数之间，对每一层神经网络进行标准化

class Net(nn.Module):
    def __init__(self, batch_normalization=False):
        super(Net, self).__init__()
        self.do_bn = batch_normalization
        self.fcs = []   # 太多层了, 我们用 for loop 建立
        self.bns = []
        self.bn_input = nn.BatchNorm1d(1, momentum=0.5)   # 给 input 的 BN

        for i in range(N_HIDDEN):               # 建层
            input_size = 1 if i == 0 else 10
            fc = nn.Linear(input_size, 10)
            setattr(self, 'fc%i' % i, fc)       # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
            self._set_init(fc)                  # 参数初始化
            self.fcs.append(fc)
            if self.do_bn:
                bn = nn.BatchNorm1d(10, momentum=0.5)
                setattr(self, 'bn%i' % i, bn)   # 注意! pytorch 一定要你将层信息变成 class 的属性! 我在这里花了2天时间发现了这个 bug
                self.bns.append(bn)

        self.predict = nn.Linear(10, 1)         # output layer
        self._set_init(self.predict)            # 参数初始化

    def _set_init(self, layer):     # 参数初始化
        init.normal_(layer.weight, mean=0., std=.1)
        init.constant_(layer.bias, B_INIT)

    def forward(self, x):
        pre_activation = [x]
        if self.do_bn: x = self.bn_input(x)    # 判断是否要加 BN
        layer_input = [x]
        for i in range(N_HIDDEN):
            x = self.fcs[i](x)
            pre_activation.append(x)    # 为之后出图
            if self.do_bn: x = self.bns[i](x)  # 判断是否要加 BN
            x = ACTIVATION(x)
            layer_input.append(x)       # 为之后出图
        out = self.predict(x)
        return out, layer_input, pre_activation

# 建立两个 net, 一个有 BN, 一个没有
nets = [Net(batch_normalization=False), Net(batch_normalization=True)]